KMS algorithm

The previous blog talked about bipartite graph matching匈牙利算法However, each matching edge weight in the Hungary algorithm is the same. If we get the best match under different matching edge weights, then we need to use the KM algorithm.

Basic principles

In fact, after we understand the Hungary algorithm, it is simple to understand the KM algorithm.

We now know that the Hungary algorithm can solve the problem of maximum matching, and now with weights, the KM algorithm is actually a way to convert the problem into a form that the Hungary algorithm can solve.

Now the bipartite graph has weights, which can be understood as adding a constraint. This constraint allows us to prioritize those edges with large weights for matching.

** Therefore, we need to pick out the edges with the largest weight first. In academic terms, it is to pick a subgraph. Because what we pick out are the edges with the largest weight, we only need to find the largest match in this subgraph, and this maximum match must be the one with the largest weight (very important, it means that in this subgraph, just look for the one with the largest weight on it, so we can use the Hungary algorithm to solve the problem) **. The process is:

Find the subgraph composed of the edges with the largest weight --------→ find the largest match on this subgraph

The above process is very simple, right? One problem is that we all find the edge with the largest weight to form a subgraph, which is very small and easy to conflict with. In terms of image, everyone’s requirements for finding a partner are too high, and it is very likely that they will not be able to meet their requirements. At this time, only some people can be wronged, let him lower his requirements a little, and let him choose a partner from other people.

The KM algorithm process, the core idea is: priority to choose the most satisfactory, because the requirements are too high to find the object of those people, reduce the standard to expand the range of mate selection, until the object is found.

In this problem, we can find the part with the largest match, and we can use the Hungary algorithm to solve it. The remaining two problems are:

1. How to find this so-called “most weighted subgraph”.

2. How to expand the range of mate selection. It can neither be too low nor not.

The above two problems are the essence of the KM algorithm.

The subgraph with the largest weight is the “equal subgraph”. Expanding the range of mate selection is the process of “updating the top data—establishing a new equal subgraph”.

It should be noted that the maximum weight mentioned above is not the greater the weight of the entire graph, the better, but the largest weight edge we can choose within the current ability range (after all, some people need to lower the standard to find the object).

First question

First of all, let’s emphasize that the purpose of our subgraph is to achieve an effect.

On this subplot, finding the maximum match without considering the weights is equivalent to finding the maximum match with the largest weight on the graph with weights.

We pick a group of people, these people are relatively high satisfaction with each other, those who are low will not be considered for the time being. Find a partner in this group. If you can’t find it, consider adding someone.

In order to achieve this goal, we add a top target to each person. We will not consider how this top target is added for now, and will talk about this issue in detail in the next step. Now assume that we already have a top target.

This top mark is the basis for us to decide whether an edge is added to the subgraph. The top mark can be understood as the highest standard for mate selection. If the degree of fit of both parties reaches this highest standard, it will be added to the mate selection range, that is, added to the subgraph.

Therefore, for example, the highest criterion for Xiao Wang’s mate selection is $S_ {Wang} $, and the highest criterion for Xiao Li’s mate selection is $S_ {li} $. The degree of liking of Xiao Wang and Xiao Li is W (that is, the connection weight of Xiao Wang and Xiao Li in the bipartite graph). If $W = S_ {Wang} + S_ {li} $is added to the subgraph and enters the range of mate candidates. Noting the above equation, the subgraph selected in this way is called an equal subgraph.

However, this highest standard is constantly changing. That is the next question, how to constantly adjust the highest standard so that the range of mate selection is constantly changing.

Second question

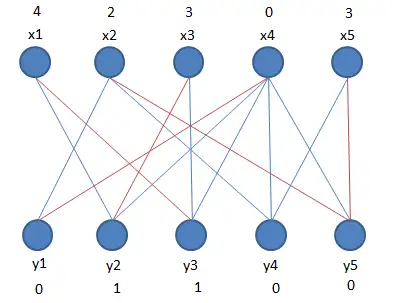
Let’s take a specific example here.

Here are 5 girls x1-x5 and 5 boys y1-y5. 0 between them means there is no connection, and numbers greater than 0 are weights, which is how much they like each other.

$$\begin{bmatrix} & y1 & y2 & y3 & y4 & y5 \\ x1 & 3 & 5 & 5 & 4 & 1 \\ x2 & 2 & 2 & 0 & 2 & 2 \\ x3 & 2 & 4 & 4 & 1 & 0 \\ x4 & 0 & 1 & 1 & 0 & 0 \\ x5 & 1 & 2 & 1 & 3 & 3 \end{bmatrix}$$

** The first step, the highest standard initialization. **

It should be noted that we are an undirected bipartite graph, which means that the weight is the common liking degree of both parties, so you can choose one person as the representative. So, we let the girls make a unilateral choice.

So the boys’ top bar is set to 0.

In the beginning, girls wanted to find their favorite partner, and we set their highest standard to the one they liked the most. For example, x1 is interested in all boys, and the degree of liking is 3, 5, 5, 4, 1. So her current highest standard is 5.

In the first selection, y2 and y3 will be added to the mate selection range, and the other three will not be considered for the time being. All girls are like this, choose their favorite to join the mate selection range.

We get the subgraph

The advantage of this is that in the subgraphs picked out in this way, the degree of liking each other must be the greatest. In this way, we don’t have to consider the weight problem, and the problem becomes a problem of picking the largest match on the local subgraph, which can be solved with the Hungary algorithm.

When we reach this point, we cannot continue to find the expansion path. At this time, we need to expand the scope of mate selection

** The second step, the highest standard adjustment. **

We randomly choose an alternate path that does not go down above (because we did not successfully find another unmatched object, this alternate path is not qualified to be called an augmentation path). For example, choose this one:

x4----y2----x3----y3------x1----y2----???

This route is also called an alternate tree in many articles. Once the augmentation path is found, we can expand the matching range and find objects for x4 as well. But now it has failed, and the essence of this failure is a conflict with the person on the route. 2

So let’s see who is involved in the failure of x4. Girls: x1, x3, x4. Boys: y2, y3.

Now we have to coordinate the highest standards of these people’s mate selection (that is, their top standards) and expand the scope of mate selection.

First of all, we can’t destroy the original relationship. The original top standard is designed to ensure that you can choose your favorite object. So it is necessary to ensure that the highest standard between them remains unchanged, so as to ensure that the original match will not change.

Here let the above conflict with the x4 of these people: the top of the girls decreased, the top of the boys increased, so that their combined standard unchanged.

However, the top mark for girls is reduced, and opportunities for others come.

Going back to the formula of our picker diagram just now, it is the equation of Xiao Wang and Xiao Li.

Now Xiao Wang has lowered the standard because of conflicts with others, and W has been reduced, that is, some edges with less weight have the opportunity to be added to the subgraph now.

Now girls: x1, x3, and x4 all like y2 and y3, and they have a conflict, but y1, y4, and y5 have not been considered by them. Originally, the standard of x1 was 5, but now that she wants to consider y1, the weight of x1y1 is 3, and she needs to lower the standard by 2.

Similarly, x1y4 needs to be reduced by 1; x3y1 needs to be reduced by 2, x3y4 needs to be reduced by 4-1 = 3; x3y5 needs to be reduced by 4-0 = 4. x4 is the same algorithm.

Therefore, considering the maximum weight, at least one standard should be reduced.

Therefore, we put the standard -1, y2, and y3 of x1, x3, and x4 corresponding to + 1.

** Under this criterion, we still have to pick the edge that satisfies “two-person top mark and = two-person connection weight”. **

It can be seen that after x4 colleagues lowered their standards, all male colleagues met her standards.

At this point we can find a perfect match for this graph,