Performance and Principle of Universal Lock

Posted on Edited on In Waline:

This time, we must deal with what a universal lock is. This article will slowly unfold in the following order:

  • Through a simple practical example to tell you, the performance of the universal lock in our lives
  • What’s a universal lock?
  • Talk about the principle of the existence of universal locks from the perspective of matrices and geometry respectively
  • What’s wrong with the universal lock?
  • Why quaternions can solve the gimbal lock problem

A small experiment with a universal lock

You can take out the phone and put it on the desktop, the screen is facing up, the longest side of the phone is perpendicular to the edge of the table is set to the X axis, and the short side of the screen is parallel to the edge of the table is set to the Y axis, so the vector between the vertical and the screen is the Z axis.

We first rotate 30 degrees clockwise around the X axis of the longest side of the mobile phone. At this time, the mobile phone leaves the desktop, leaving a long side in contact with the table; then rotate 90 degrees around the Y axis, that is, the short side of the mobile phone, so that the screen surface is connected with the table. Parallel to the edge;

Rotate 10 degrees around the Z axis, that is, rotate 10 degrees around the axis perpendicular to the screen. At this time, you will find that when you rotate around the Z axis, the screen surface is still parallel to the edge of the table, and the angle of rotation around the Z axis at this time gives The effect of the phone’s posture is the same as the initial rotation of the X axis on the phone’s posture - both make the final posture of the phone (which has been rotated 90 degrees around the Y axis so that the phone screen is parallel to the edge of the table) rotate a certain angle around an axis perpendicular to the screen.

In other words, you can not rotate around the Z axis, by adjusting the number of angles around the X axis, so that the final attitude of the phone and the rotation process to achieve the same attitude.

In other words, once the Y axis is rotated 90 degrees, your phone plane must be in a plane perpendicular to the desktop, no matter how you start with the X axis and end with the Z axis

Universal lock

What is Euler’s Angle?

Let’s briefly talk about Euler’s angle before explaining the universal lock.

We have actually been exposed to this concept, but it may not be that deep, so let’s explain it here:

Leonhard Euler used Euler angles to describe the orientation of a rigid body in three-dimensional Euclidean space. For any reference frame, the orientation of a rigid body is set by rotating three Euler angles from the reference frame in order. Therefore, the orientation of a rigid body can be determined by three basic rotation matrices. In other words, any rotation matrix about the rotation of a rigid body is composed of three basic rotation matrices.

It is divided into static Euler angles and dynamic Euler angles

Static: that is, the rotation around the three axes of the world coordinate system, because the coordinate axis remains static during the rotation of the object, it is called static.

2, dynamic: that is, the rotation around the three axes of the object coordinate system, because the coordinate axis of the object rotates with the object to do the same rotation, so called dynamic.

Static euler angle

For a reference system in three-dimensional space, the orientation of any coordinate system can be represented by three Euler angles. The reference system (fixed system), also known as the laboratory reference system, is stationary. The coordinate system (solid connection) is fixed to the rigid body and rotates as the rigid body rotates.

See the figure on the right. Set the xyz-axis as the reference axis of the reference system. The intersection of the xy-plane and the XY-plane is called the intersection line, represented by the English letter (N). The Euler angle of zxz cis can be statically defined as follows:

  • $\ alpha $ (precession angle) is the angle between the x-axis and the intersection line,
  • $\ beta $ (nutation angle) is the angle between the z-axis and the Z-axis,
  • $\ gamma $ (spin angle) is the angle between the intersection line and the X-axis.

There is no convention for the order and marking of the included angles, the designation of the two axes of the included angles. Scientists have never reached a consensus on this. Whenever Euler angles are used, we must clearly indicate the order of the included angles and specify their reference axes.

Range of angular values

The $\ alpha $and $\ gamma $values range from 0 to 2 dollars\ piradians,respectively.radians, respectively.\ Beta $values are radians from 0 to $\ pi $.
The set of Euler angles is unique for each orientation; with some exceptions:

If the $\ alpha $of two Euler angles, one is 0 and the other is 2 dollars\ pi $, and $\ beta $and $\ gamma $are equal, then both Euler angles describe the same orientation.
If $\ gamma $of two Euler angles, one is 0 and the other is 2 dollars\ pi $, and $\ alpha $and $\ beta $are equal, then both Euler angles describe the same orientation.

As mentioned earlier, the rotation matrix {\ displaystyle [\ mathbf {R}]} [\ mathbf {R}] with the rigid body orientation is composed of three basic rotation matrices:

[R]=[cosγsinγ0−sinγcosγ0001][1000cosβsinβ0−sinβcosβ][cosαsinα0−sinαcosα0001][R] = \begin{bmatrix} cos\gamma & sin\gamma & 0 \\ -sin\gamma & cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\beta & sin\beta \\ 0 & -sin\beta & cos\beta \end{bmatrix} \begin{bmatrix} cos\alpha & sin\alpha & 0 \\ -sin\alpha & cos\alpha & 0 \\ 0 & 0 & 1 \end{bmatrix}

The result after the calculation is

[R]=[cosαcosγ−cosβsinαsinγsinαcosγ+cosβcosαsinγsinβsinγ−cosαsinγ−cosβsinαcosγ−sinαsinγ+cosβcosαcosγsinβcosγsinβsinα−sinβcosαcosβ][R] = \begin{bmatrix} cos\alpha cos\gamma - cos\beta sin\alpha sin\gamma & sin\alpha cos\gamma + cos\beta cos\alpha sin\gamma & sin\beta sin\gamma \\ -cos\alpha sin\gamma - cos\beta sin\alpha cos\gamma & -sin\alpha sin\gamma + cos\beta cos\alpha cos\gamma & sin\beta cos\gamma \\ sin\beta sin\alpha & -sin\beta cos\alpha & cos\beta \end{bmatrix}

In classical mechanics, the Euler angle is often set by the zxz conformism; according to the axis name of the second axis of rotation, it is abbreviated as the x-conformism. In addition, there are other types of Euler angle groups. In a legal Euler angle group, the only restriction is that any two consecutive rotations must rotate around different axes of rotation. Therefore, there are a total of 12 conformities. For example, y-conformism, where the second axis of rotation is the y-axis, is commonly used in quantum mechanics, nuclear physics, and particle physics. In addition, there is a compliance, xyz conformism, used in aerospace engineering; see Tate-Bryan angle

Dynamic Euler angle

We can also give two different dynamic definitions of the Euler angle. One is a composite of three rotations around a coordinate axis fixed to a rigid body; the other is a composite of three rotations around a laboratory reference axis. With a dynamic definition, we can better understand the physical meaning and application of the Euler angle. Note in particular that, in the following description, the XYZ coordinate axis is the rotating rigid body coordinate axis; while the xyz coordinate axis is the stationary laboratory reference axis.

  • Rotation around the XYZ axis: Initially, the axes of both coordinate systems xyz and XYZ overlap. Start by rotating $\ alpha $, the angular value, around the Z-axis. Then, rotate $\ beta $, the angular value, around the X-axis. Finally, rotate $\ gamma $, the angular value around the Z-axis.

  • Rotation around the xyz axis: Initially, the axes of both coordinate systems xyz and XYZ overlap. Start by rotating $\ gamma $, the angular value, around the z-axis. Then, rotate $\ beta $, the angular value, around the x-axis. Finally, rotate $\ alpha $, the angular value around the z-axis.

What is a universal lock?

We learned that Euler angles are divided into static Euler angles and dynamic Euler angles, and we continue to see what a universal lock is.

First of all, let’s intuitively understand that the universal lock will only produce dynamic Euler angles, that is, we are rotating around the object’s own coordinate system, and the object’s own coordinate system will rotate with the object’s rotation

Through the above small experiment, we can roughly understand that the reason why the universal lock is called a lock is because the rotation effect of two dimensions overlaps, that is, the effect of rotating the X axis and can be achieved by rotating the Z axis, that is, a dimension is lost.

But from another point of view, this “lock” does not mean that there are any angles that cannot be expressed in the Euler angle, but that if your nutation angle is 90 degrees, your final result must be in a certain plane.

The principle of universal lock

Geometrically speaking

Let’s first take a look at the following graph. The coordinate system of this graph is both the object’s own coordinate axis, which is exactly the same as the world coordinate axis

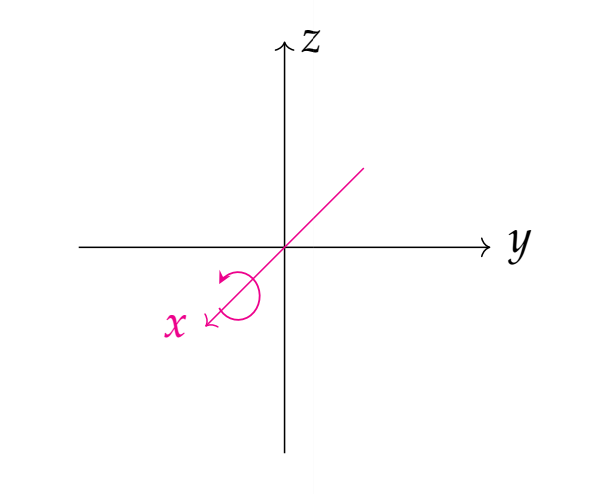
Let’s first rotate an angle around the x-axis, no problem

Then we rotate 90 degrees around the y-axis

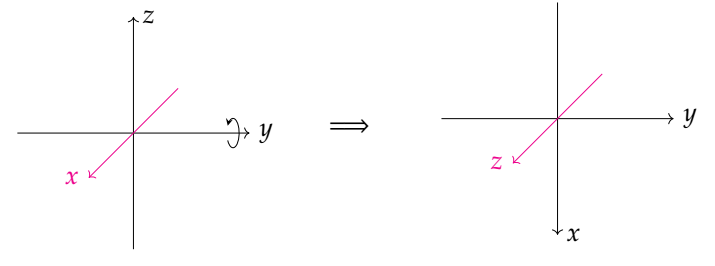
At this time, you can see that the z-axis has changed to the direction of the original x-axis. At this time, we rotate around the z-axis of the object itself. From the perspective of world coordinates, it is about the x-axis of the initial state, that is to say, from the perspective of the world coordinate system. From the point of view, it seems that the x-axis of the object itself at the beginning and the z-axis of the object itself at the end are the same, both of which revolve around the x-axis of the world coordinate system

From a matrix perspective

The above process is written in the form of matrix multiplication

Rz(β)Ry(π/2)Rx(α)=[cosβ−sinβ0sinβcosβ0001][001010−100][1000cosα−sinα0sinαcosα]=[0sin(α−β)cos(α−β)0con(α−β)−sin(α−β)−100]=[001010−100][1000cos(α−β)−sin(α−β)0sin(α−β)cos(α−β)]=Ry(π/2)Rx(α−β)R_z(\beta)R_y(\pi / 2)R_x(\alpha) \\ =\begin{bmatrix} cos\beta & -sin\beta & 0 \\ sin\beta & cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha \\ 0 & sin\alpha & cos\alpha \end{bmatrix} \\ = \begin{bmatrix} 0 & sin(\alpha - \beta) & cos(\alpha - \beta) \\ 0 & con(\alpha - \beta) & -sin(\alpha - \beta) \\ -1 & 0 & 0 \end{bmatrix} \\ = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha - \beta) & -sin(\alpha - \beta) \\ 0 & sin(\alpha - \beta) & cos(\alpha - \beta) \end{bmatrix} \\ = R_y(\pi /2)R_x(\alpha - \beta)

What’s wrong with the universal lock?

So the universal lock is not unable to represent a certain angular displacement in space, but because of the universal lock, the interpolation between angular displacements becomes unsatisfactory, so how does the universal lock appear? When the second rotation angle is 90 degrees, use the first axis to coincide with the third axis. This is to understand this phenomenon from a perceptual point of view. If it is explained from a mathematical point of view, it is cos90 = 0

In the game, when the animation of the character rotation is triggered, the character will make a series of continuous rotation transformations, each transformation must be represented by a set of Euler angles, but it is impossible to store the Euler angles of each orientation. So the animator defines a series of key frames, specifying the position of the character at the key frame (described by a set of Euler angles), and then the computer interpolates these sets of Euler angles according to time t to obtain a series of Euler angles.

If the pitch is not ± 90 °, there will be no gimbal lock phenomenon, and a series of Euler angles after interpolation can completely characterize the desired character rotation path.

If the pitch of a key frame, that is, the rotation around the second axis, is 90 °, you will encounter a universal lock. At this time, the phone can only rotate in a horizontal plane. If the animator specifies that the orientation of the next key frame phone is not standing up, there is no problem, but what happens if the orientation of the next key frame specified is standing up?

How Quaternions Solve the Gimbal Lock Problem

Another way to represent rotation

To solve this problem, we must first ask about the preconditions for the existence of the universal lock problem

As we know earlier, the universal lock only exists in the dynamic Euler angle, that is, the object rotates around its own coordinate system, and its own coordinate system rotates with its own rotation. If it rotates 90 degrees on the Y axis, the X axis and Z axis The rotation effect of the axis is the same.

Think about it from another angle, in fact, under the Euler angle, the same effect has many different rotation methods, resulting in uncertain interpolation results.

To solve this problem, in fact, the idea is relatively clear, that is, change the representation method, in this new representation method, the representation method of a rotation result is unique.

We give another way to express the direction: Axis-Angle-Representation. Unlike Euler angles, this time we don’t take multiple rotations to find the target direction, but instead find an axis of rotation, and we can get the target direction by rotating around this axis only once. Will this not cause problems? Yes, the proof method is very simple. First, take the origin of the target matrix as one angle and the three axes as three sides to establish a cube. The diagonal line passing through the origin in this cube is the rotation axis we are looking for. Obviously, this rotation axis is unique, and We know that rotating around a rotation axis at different angles corresponds to different directions (angle range (−π,π]）， It can be seen that the axis angle representation of any position in space is unique.

Generally speaking, when the axis angle represents the direction, there will be 4 parameters, 3 of which are used to represent the rotation axis and 1 is used to represent the rotation angle size. And if we specify the vector representing the rotation axis as the unit vector e, considering that $\ sqrt {x ^ 2 + y ^ 2 + z ^ 2} = 1 $, we can represent the rotation axis with two parameters, which only requires three parameters in total, as many as the Euler angle. The rotation vector can be represented by $\ bm {\ theta} =\ theta e $, where e is the unit vector. Incidentally, the rotation axis here is called the Euler axis, and the rotation vector here is called the Euler vector.

It is also possible to consider the existence of this thing from the perspective of a matrix. There is a concept of a similar matrix and an eigenvector in the matrix. You can understand that this rotation axis is the eigenvector of the Euler angle rotation matrix, and the rotation angle of this rotation axis is the eigenvector. eigenvalue.

So what is a quaternion?

A quaternion is a complex number, and more specifically a quaternion is a complex number with three imaginary parts. q = w + ix + jy + kz, where i, j, k are imaginary units, such that i ^ 2 = j ^ 2 = k ^ 2 = -1, and i (j) j = k, j (i) i = k.

q1+q2=(w1+w2)+i(x1+x2)+j(y1+y2)+k(z1+z2)=[(w1+22),(v1+v2)]q1⋅q2=(w1w2−x1x2−y1y2−z1z2)+i(w1x2+x1w2+y1z2−z1y2)+j(w1y2−x1z2+y1w2+z1x2)+k(w1z2+x1y2−yzx2+z1w2)q_1 + q_2 = (w_1 + w_2) + i(x_1 + x_2) + j(y_1 + y_2) + k(z_1 +z_2) = [(w_1 + 2_2), (v_1 +v_2)] \\ q_1 \cdot q_2 = (w_1w_2 -x_1x_2 - y_1y_2 - z_1z_2) + \\ i(w_1x_2 + x_1w_2 + y_1z_2 - z1y_2) + \\ j(w_1y_2 - x_1z_2 + y_1w_2 + z_1x_2) + \\ k(w_1z_2 + x_1y_2 -y_zx_2 + z_1w_2)

When using quaternions to compute axis angle representations, we usually write them in vector representation, $q =\ begin {bmatrix}
W,\ vec v\ end {bmatrix} =\ begin {bmatrix} w,\ begin {pmatrix} x\ y\ z\ end {pmatrix}\ end {bmatrix} $, for clarity of expression and convenience of calculation, we position the value of w, x, y, z $w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2 = 1 $, and call it the unit quaternion. In the direction calculation, the role of w, x, y, z in the unit quaternion is behind us Will explain. At this point, complex multiplication can be expressed in vector form

q1⋅q2=[w1,v⃗1]⋅[w2,v⃗2]=[w1w2−v1v2,v1×v2+w1⋅v2+w2⋅v1]q_1 \cdot q_2 = [w_1, \vec v_1] \cdot [w_2, \vec v_2] = [w_1w_2 - v_1v_2, v1 \times v_2 + w_1 \cdot v_2 + w_2 \cdot v_1]

Or we can also write it in the form of a matrix

q1q2=[w1−x1−y1−z1x1w1−z1y1y1z1w1−x1z1−y1x1w1][w2x2y2z2]q_1q_2 = \begin{bmatrix} w_1 & -x_1 & -y_1 & -z_1 \\ x_1 & w_1 & -z_1 & y_1 \\ y_1 & z_1 & w_1 & -x_1 \\ z_1 & -y_1 & x_1 & w_1 \end{bmatrix} \begin{bmatrix} w_2 \\ x_2 \\ y_2 \\ z_2 \end{bmatrix}

Observing this formula, we found that multiplying two quaternions requires storing 8 units of data, that is, each quaternion involved in the operation only needs to store 4 units of data. In addition, several special properties are required:

  • Quaternion modulo $| | q | | =\ sqrt {w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2} $
  • Quaternion conjugate $q ^{} = ( w + ix + jy + kz )^{}= w -ix -jy - kz $
  • 共轭的向量形式q∗=([wv⃗])∗=[w−v⃗]q^{*} = (\begin{bmatrix} w & \vec v \end{bmatrix})^{*} = \begin{bmatrix} w & -\vec v \end{bmatrix}
  • The reciprocal of a quaternion: $q\ cdot q ^ {-1} = q ^ {-1}\ cdot q = 1 $
  • Conjugate vs. reciprocal: $q ^ {-1} =\ frac {q ^ } {w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2} $, for the unit quaternion $q ^{} = q {-1} $
  • Quaternion operations satisfy both associative and distributive laws, but do not conform to commutative laws

Knowing the above calculation rules, we can use quaternions to calculate the direction transformation process. Remember that we said before that when calculating quaternions, we use vector form to represent them and ensure that they are unit quaternions? In fact, the vector form of quaternions can be further rewritten as polar representation, $q =\ | q\ | [cos\ theta,\ vec {n}\ cdot sin\ theta] $

Where q represents the modulus of the quaternion, the modulus of the quaternion is 1, and θ is the half-angle size of the rotation process represented by the quaternion, that is to say, (2θ) is the size of the rotation angle, and n is the rotation axis. The unit vector of direction. With this representation, the quaternion can represent the direction transformation expressed by any axis angle.

First, the original vector coordinates are expressed as quaternions $p = [0,\ vec {v}] $, and the rotation angle and rotation axis are expressed as unit quaternions q. The rotated vector coordinates can be obtained by $r = q\ cdot p\ cdot q ^ * $or $r = q\ cdot p\ cdot q ^ {-1} $

Why introduce quaternions

In fact, the quaternion is to better represent the rotation axis and rotation angle. The rotation axis is a three-dimensional vector, and the rotation angle becomes four-dimensional. The quaternion was chosen to represent it because of some of its characteristics.

Let’s start with the conclusion that quaternion references are used to reduce the amount of computation and storage space occupied during computation.

However, if you are careful enough, you can definitely find that the process of multiplying two quaternions is actually a process of multiplying a 4 × 4 matrix with a 4 × 1 matrix, and the quaternion calculation requires two times this process, including 24 addition operations and 32 multiplication operations. In contrast, the matrix transformation of the Euler angle only needs to perform a multiplication operation of a 3 × 3 matrix and a 3 × 1 matrix, including 6 addition operations and 9 multiplication operations. The amount of operation is obviously Quaternion is larger. If you are more careful, you can find that although there is a 4 × 4 matrix involved in the operation of the quaternion operation, each item in the matrix is the unit data that has been stored, and the 3 × 3 matrix involved in the Euler angle operation It is obtained by 16 multiplication operations, 4 addition operations and 4 sign change operations performed on the stored unit data, but even with these operations, the matrix operation only needs 25 multiplication operations, 10 addition operations and 4 sign change operations. In terms of computational volume, the matrix operation of Euler angles still has an advantage over the quaternion operation. But in fact, the kinematics problems we generally encounter rarely have to do only one direction conversion. For complex systems and robots, we often face a large number of direction conversion processes. In this case, the advantages of quaternions are reflected. We consider quaternion operations for multiple transformations (using the polar coordinate form above):

R=R1R2...Rn−1Rn=(qn(qn−1...(q2(q1pq1∗)q2∗)...qn−1∗)qn∗)R = R_1R_2...R_{n-1}R_n = (q_n(q_{n-1}...(q_2(q_1pq^*_1)q^*_2)...q^*_{n-1})q^*_n)

Use associative law:

R=R1R2...Rn−1Rn=(qnqn−1...q2q1)p(q1∗q2∗...qn−1∗qn∗）R = R_1R_2...R_{n-1}R_n = (q_nq_{n-1}...q_2q_1)p(q^*_1q^*_2...q^*_{n-1}q^*_n）

Consider the conjugate $ (q_aq_b) ^ *= q ^ * _bq ^ * _a $

R=R1R2...Rn−1Rn=(qnqn−1...q2q1)p(qnqn−1...q2q1)∗R = R_1R_2...R_{n-1}R_n = (q_nq_{n-1}...q_2q_1)p(q_nq_{n-1}...q_2q_1)^*

It can be found that the operation result in the parentheses on the left and right sides of the original vector ppp is a pair of conjugated quaternions, that is to say, the 3-th easy sign operation can be used instead of the n-th quaternion multiplication operation, which greatly reduces the amount of calculation.

Finally, a little mention, a lot of people who come into contact with this problem are game developers, may have doubts, why there is no such problem in Unity’s Inspector, you can try this, Unity’s Inspector in the Y axis is not the object’s own coordinate axis rotation, so the universal lock is solved, the specific Unity internal rotation is how to see the next blog, here to dig a pit

Reference article:

欧拉角 - 维基百科

如何通俗地解释欧拉角？之后为何要引入四元数？