GAMES101 Series Summary (3) - Shading

Currently, we have introduced the following steps in graphics:

• The first three figures show the MVP matrix converting the coordinates of each point on the model into screen space
• The last figure shows the process of grating the triangular panels that connect the points in the converted screen space, that is, to determine which pixels each triangular panel will affect

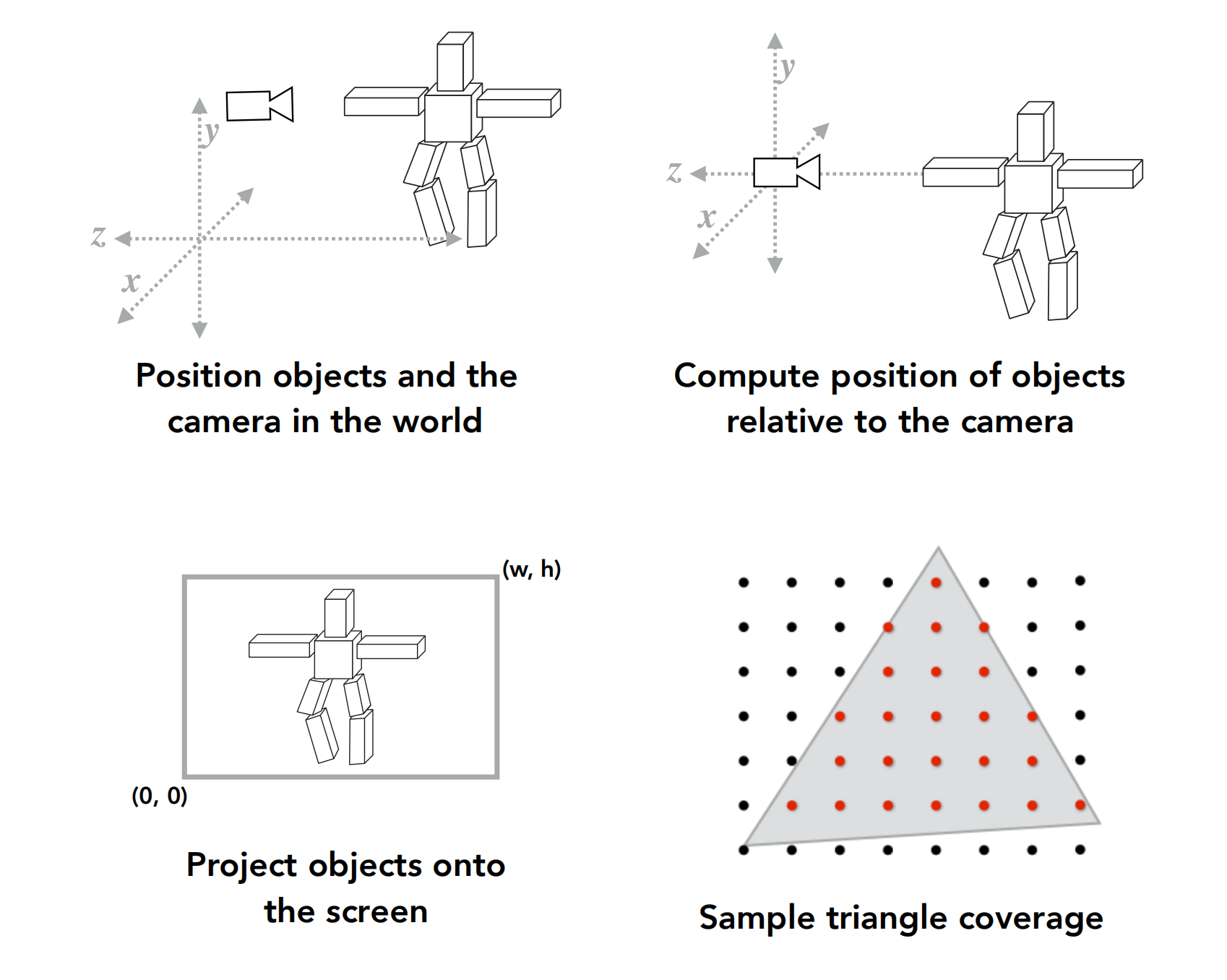
But so far, we’ve only got the coordinates of each point in screen space and which pixels it affects, but what the specific impact is, we haven’t got it yet.

The next process we talk about shading is how to calculate the impact of these points on pixels.

The English translation of shading is: The darkening or coloring of an illustration or diagram with parallel lines or a block of color, which is what we usually call shadow

But in Computer Graphics, it refers to the process of calculating the effect of these points on pixels, that is, the color of these points.

Here we think about a question, how do we see objects in everyday life: the optical part of physics We all know this problem, ** the reason why we can see an object is because the light reflected by the object enters our eyes **, the color and angle of the reflected light will affect our observation of the object

So we also use this theory in graphics, and our shading process is to calculate the angle and color of the reflected light at each point.

So how can we use this theory to calculate the process of physical illumination?

First, we need to model the illumination model, that is, what the result of the illumination of an object is composed of.

This modeling is also divided into several parts:

• A point can be affected by several different lights
• What kind of calculation method does each different illumination follow, such as the color, angle, intensity, etc. of each illumination?
• How different lighting effects stack up at a certain point
• We get the lighting effect of different points, how to calculate the effect of each pixel in the triangle, is the color of each pixel in the direct triangle is just three points, simply average or what?
• Finally, what is the input for each point calculation? Such as the color of each point, what is the normal vector, etc

Here we use a relatively simple Bollinger-von model to introduce, other models may be more complex than this, but only the specific algorithm may be different, but the steps are still these steps

There are several different kinds of light at one point

In this model, we divide the reflected light of an object into three parts:

• Specular highlight: reflected light with a relatively fixed exit angle
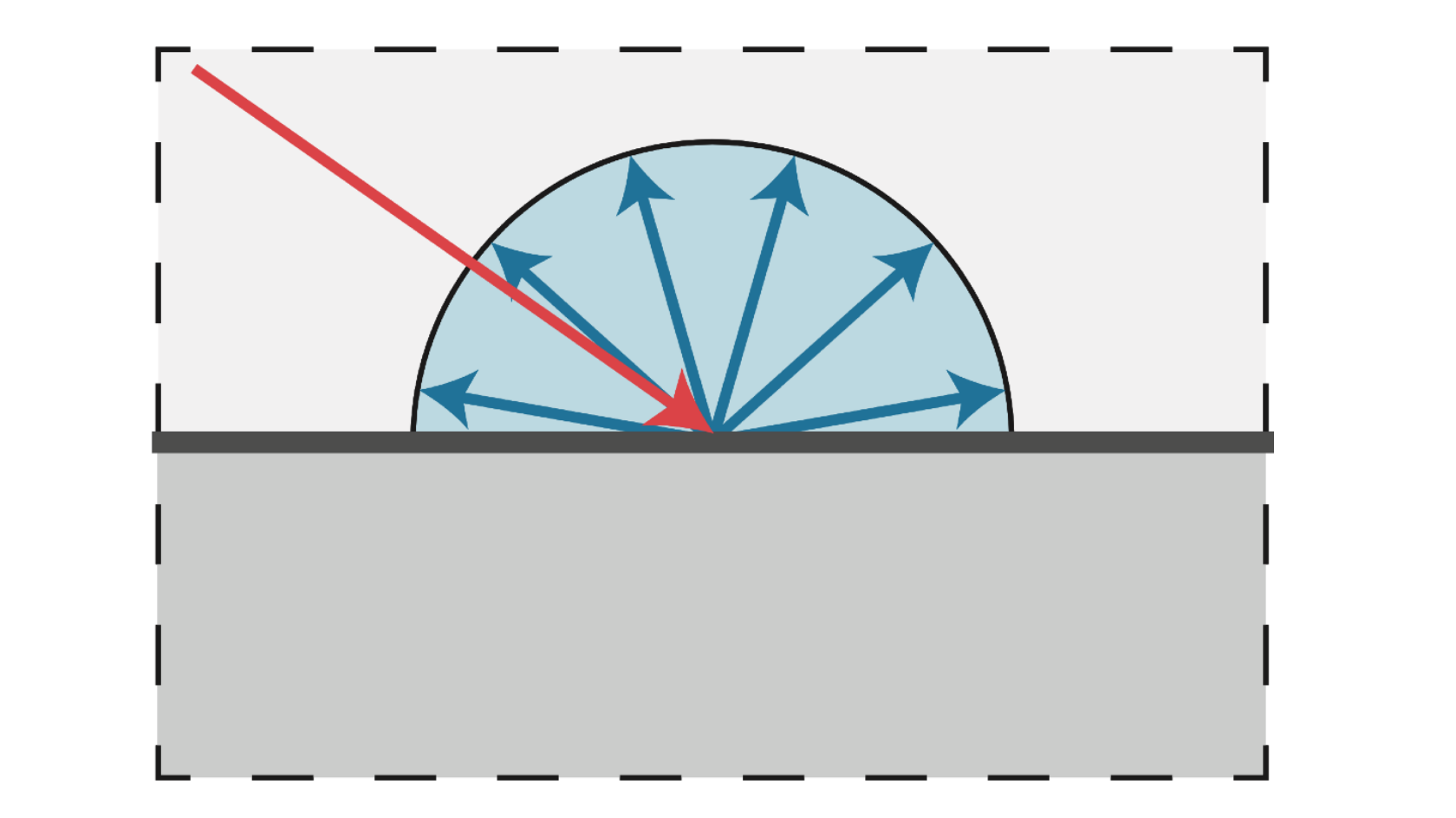
  Diffuse reflection: Light reflected in all directions
• Ambient lighting: that is, assuming there is no light source in the environment, nor is it black, there is always a little light

Note that if you have used Unity in the past, you may be exposed to several concepts, such as direct light and indirect light. This concept has nothing to do with specular reflection and diffuse reflection here. At the same time, there is also a concept in Unity called self-luminous, which is not the same as ambient light.

How to calculate the lighting effect on a point

So how do we calculate the lighting effect at a point on the model?

The first is what inputs we have when calculating the lighting effect of a point:

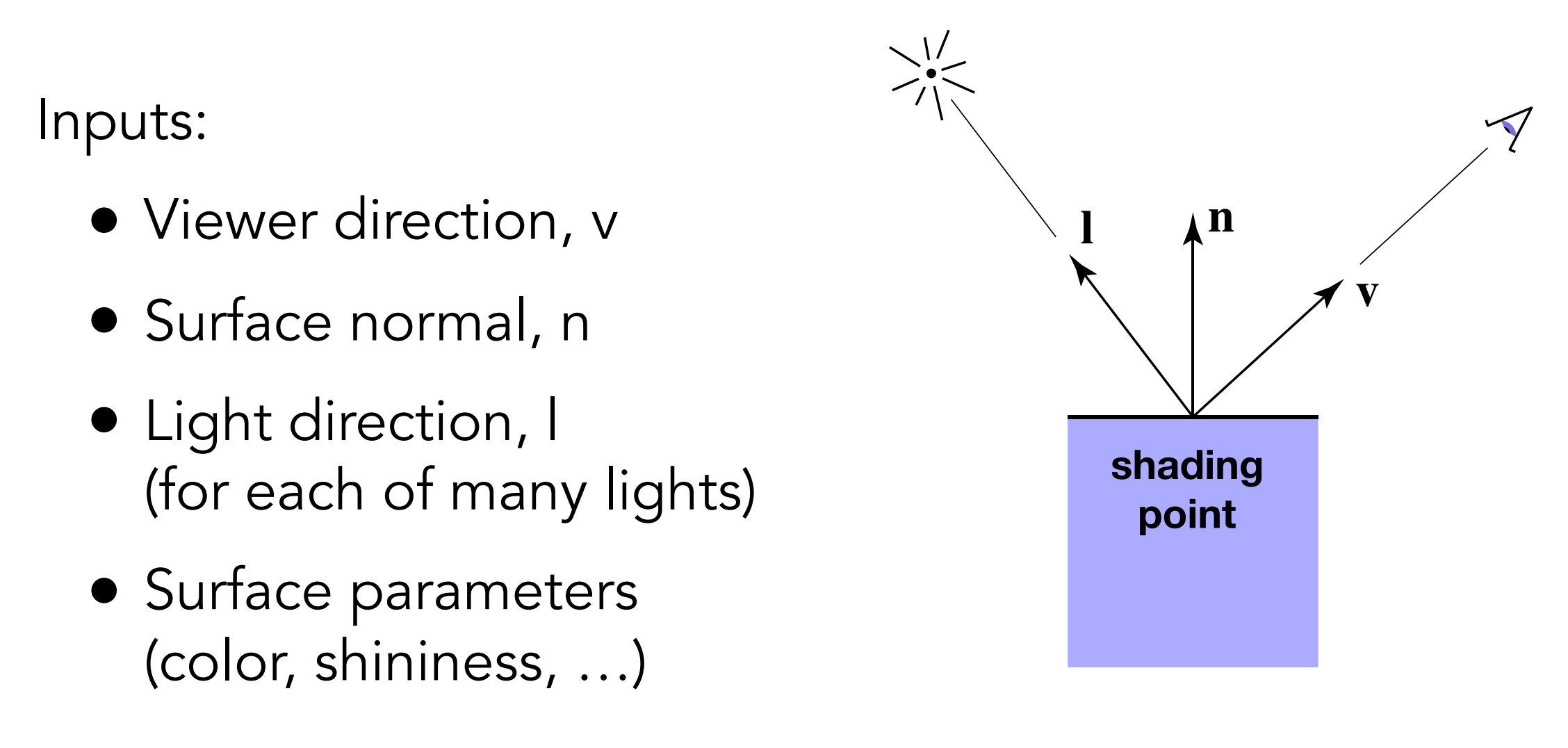
** Note that the v vector above is not the direction of the outgoing light, but the direction of the line between the reflection point and the camera **

So with these inputs, how do we calculate the lighting effect of a certain light at this point?

Diffuse illumination

The so-called diffuse reflection is the light reflected at all angles, and the reflection angle we get

So what about the intensity of the reflected light? That is, how is the light and shade of this point determined?

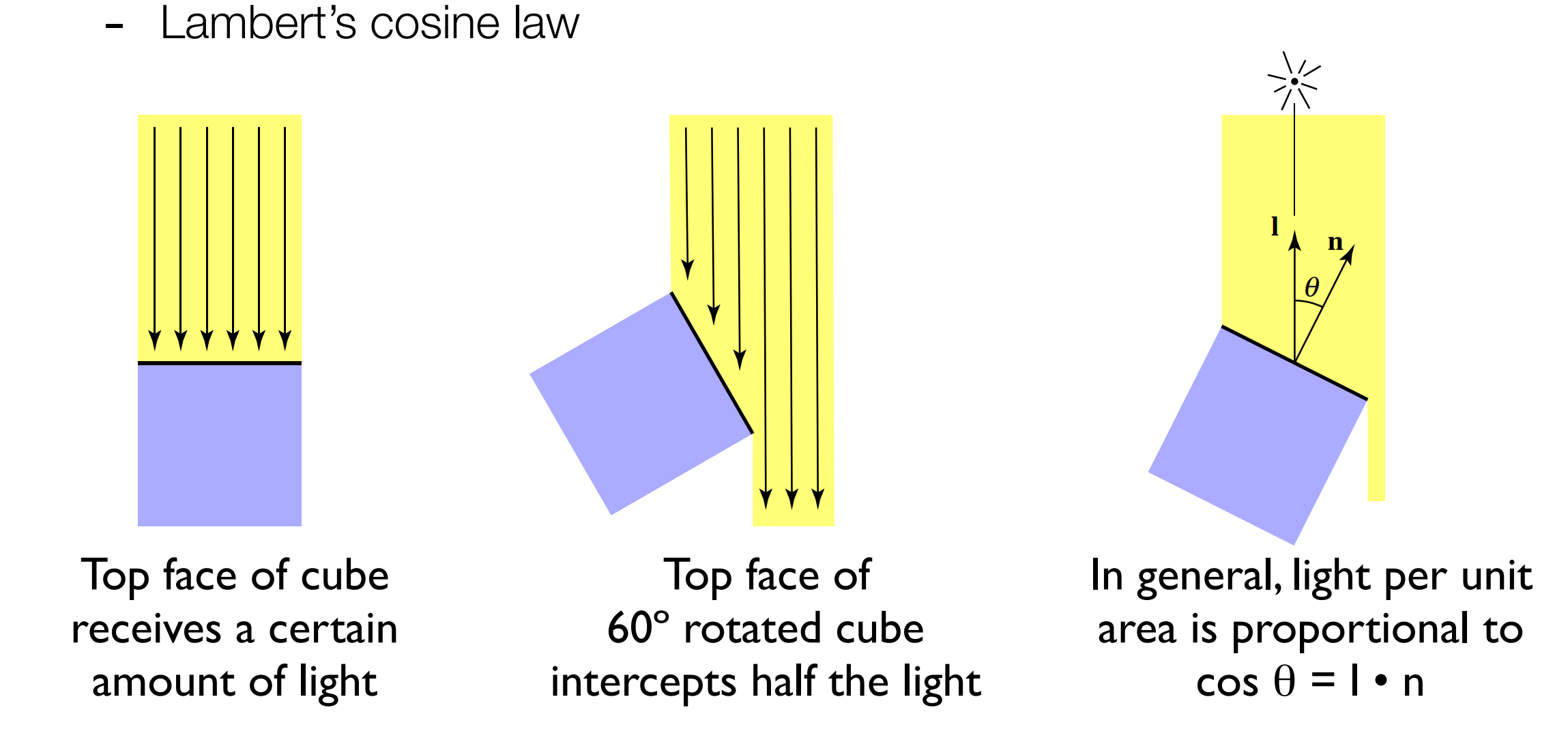
The model we take assumes that the illumination is a collection of light of uniform density. When your plane is not perpendicular to the light, there will be a part of the light that is not reflected. We pass the direction between the normal direction and the direction of the incident ray. The angle cosine calculates how much intensity the reflected light loses at the reflection point.

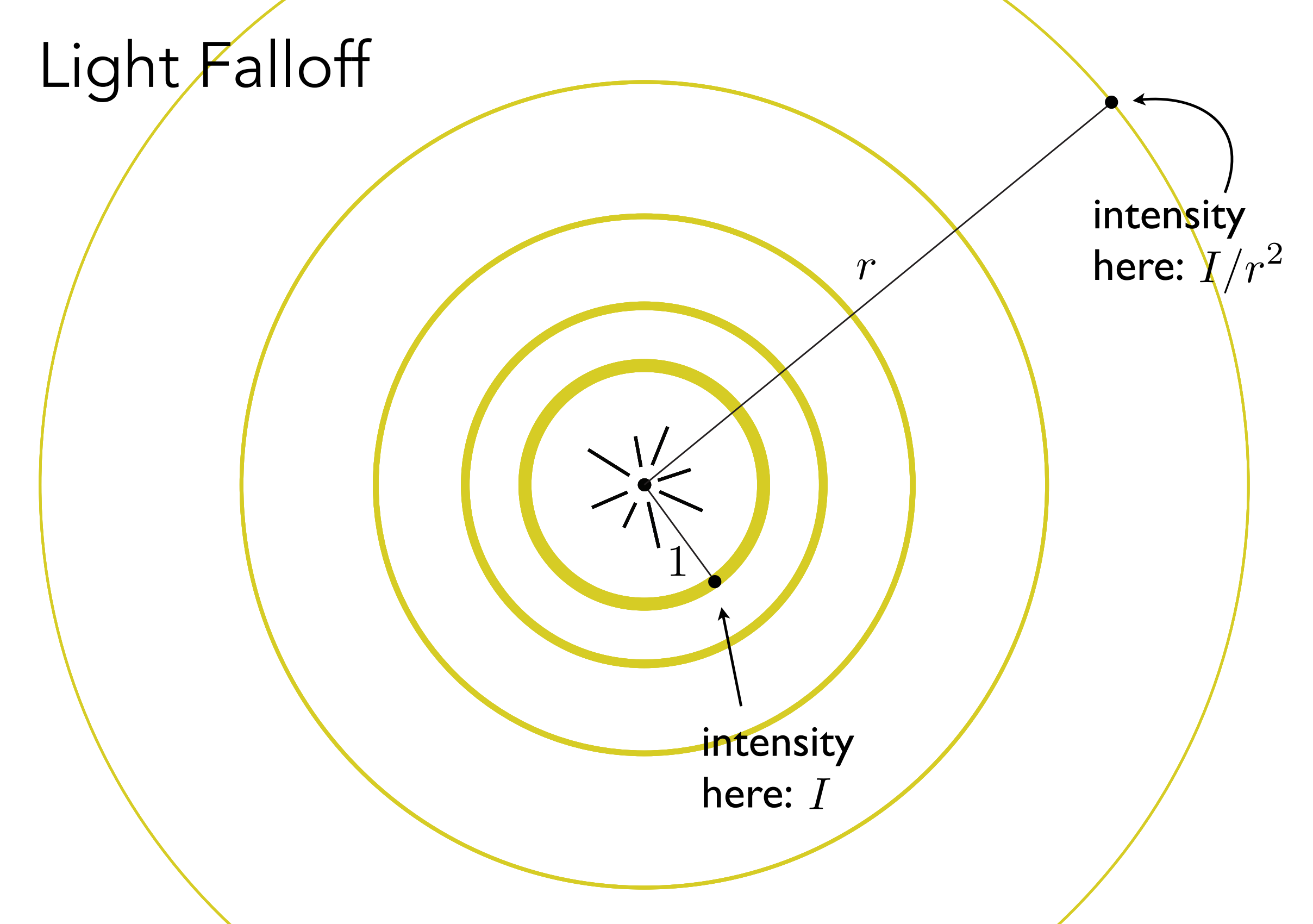
Another problem is that as the distance increases, the energy of the light will gradually decay. We also simply use the following model to calculate the energy decay during the propagation process

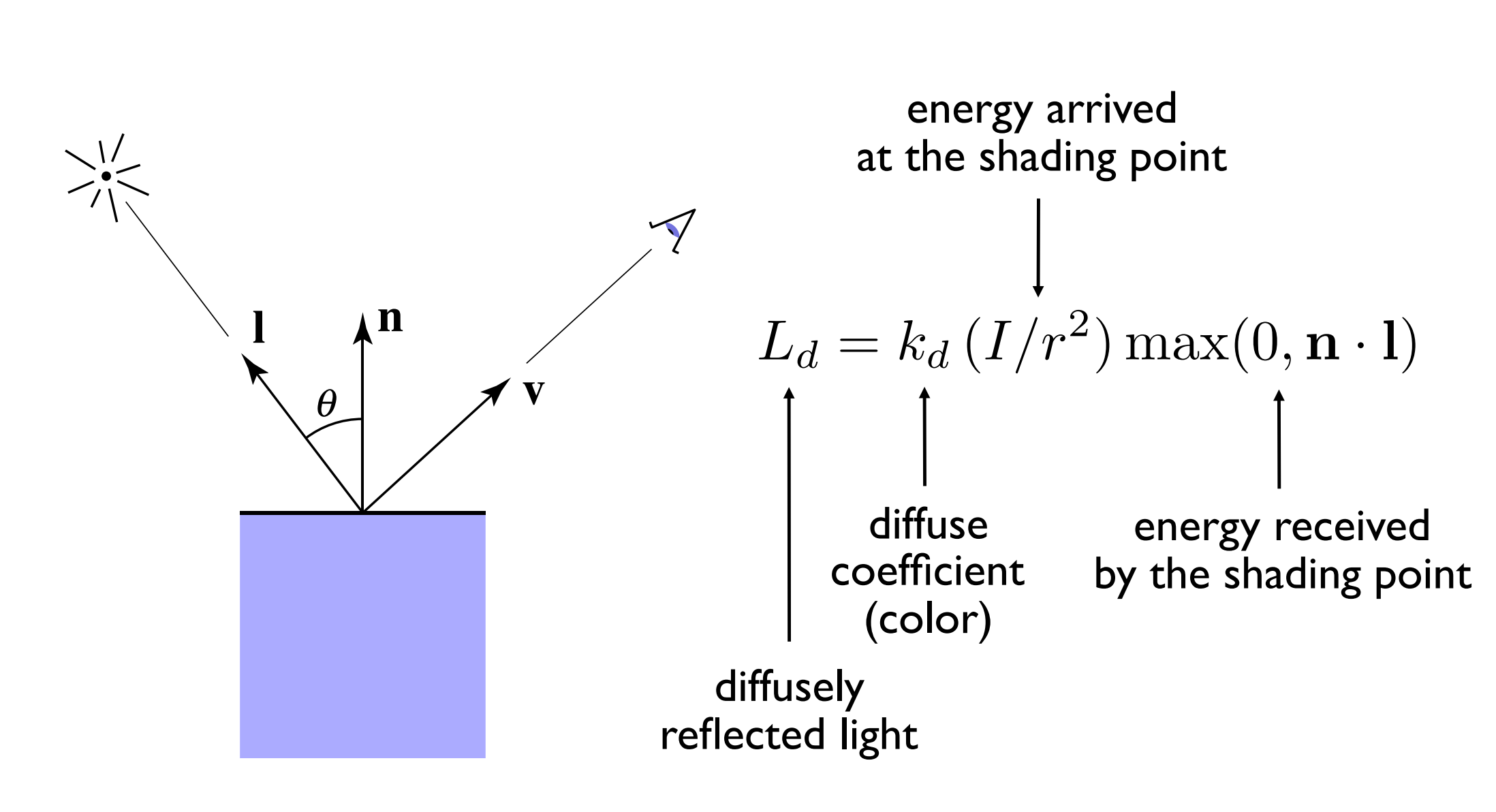
Adding this dot color value, we get this dot lighting effect (we will talk about how this color comes from later)

** The $K_d $in the formula below is the diffuse reflection coefficient, which can be more than the color of this point **

Note that the real physical lighting model is much more complicated than this, but simulating the real physical lighting is theoretically impossible. There is a model that can perfectly restore the physical world, and secondly, even if it is possible, the amount of calculation is too large.

Highlight reflection

For specular reflection, the direction of the incident ray and the direction of the outgoing light are symmetrical about the normal, while the direction of the outgoing light and the observation direction are about close, and the fresh fruit of the high light reflection is more obvious

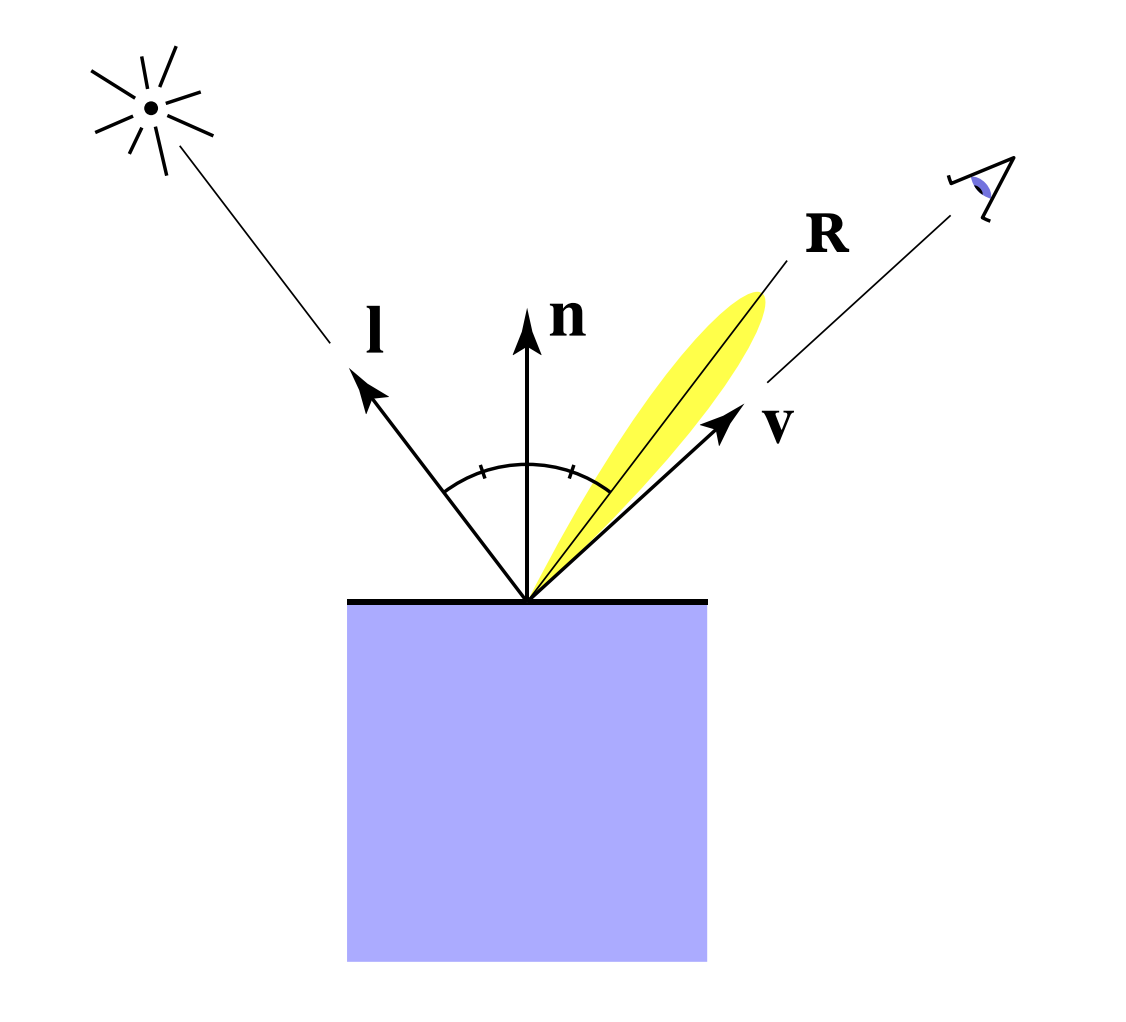
That is to say, R and V are about close, and the highlight is more obvious

However, the Blinn-Phong model uses something called a half-pass vector to calculate the proximity of R and V, as shown in the following figure:

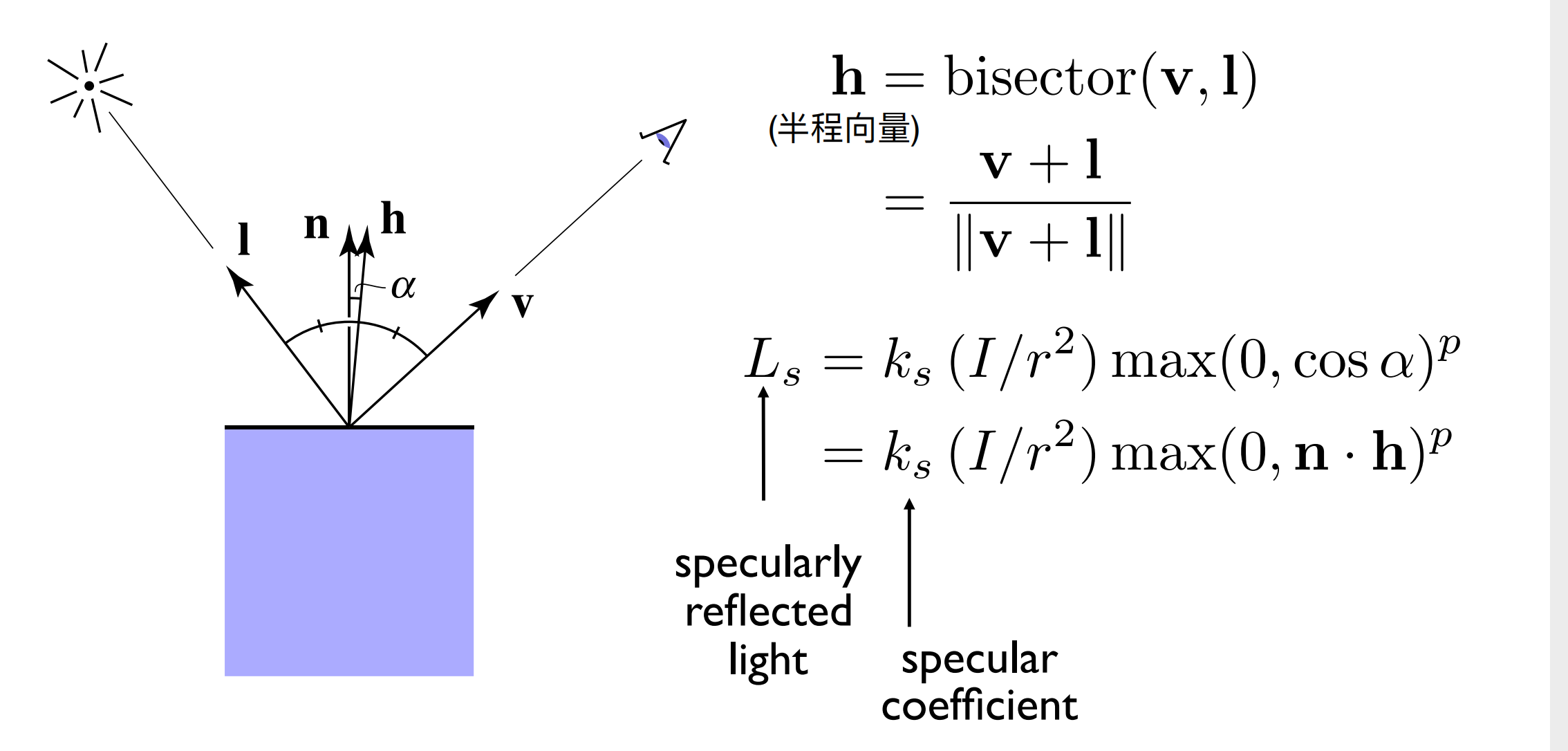
The $K_s $in this formula is the highlight coefficient, which can be the color of this point

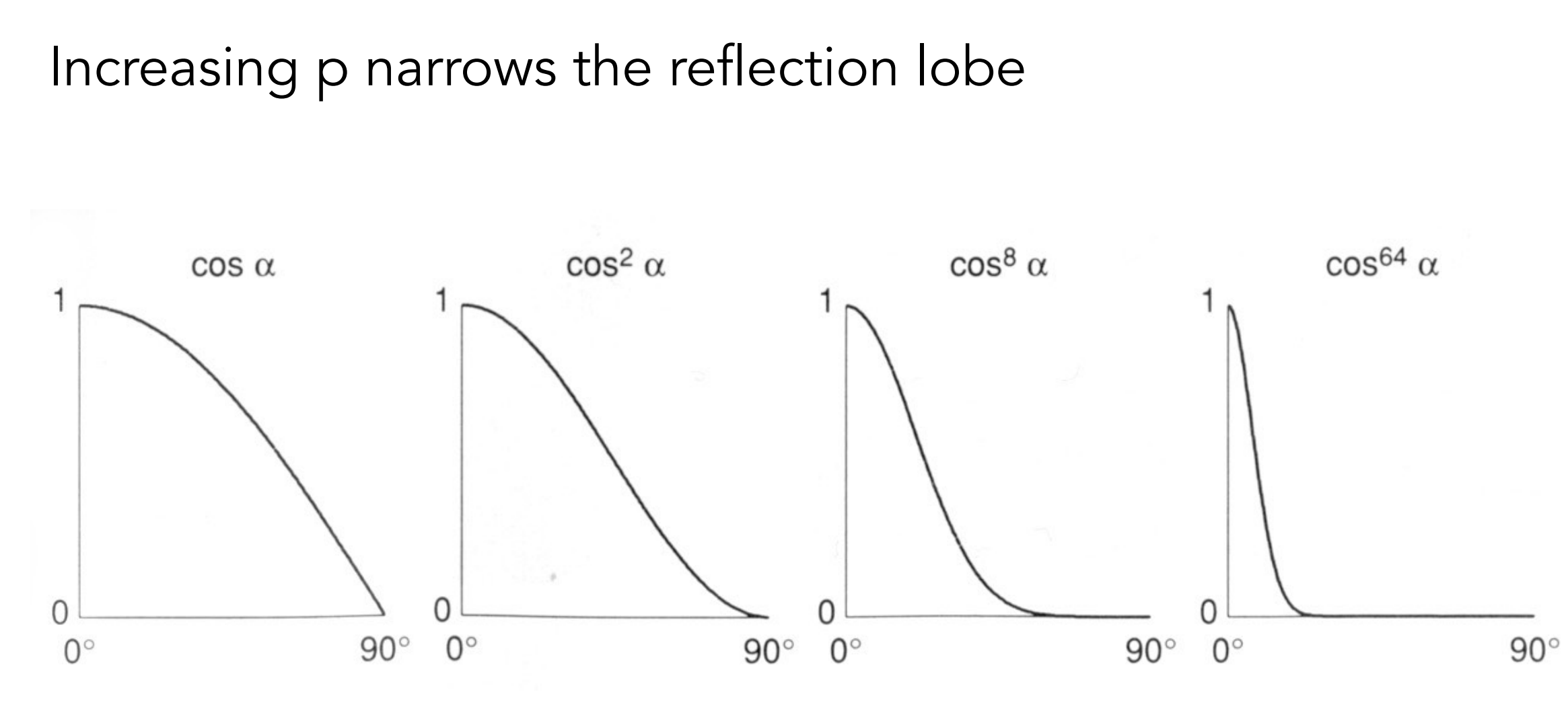
We notice that in this formula, there is a p, and this p will eventually affect the range of highlights:

Ambient light

Ambient light We simply assume that each point has a fixed light, and similarly, the ambient light coefficient can be just the color of this point

How to superimpose different light effects on one point

For the Blinn-Phong model, it’s very simple, just add

How to get the lighting effect of a triangular surface based on three points

We also have several different ways to calculate the effect of different pixels on a surface:

• ** Flat ** Shading: The first is simpler, the normal vector of all points on this surface is the same, which can be directly calculated from the coordinates of three points
• ** Gouraud ** shading: interpolate using the colors of three points, each with its own normal vector
• ** Phong ** Shading: It is also interpolated, but Phong shading calculates the color value at each pixel, not at the vertex

Gouraud

Through this interpolation process, we can obtain a smooth color gradient effect, making the color change of the triangle surface more natural.

Gouraud

Phong

The picture below shows the effect in three different ways as the number of faces increases.

There are also different ways to get the normal vector of each point. For example, for a sphere, the normal direction is the direction of the connection between the center of the sphere and a point on the surface of the sphere. For ordinary geometry, we can calculate on several different surfaces of a point, calculate the normal vector of each surface separately, and then average it. There are many ways, just choose the right one.

Texture

So far we have talked about MVP matrices, triangulation, grating, lighting calculations, etc. We still need the last link, that is, we have talked about the calculation process before, and we have not talked about the input source of this process.

But before we get to that, let’s string together our previous knowledge and look at when we get and use these inputs.

The content that connects these knowledge is called rendering pipeline. In fact, I have talked about it in my previous blog, so I will not go into detail here. You can read my previous blogUnity渲染流水线（一）从模型上的点到屏幕上的点：

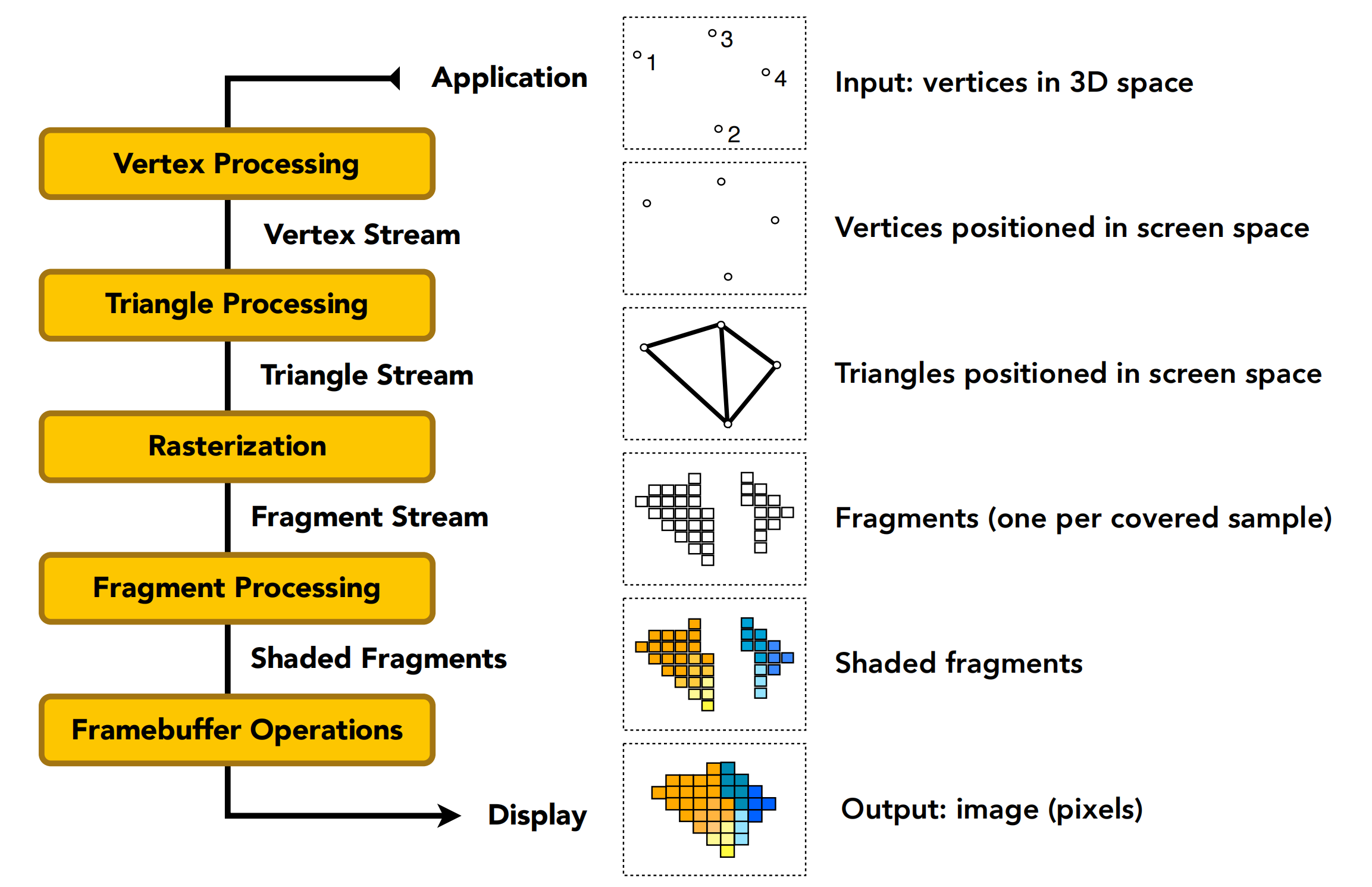
In this rendering pipeline, we can customize the programming, the first step and the fourth step, respectively, corresponding to the vertex shader and the slice shader. Like triangulation and rasterization, although we spent some time to understand its principle, what problems will be encountered, how to optimize, but in fact this process is Hardcode in the GPU.

In this calculation process, the final point will become a different color, which is determined by the input. We can set our own properties for each point, including the color of the point, the normal direction, etc., and the input method is Through Texture, that is, stickers can not only be used to control the color of each point, but also the properties of any point.

The specific application method is that each point of the model can have several sets of UV coordinates in addition to its own position coordinates. This is a two-dimensional coordinate, indicating the property corresponding to the coordinates of a certain property of this point on the map. For example, the UV coordinates of the color of a point are (0.5, 0.5), so the color of this point is the color of the corresponding point on the map (0.5, 0.5).

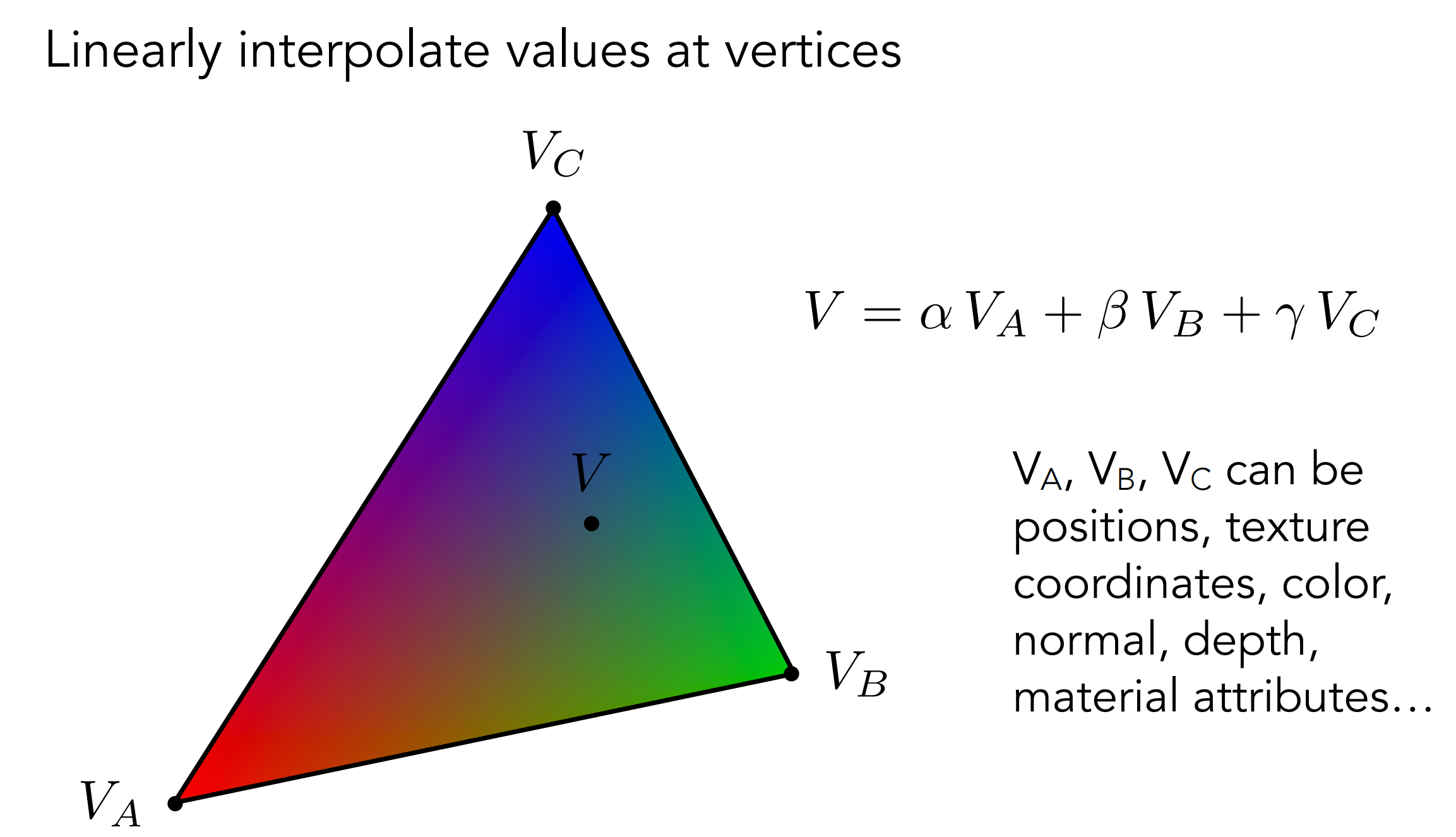
But now the problem is that we can only set properties for a certain point. For a triangular patch, how do we calculate the property value of one of the points? Let’s illustrate it with Gouraud Shading, which involves something called barycentric coordinates.

The so-called barycentric coordinate is a set of coordinates inside the triangle. For a certain triangle, any point inside it can be represented by this coordinate system

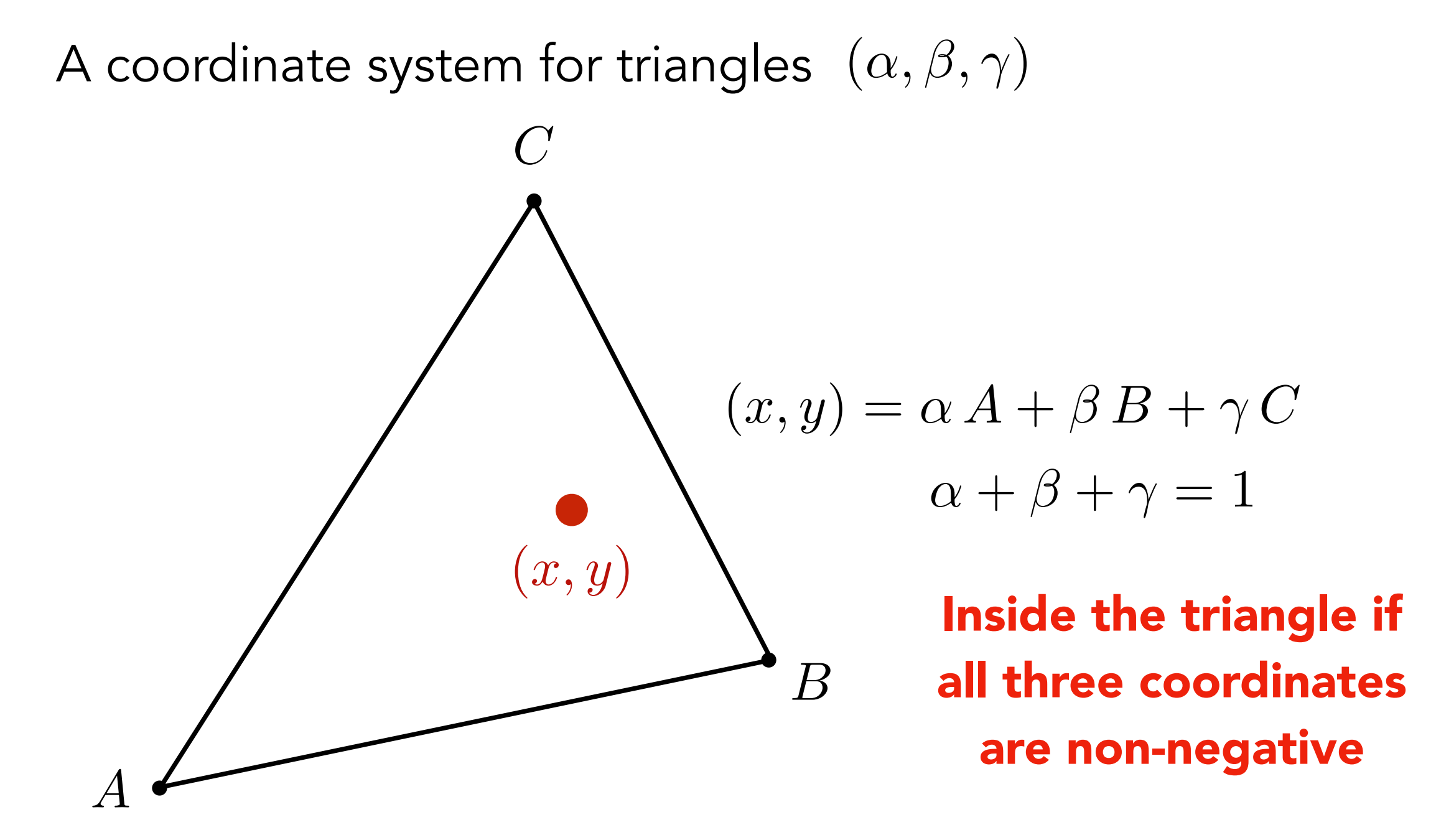
So what is the use of this coordinate system? As follows:

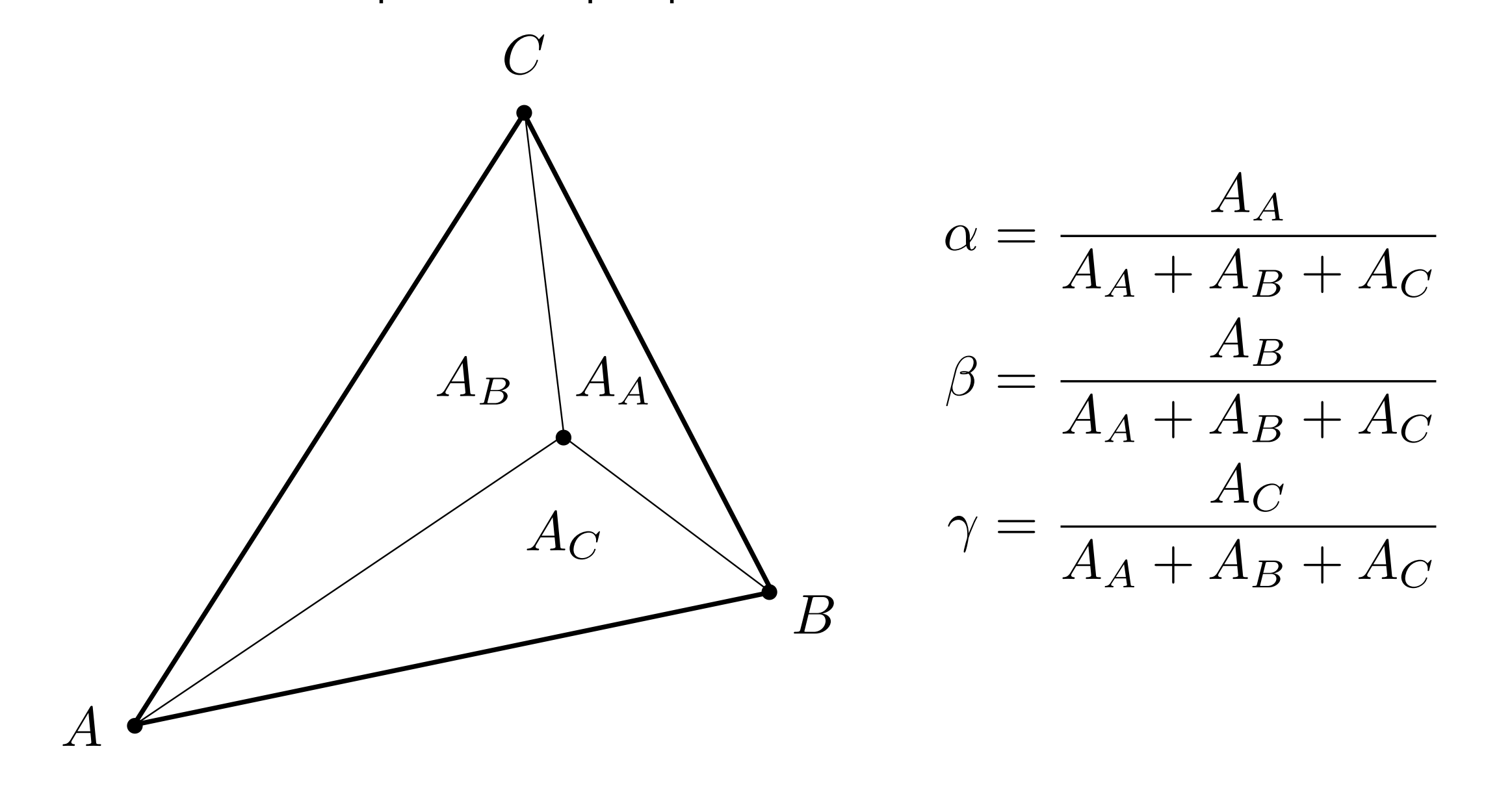
It can represent the area ratio of the three triangles divided into the interior, so that we can use barycentric coordinates to calculate the influence of the three vertices on the current point in the interpolation process of any point: