Backtracking Algorithm

Principle

Recently, I encountered several backtracking algorithms when I was doing problems, and each time I tried them out slowly, so I went to find out if there was any abstract ideas that I could refer to, so I looked for many articles, and here is an excerpt of the most basic but also the most clear article, the original link is this permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/).

Solving a backtracking problem is actually a decision tree traversal process. You only need to think about 3 questions:

1. Path: that is, the choices that have been made.

2. The list of choices: that is, the choices you can currently make.

3, the end condition: that is, the condition that you can no longer make a choice when you reach the bottom of the decision tree.

If you don’t understand the explanation of these three terms, it’s okay, we will use the classic backtracking algorithm problems of “Full Alignment” and “N Queen Problem” later to help you understand what these terms mean, for now you stay impressed.

In terms of code, the framework of the backtracking algorithm:

result = []
def backtrack(path, list of choices).
    if end condition is met.
        result.add(path)
        return
    for selection in selection list.
        Make a selection
        backtrack(path, selection list)
        Undo selection

The core of this is the recursion inside the for loop, “do selection” before the recursive call, and “undo selection” after the recursive call, it is very simple.

What do you mean by “choose” and “undo”, and what is the underlying principle of this framework? Here we will unravel the previous doubts through the problem of “full alignment” and explore the mystery in detail!

Example

Full alignment problem

We have done math problems with permutations in high school, and we know that there are n non-repeating numbers, and there are n!

PS: For the sake of simplicity and clarity, we are discussing the full permutation problem without repeating numbers.

So how did we exhaust the full permutations then? Let’s say you are given three numbers [1,2,3], you will not exhaust them in a random way, but generally as follows:

First fixed the first for 1, then the second can be 2, then the third can only be 3; then you can turn the second into 3, the third can only be 2; then you can only change the first, into 2, and then exhaust the last two …

In fact, this is the backtracking algorithm, we will use it in high school without any teacher, or some students directly draw this backtracking tree as follows:

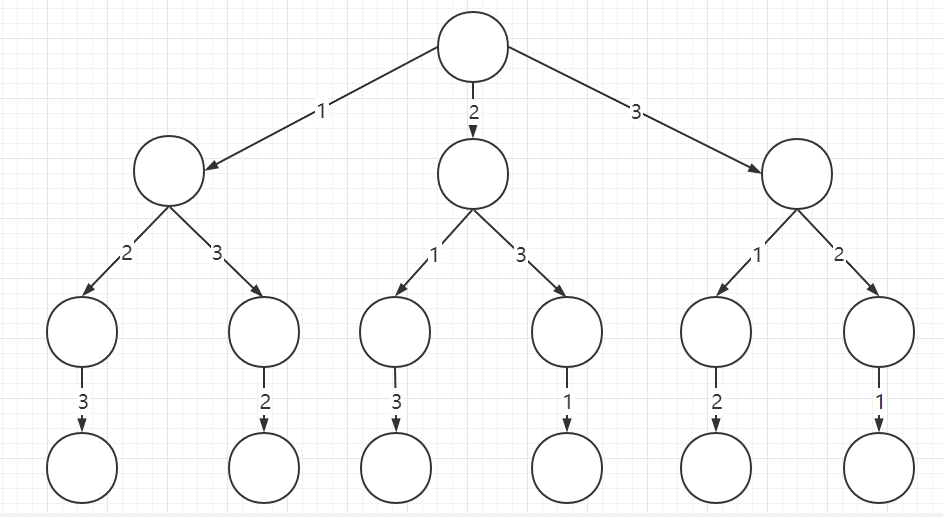
Just traverse this tree from the root and record the numbers on the path, which are actually all the full permutations. We might call this tree the “decision tree” of the backtracking algorithm.

Why do you call this a decision tree? Because you are actually making decisions at each node. Let’s say you are standing on the red node in the following figure:

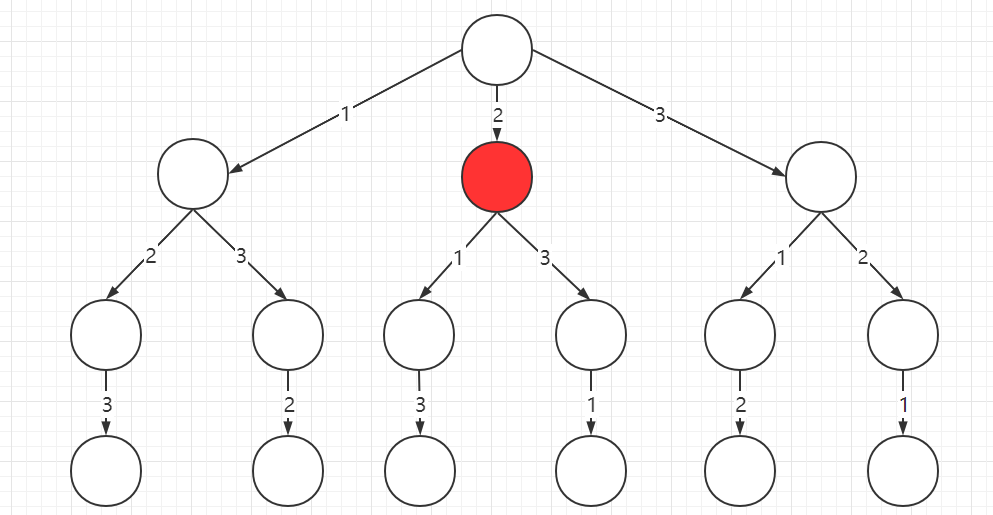
You’re making a decision right now. You can choose either the 1 branch or the 3 branch. Why can you only choose between 1 and 3? Because the 2 branch is behind you, you’ve done this before, and full alignment doesn’t allow reuse of numbers.

Now we can answer the first few terms: [2] is the “path”, which records the choices you have already made; [1,3] is the “choice list”, which indicates the choices you can currently make; “end condition” is the traversal to the bottom of the tree, in this case when the choice list is empty.

If you understand these terms, you can use the “path” and “choice” lists as attributes of each node in the decision tree, for example, the following figure lists the attributes of several nodes:

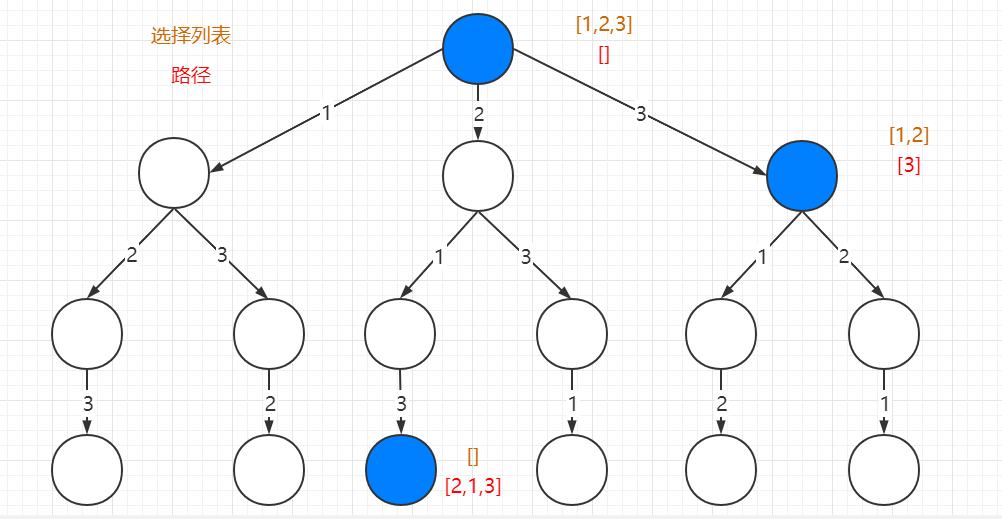
The backtrack function we defined is actually like a pointer that wanders around the tree while maintaining the properties of each node correctly, and whenever it goes to the bottom of the tree, its “path” is a full alignment.

Further, how to traverse a tree? This should not be difficult. Recall that the previous “framework for learning data structure thinking” wrote that various search problems are actually tree traversal problems, and the traversal framework of multinomial trees is as follows:

void traverse(TreeNode root) {
for (TreeNode child : root.child)
// The operations needed for a preorder traversal
traverse(child).
// operation needed for post-order traversal
}
And the so-called preorder traversal and postorder traversal, they are just two very useful points in time

Pre-order traversal code is executed at the point in time before entering a node, and post-order traversal code is executed at the point in time after leaving a node.

To recall what we just said, “path” and “selection” are properties of each node, and for the function to properly maintain the properties of the node as it wanders through the tree, it has to do something at these two special times:

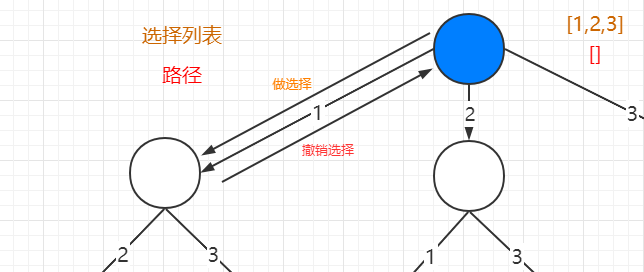
Now, do you understand this core framework of the backtracking algorithm?

for select in Select list.
    # Make a choice
    Remove the selection from the selection list
    path.add(selection)
    backtrack(path, selection list)
    # Undo the selection
    path.remove(selection)
    Add the selection to the selection list again

We just need to make the selection before the recursion and undo the selection we just made after the recursion to get the correct list of selections and paths for each node.

Own implementation of the JavaScript code:

/**
 * @param {number[]} nums
 * @return {number[][]}
 */

const swap = (nums, i, j) => {
    let temp = nums[i].
    nums[i] = nums[j].
    nums[j] = temp.
}

const generate = (nums, output, n, first) => {
    if (first === n) {
        output.push([. .nums]).
    }
    for (let i = first; i < n; i++) {
        swap(nums, i, first).
        generate(nums, output, n, first + 1).
        swap(nums, i, first).
    }
}.

const permute = function(nums) {
    let output = [].
    generate(nums, output, nums.length, 0).
    return output.
}.

Notes:

The pictures in this article are from labuladong public