Unity Rendering Principle (3) Rendering Pipeline - From Point on Model to Point on Screen (Matrix Edition)

I have summarized the introduction of a version of the Unity rendering pipeline before. This time, it will be clearer to reorganize the process from the perspective of the spatial transformation of the matrix. It is also a practice for me to review the content of linear algebra during this time.

The Geometric Meaning of Matrix: Transformation

The geometric meaning of the matrix is not just transformation, but the matrix also has its algebraic meaning, but for the game, it is mainly transformation. If you are interested in other meanings, you can see my other blog:

What is transformation?

Transformation refers to the process of transforming some of our data, such as points, directional vectors, or even colors, in some way.

Let’s first look at a very common type of transformation - linear transformation. Linear transformations refer to transformations that preserve vector addition and scalar multiplication, expressed in mathematical formulas:

$$f(x) + f(y) = f(x + y),\\ kf(x) = f(kx)$$

Scaling is a linear transformation, such as f (x) = 2 ** x **, which can represent a uniform scaling of size 2, that is, the modulus of the transformed vector ** x ** will be magnified twice.

It can be found that f (** x **) = 2 ** x ** satisfies the above two conditions.

Similarly, rotation is a linear transformation. For linear transformation, if we want to transform a three-dimensional vector, we need a third-order matrix to represent the transformation

Because for a three-dimensional vector, scaling is three coordinates changing the same size at the same time, and rotation is a different transformation, so three equations are needed to become a matrix, which is a matrix of order n

Linear transformation includes rotation and scaling, but also cross-cutting, mirroring, orthogonal projection, etc.

But there is a very basic transformation that is not linear, that is, translation. We consider a translation equation, f (** x **) = ** x ** + (1,2,3), this transformation is not a linear transformation, it does not satisfy vector addition. For example, we let ** x ** = (1,1,1).

$$f(x) + f(x) = (4, 6, 8),\\ f(x + x) = (3, 4, 5)$$

It can be seen that the results of the two operations are different, so we cannot use a third-order matrix to represent the translation of three-dimensional coordinates.

Therefore, we propose an affine transformation, which is a linear transformation plus a translational transformation. The method is to raise one dimension and use a fourth-order matrix to represent it

There are two questions here: first, why pursue linear transformation, second, why raise a dimension, transform and then reduce the dimension, you can translate into linear transformation

First answer the first question, from a geometric point of view, linear transformation is to transform the image to another coordinate system, and the pattern will not change before and after the transformation

As for why raising a dimension can smooth out this effect, you can take a look: https://www.zhihu.com/question/20666664

Homogeneous coordinates

When we transform the three-dimensional transformation matrix into four dimensions, we also need to convert the original three-dimensional vector into a four-dimensional vector, which is what we call homogeneous coordinates.

So how do you turn a 3D vector into homogeneous coordinates? For a point, going from 3D coordinates to homogeneous coordinates is by setting its w component to 1, and for a directional vector, its w component needs to be set to 0.

In this way, when transforming a point with a fourth-order matrix, both translational rotation and scaling will be applied to the point. However, for a vector, the effect of translation will be ignored

Decomposition base transformation matrix

When we use affine transformation for coordinate transformation, we use a fourth-order matrix. We can disassemble this matrix and divide it into four parts

$$\begin{bmatrix} M_{3 * 3} & t_{3 * 1} \\ 0_{1 * 3} & 1 \end{bmatrix}$$

The upper-left third-order matrix represents rotation and scaling, and the upper-right matrix represents translation.

Next, let’s see how to use this matrix for rotation, scaling, and translation.

Translation matrix

Let’s take a look. We perform a translation operation on a point

$$\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ z + t_z \\1 \end{bmatrix}$$

As you can see, we succeeded in turning the point (x, y, z) into (x + tx, y + ty, z + tz).

Let’s take a look at transforming a vector.

$$\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 0 \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\0 \end{bmatrix}$$

Translation has no effect on the vector

The Inverse Matrix of the translation matrix is obtained by reverse translation, that is:

$$\begin{bmatrix} 1 & 0 & 0 & -t_x \\ 0 & 1 & 0 & -t_y \\ 0 & 0 & 1 & -t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

It can be seen that the translation matrix is not an orthogonal matrix

Scaling matrix

We can scale the coordinates of a point, represented by a matrix:

$$\begin{bmatrix} k_x & 0 & 0 & 0 \\ 0 & k_y & 0 & 0 \\ 0 & 0 & k_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} k_xx \\ k_yy \\ k_zz \\1 \end{bmatrix}$$

Scaling a vector

$$\begin{bmatrix} k_x & 0 & 0 & 0 \\ 0 & k_y & 0 & 0 \\ 0 & 0 & k_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 0 \end{bmatrix} = \begin{bmatrix} k_xx \\ k_yy \\ k_zz \\0 \end{bmatrix}$$

The matrix above is only suitable for scaling along the coordinate axis. If we want to scale in any direction, we need to use a composite transformation. One of the main ideas is: first transform the scaling axis into a standard coordinate axis, then apply the standard scaling seen above, and then use your transformation to get the original scaling axis direction.

This process actually implies the content of a similar matrix. The above composite transformation is of the form P ^ {-1} AP, if P ^ {-1} AP

Rotation matrix

Rotation is the most complex of the three matrices. We know that the rotation operation requires specifying an axis of rotation, which is not necessarily a coordinate axis, but we will talk about rotating along the coordinate axis for now.

The matrix rotated around the x-axis is:

$$R_x(θ) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cosθ & -sinθ & 0 \\ 0 & sinθ & cosθ & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Rotate around y-axis

$$R_y(θ) = \begin{bmatrix} cosθ & 0 & sinθ & 0 \\ 0 & 1 & 0 & 0 \\ -sinθ & 0 & cosθ & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Rotate around the z-axis:

$$R_z(θ) = \begin{bmatrix} cosθ & -sinθ & 0 & 0 \\ sinθ & cosθ & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Composite transformation

We can combine translation, rotation, and scaling to form a complex transformation.

We use a column matrix to represent a point, scaling, rotating, and translating in turn (this order cannot be changed), which is expressed as:

$$p_{new} = M_{translation}M_{rotation}M_{scale}p_{old}$$

The reason why this order cannot be changed is because only in this order can we get the result we want. If we translate first and then scale, it may lead to deformation

Coordinate space

Our previous article said that the function of the vertex shader is to convert the vertex coordinates on the model to homogeneous coordinates. The process of game rendering is actually the process of converting points on the model into points on the screen through layers.

Transformation matrix of coordinate space

To define a coordinate space, we must specify its origin and the positions of its three coordinate axes.

And these, in fact, are relative to another coordinate system, that is to say, all coordinate spaces are relative, and each coordinate space is a subspace of another coordinate space.

Assuming that we now have a parent coordinate space P and a child coordinate space C, we know that in the P coordinate space, the origin of C and the directions of the three coordinate axes, we generally have two requirements, one is to change the C coordinate space The point Ac becomes Ap in the P coordinate space, and the second is the other way around.

We can represent this process with two matrix transformations:

$$A_p = M_{c->p}A_c\\ A_c = M_{p->c}A_p$$

The above two matrices represent the transformation from C to P and the transformation from P to C, which are Inverse Matrices, so how should we solve for these two matrices?

We can understand from a geometric point of view that the coordinates of a point are (a, b, c), which means that the point has moved a, b, c three units along the x, y, and z axes from the origin.

In the same way, if Ac is (a, b, c), then from the origin Oc of C, three units a, b, c have been moved along the x, y, and z axes, respectively.

So if you look at it from the perspective of P, this point first moves from the origin Op of P to Oc, and then moves from Oc to Ac.

This process is expressed in a formula:

$$\mathbf A_p = \mathbf O_c + a\mathbf x_c + b\mathbf y_c + c\mathbf z_c$$

And our transformation matrix is hidden in this equation, expressed as a matrix:

\mathbf A_p = \mathbf O_c + \begin{bmatrix} \mathbf x_c & \mathbf y_c & \mathbf z_c \end{bmatrix} \begin{bmatrix} a \\ b \\c \end{bmatrix} \\ = \begin{bmatrix} x_{oc} & y_{oc} & z_{oc} \end{bmatrix} + \begin{bmatrix} x_{xc} & x_{yc} & x_{zc} \\ y _ {xc} & y _ {yc} & y _ {zc}\ z_ {xc} & z_ {yc} & z_ {zc}\\ \end{bmatrix} \begin{bmatrix} a \\ b \\c \end{bmatrix}

Then we convert it into a homogeneous coordinate representation:

\mathbf A_p = \begin{bmatrix} x_{oc} & y_{oc} & z_{oc} & 1 \end{bmatrix} + \begin{bmatrix} x_{xc} & x_{yc} & x_{zc} & 0 \\ y _ {xc} & y _ {yc} & y _ {zc} & 0\ z_ {xc} & z_ {yc} & z_ {zc} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\c \\ 1 \end{bmatrix} \\ = \begin{bmatrix} 1 & 0 & 0 & x_{oc} \\ 0 & 1 & 0 & y_{oc} \\ 0 & 0 & 1 & z_{oc} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x_{xc} & x_{yc} & x_{zc} & 0 \\ y _ {xc} & y _ {yc} & y _ {zc} & 0\ z_ {xc} & z_ {yc} & z_ {zc} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\c \\ 1 \end{bmatrix} \\ = \begin{bmatrix} x_{xc} & x_{yc} & x_{zc} & x_{oc} \\ y _ {xc} & y _ {yc} & y _ {zc} & y _ {oc}\ z_ {xc} & z_ {yc} & z_ {zc} & z_ {oc}\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\c \\ 1 \end{bmatrix} \\

Then our transformation matrix is

\begin{bmatrix} x_{xc} & x_{yc} & x_{zc} & x_{oc} \\ y _ {xc} & y _ {yc} & y _ {zc} & y _ {oc}\ z_ {xc} & z_ {yc} & z_ {zc} & z_ {oc}\\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} | & | & | & 0 \\ \mathbf x_c & \mathbf y_c & \mathbf z_c & \mathbf O_c \\ | & | & | & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

Model space

Model space, also known as local space or object space, each model has an independent coordinate space. When the model rotates, the coordinate space also rotates together.

In model space, we often use the natural direction of up, down, left, right, front, back and forth.

Since Unity uses a left-handed coordinate system, in model space, the positive directions of the coordinate axes of x, y, and z are the right, up, and forward directions of the model, respectively.

The origin and axes of the model space are set by the artist in the modeling software. When imported into Unity, we can access the vertex information of the model in the vertex shader, which contains the coordinates of each vertex, which are relative to the coordinate space of the model space.

World space

This space is the maximum space of the game, the so-called maximum is a macro concept, referring to the most peripheral space that the game can reach.

World space can be used to describe absolute position. Of course, position is relative, but here we define the position in the world space coordinate system as absolute position.

In Unity, the world space is also left-handed, but its coordinate axis is fixed.

In Unity, we can adjust the Transform property to change the position of the object relative to the parent object, or if there is no parent object, then relative to world space.

Model Transformation: From Model Space to World Space

Suppose there is a GameObject in our world space, and the three properties of its Transform component, Position, Rotation and Scale, are respectively, (5, 0, 25), (0, 150, 0) and (2, 2, 2), then according to the affine transformation matrix of the coordinate space we mentioned earlier is:

$$\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} cosθ & 0 & sinθ & 0 \\ 0 & 1 & 0 & 0 \\ -sinθ & 0 & cosθ & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} k_x & 0 & 0 & 0 \\ 0 & k_y & 0 & 0 \\ 0 & 0 & k_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\= \begin{bmatrix} 1 & 0 & 0 & 5 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 25 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} -0.886 & 0 & 0.5 & 0 \\ 0 & 1 & 0 & 0 \\ -0.5 & 0 & -0.886 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\= \begin{bmatrix} -1.732 & 0 & 1 & 5 \\ 0 & 2 & 0 & 0\\ -1 & 0 & -1.732 & 25 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Next, we can make this affine transformation matrix for the coordinates of each point in the model to perform spatial transformation.

There may be doubts here. The idea of solving this transformation matrix is different from the transformation matrix of coordinate space we just talked about. It is more like the basic transformation matrix we talked about at the beginning.

In fact, we think about it, the results of these two are the same. According to the idea of the coordinate space transformation matrix, we must first obtain the representation of the coordinate system of the model space in the world space according to the Transform attribute, and then obtain the transformation matrix. The results of the two are the same. The following is the way we solve the observation transformation matrix.

Observation space

Observation space is also called camera space. Observation space can be considered a special case of model space. The camera is a very special model among all models. Its model space is worth discussing separately.

Camera space determines the perspective we use to render the game. In observation space, the camera is located at the origin, and its coordinate axis is arbitrary. In Untiy, the observation space x-axis points to the right, the y-axis points up, and the z-axis points to the rear of the camera, which is different from model space and world space., because the camera space takes a right-handed coordinate system, which is aligned with the OpenGL tradition.

Observation Transformation: From World Space to Observation Space

In the previous step, we obtained the coordinates of the points on the model in world space through the model transformation. Now we need to transform these coordinates into the observation space. In order to obtain the transformation matrix of our step, we can have two methods:

Construct the transformation matrix from observation space to world space, and then solve its Inverse Matrix, which is the transformation matrix from world space to observation space.

• Imagine translating the entire observation space, coinciding its origin with the origin of world space, and the coordinate axes also coincide separately.

The first method is our previous method, let’s try the second method now

Assuming that the Transform property of the camera indicates that the camera rotates first by (30, 0, 0) in the world coordinate space, and then translates by (0, 10, -10), then in order to move the camera back to the initial state, what to do is to first translate back according to (0, -10, 10), and then rotate back (-30, 0, 0), expressed as a transformation matrix:

$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cosθ & -sinθ & 0 \\ 0 & sinθ & cosθ & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0.886 & 0.5 & 0\\ 0 & -0.5 & 0.886 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & -10\\ 0 & 0 & 0 & 10\\ 0 & 0 & 0 & 1 \end{bmatrix} \\= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0.886 & 0.5 & -3.66\\ 0 & -0.5 & 0.886 & 13.66\\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Then because our camera is right-handed, we invert all z components, so our final transformation matrix is:

$$\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0.886 & 0.5 & -3.66\\ 0 & 0.5 & -0.886 & -13.66\\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Cutting space

The clipping space, also called the homogeneous clipping space, and the matrix used for transformation is called the clipping matrix, also called the projection matrix.

The goal of clipping space is to make it easy to crop the render graph elements. The elements completely located in the space will be retained, the elements completely located outside the space will be eliminated, and the elements partially located in the space will be cropped. How is the scope defined? The answer is the visual cone.

An optic cone is an area of space that determines the amount of space the camera can see. The optic cone consists of six planes, also known as the crop plane.

There are two types of cones, one is orthogonal projection and the other is perspective projection.

Two of the six crop planes are special, called the near crop plane and the far crop plane, which determine the depth of space that the camera can see

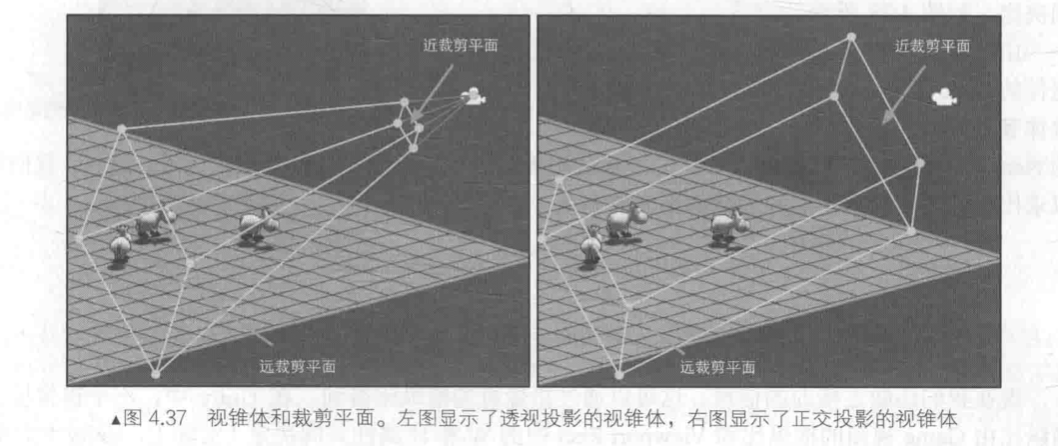
It can be seen that the visual cone of perspective projection is a pyramid shape, and the four cutting planes on the side intersect at the position of the camera. The orthogonal projection of the visual cone is a rectangular parallelepiped, and we hope to crop according to the scope of the visual cone, but if the space defined by the visual cone is directly used for cutting, then different visual cones will require different processing procedures, and for the visual cone of perspective projection, it is troublesome to judge whether a vertex is inside a pyramid. So we wanted to do the cropping in a more general, convenient, and neat way, by using a projection to transform the vertices into a cropping space.

The projection matrix has two purposes:

• Prepare for projection. This is a confusing point. Although it is called a projection matrix, it does not perform real projection work. It is preparing for projection. The real projection is the homogeneous division behind it. After the projection transformation, the w component has a special meaning.
• Scaling x, y, z, we said above that it is more troublesome to directly use the six clipping planes of the visual cone for clipping, but after the projection matrix, we can directly judge whether the x, y, z components are in the w component.

Perspective projection

We can change the opening angle of the viewing cone through FOV (Field of View), and the Near and Far properties in Clipping Planes control the distance between the main and far clipping planes of the near clipping bottle, which can calculate the height of the near clipping plane and the far clipping plane:

$$nearClipPlaneHeight = 2 * Near * tan \frac {FOV}2\\ farClipPlaneHeight = 2 * Far * tan \frac {FOV}2\\$$

Now we still lack the horizontal information, this can be obtained by the aspect ratio of the camera, in Unity, the aspect ratio of a camera is determined by the W and H in the View Port, assuming that our current aspect ratio is Aspect, then:

$$nearClipWidth = nearClipHeight * Aspect\\ farClipWidth = farClipHeight * Aspect\\$$

Then we can get the perspective projection matrix:

$$\begin{bmatrix} \frac {cot\frac{FOV}2}{Aspect} & 0 & 0 & 0\\ 0 & cot\frac{FOV}2 & 0 & 0\\ 0 & 0 & -\frac{Far + Near}{Far -Near} & -\frac{2*Far*Near}{Far -Near}\\ 0 & 0 & -1 & 0 \end{bmatrix}$$

After we use this matrix to transform the point in space:

$$\begin{bmatrix} \frac {cot\frac{FOV}2}{Aspect} & 0 & 0 & 0\\ 0 & cot\frac{FOV}2 & 0 & 0\\ 0 & 0 & -\frac{Far + Near}{Far -Near} & -\frac{2*Far*Near}{Far -Near}\\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x\frac {cot\frac{FOV}2}{Aspect}\\ ycot\frac{FOV}2\\ -z\frac{Far + Near}{Far -Near}-\frac{2*Far*Near}{Far -Near}\\ -z \end{bmatrix}$$

This matrix is built on the basis that Unity’s observation space is right-handed. Using this matrix to right-multiply the column matrix, the transformed z component will be between [-w, w].

As can be seen from the results, the matrix is scaled for the x and y components, and scaled and translated for the z component.

At this point, how do we determine whether a point is in the cone?

$$-w\ le x\ le w\\ -w\ le y\ le w\\ -w\ le z\ le w\\$$

It should also be noted that after cutting the matrix, the space will change from right-handed to left-handed.

Orthogonal projection

Orthogonal video cone is a rectangular parallelepiped, we can change the Size property to change half of the vertical height of the viewing cone, and the Near and Far properties of Cliping Plane control the distance between the near and far cutting planes, that is

$$farClipPlaneHeight = nearClipPlaneHeight = 2 * Size$$

The width of the apparent cone can be obtained by the aspect ratio

$$nearClipPlaneWidth = Aspect * nearClipPlaneHeight$$

Then the orthogonal projection matrix (clipping matrix) is:

$$\begin{bmatrix} \frac {1}{Aspect * Size} & 0 & 0 & 0 \\ 0 & \frac{1}{Size} & 0 & 0\\ 0&0&-\frac{2}{Far-Near}&-\frac{Far+Near}{Far-Near}\\ 0&0&0&1 \end{bmatrix}$$

Spatial transformation of points using this matrix:

$$\begin{bmatrix} \frac {1}{Aspect * Size} & 0 & 0 & 0 \\ 0 & \frac{1}{Size} & 0 & 0\\ 0&0&-\frac{2}{Far-Near}&-\frac{Far+Near}{Far-Near}\\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} x\\y\\z\\1 \end{bmatrix} = \begin{bmatrix} \frac {x}{Aspect * Size} \\ \frac{y}{Size} \\-\frac{2z}{Far-Near}-\frac{Far+Near}{Far-Near}\\1 \end{bmatrix}$$

Note that in the perspective matrix of orthogonal projection, the w component is still 1.

The way to determine whether a point is in an orthogonal projection is the same as a perspective projection, and this is why we need to deal with this projection transformation

Screen space

After the projection matrix transformation, we can crop, after the cutting work is completed, we can start the real projection, that is, the point in the cone is projected onto the screen, after this step, we will get the real pixel position.

The screen has a two-dimensional space, so we must project the vertices from the clipping space into the screen space to generate the corresponding 2D coordinates.

First, we need to perform the standard homogeneous division, that is, ** perspective division **, that is, divide x, y, z by the w component, respectively. In OpenGL, we call the coordinates obtained in this step Normalized Device Coordinate (NDC).

After this step, the clipping space of the perspective projection will become a cube. According to the OpenGL tradition, the x, y, and z components of this cube are all in the range [-1, 1], and DirectX is [0, 1], while the clipping space of the orthogonal projection itself is a cube, and its w component is 1, which will not have any effect on x, y, z.

Now all we have to do is to project the coordinates in this NDC to the screen. In Unity, the pixel coordinates in the lower left corner of the screen are (0,0), and the coordinates in the upper right corner are (pixelWidth, pixelHeight). Since the range of the current coordinates is [-1,1], so we need to scale.

The formulas for homogeneous division and scaling together are:

$$screen_x = \frac{clip_x * pixelWidth}{2 * clip_w}+\frac{pixelWidth}{2}\\ screen_y = \frac{clip_y * pixelWidth}{2 * clip_w}+\frac{pixelHeight}{2}\\$$

Only the x and y components were mentioned above, because the screen is a two-dimensional space, so what about the z component? Usually, the z component is used for depth buffers

Summary