Principles of Unity Rendering (9) Unity Lighting Model

Posted on Edited on In Waline:

We are officially starting to learn some Shaders that can be applied, this time we will start with the lighting model. The code and concepts in this article are interpreted from “Getting Started with Unity Shader Essentials”.

This article mainly explains the principles and code analysis of several lighting models in the book.

Illumination of the Real World - How We See the World

The purpose of the game world we build is to imitate a real world, so we need to mathematically model the principles of object imaging in the real world, and then use the program to realize this mathematical model.

So our first step before learning the Unity lighting model is to have a basic understanding of real-world lighting.

When we say “this object is red,” it’s actually because this object reflects more red light and absorbs all other colors of light waves, and an object is black, it actually absorbs all colors of light waves.

Generally speaking, to simulate real lighting to generate an image, we need to consider three physical phenomena:

  • First, the light is emitted from the light source
  • Then, the light and some objects in the scene meet, some light is absorbed by the object, and some light is scattered by the object in other directions.
    Finally, the camera absorbs some light and produces an image

Light source

Light is emitted by a light source. In real-time rendering, we usually treat the light source as a point with no volume and use ** l ** to represent its direction. So how do we measure how much light a light source emits? That is, how do we quantify a light? In optics, this is called irradiance. For parallel light, its irradiance can be obtained by calculating the energy passing through a unit area perpendicular to l. The surface of an object is generally not perpendicular to l. When calculating the irradiance of an object surface, we can calculate the cosine of the angle between the surface normal of the illumination direction l.

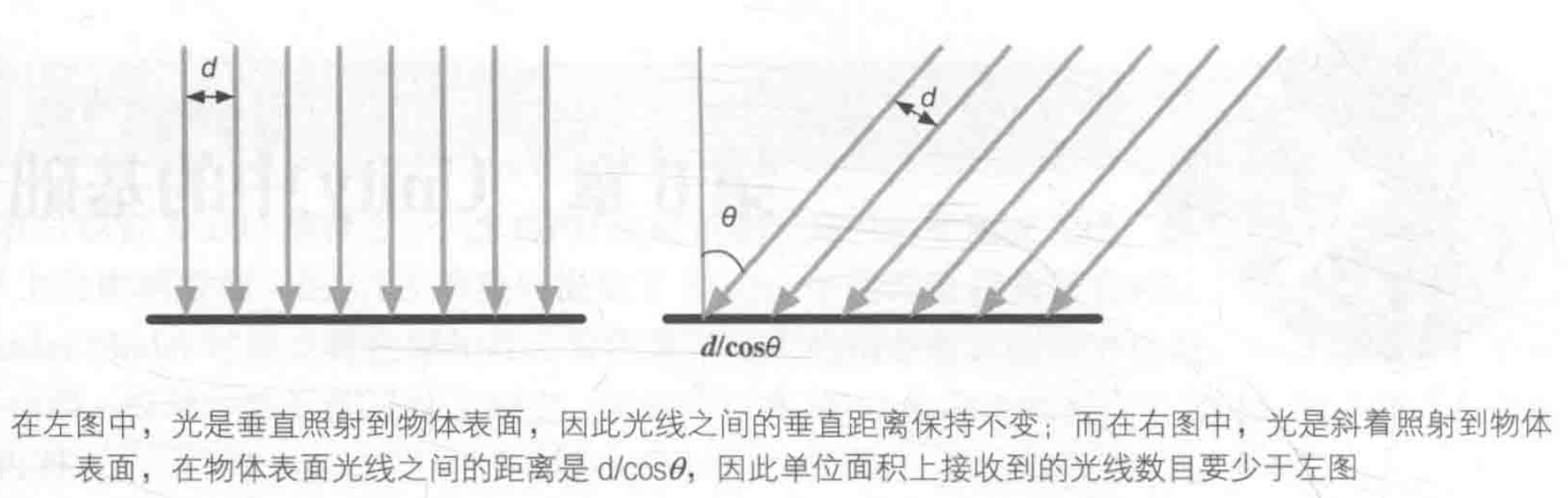
Since the irradiance is inversely proportional to the distance d/cosθ between the rays when they hit the surface of the object, the irradiance is proportional to cosθ. Cosθ can be obtained from the dot product of the light source direction l and the surface normal n.

Absorption and scattering

After the light is emitted by the light source, it intersects with the object. There are usually two results of intersection: scattering and absorption.

Scattering only changes the direction of the light without changing the density and color of the light. Absorption only changes the density and color of the light, but does not change the direction of the light.

After light is scattered on the surface of an object, there are two directions, one will scatter into the interior of the object, which is called refraction or transmission; the other will scatter to the outside, which is called reflection.

For opaque objects, the light rays refracted into the interior of the object may also continue to intersect the particles inside, with some of the light rays finally re-emitted from the surface of the object, and others absorbed by the object. Those rays re-emitted from the surface of the object will have a different directional distribution and color than the incident ray line.

In order to distinguish between these two different kinds of scattering, we use different parts of the lighting model to calculate them: specular, which indicates how light is reflected by an object, and diffuse, which indicates how much light will be refracted, absorbed, and scattered out of the surface.

Based on the number and direction of incident rays, we can calculate the number and direction of outgoing rays, which we usually use to describe it.

To sum up, there are two kinds of results of the intersection of light and objects: scattering and absorption, scattering is divided into refraction and reflection, reflection we use high light reflection to calculate, refraction with diffuse reflection to calculate.

Coloring

Shading refers to the process of using an equation to calculate the emissivity along a certain viewing direction according to material properties (such as diffuse emission properties, etc.) and light source information (such as light source direction, irradiance, etc.). ** We call this equation the lighting model (Lighting Mode) **, different lighting models have different purposes, some terms describe rough surfaces, and some are used to describe metal surfaces.

BRDF model

When light hits a surface from a certain direction, how much light is reflected and in what direction?

BRDF (Bidirectional Reflection Distribution Function) is the answer to this question. When given a point on the surface of the model, BRDF contains a complete description of the appearance of that point. In graphics, BRDF is mostly represented by a mathematical formula and provides a parameter to adjust the material properties.

Standard illumination model

There are many different lighting models, but in the early game engines, there was often only one lighting model used, which was called the standard lighting model. In fact, the standard lighting model was widely used before BRDF was proposed.

The standard lighting model only cares about direct light, that is, those rays that are emitted directly from the light source and illuminated on the surface of the object, and then directly enter the camera through a reflection from the surface of the object.

Its basic method is to divide the light entering the camera into four parts, each part using a method to calculate its contribution, these four parts are:

  • The emissive section. This section is used to describe how much radiation a surface emits in a given direction. Note that if global illumination is not used, these self-luminous surfaces do not actually illuminate surrounding objects, but only appear brighter themselves. For specific details, please refer to the official doc:发光材质 - Unity
  • Specular section. This section describes how much radiation the surface will scatter in the direction of full specular reflection when light from the light source hits the model surface.
  • Diffuse section. This section describes how much radiation the surface will scatter in all directions as light from the light source hits the model surface.
  • The ambient part. All other indirect lighting (as opposed to direct lighting).

Ambient light

While standard lighting models focus on describing direct illumination, in the real world, objects can also be illuminated by indirect illumination.

Indirect illumination is when light is reflected between multiple objects and finally enters the camera. For example, if you put a light gray sofa near the red carpet, the bottom of the sofa will also have red because the carpet reflects some of the light and bounces back onto the sofa.

In the standard lighting model, we use a part called ambient light to approximate indirect lighting. The calculation of ambient light is very simple, usually by setting a global variable, that is, all objects in the scene use this ambient light.

cambient=gambientc_{ambient} = g_{ambient}

Self-luminous

Light can also be emitted directly from the light source into the camera without being reflected by any object. The standard lighting model uses self-luminescence to calculate this contribution. Its calculation formula is also very simple, that is, the self-luminous color of the material is used.

cemissive=memissivec_{emissive} = m_{emissive}

Usually in real-time rendering, self-luminous surfaces often do not illuminate surrounding objects, that is, the object will not be used as a light source.

Diffuse reflection

Diffuse emission illumination is suitable for modeling the radiance of those objects whose surfaces scatter randomly in all directions. In diffuse emission, the position of the viewing angle is not important because the reflection is completely random, so the distribution can be considered the same in any reflection direction, but the angle of the incident ray is important.

Diffuse reflection is in accordance with Lambert’s Law: the intensity of the reflected light is proportional to the cosine of the angle between the surface discovery and the light source. Therefore, the calculation formula for the diffuse reflection part is:

cdiffuse=(clight⋅mdiffuse)max(0,n⋅I)c_{diffuse} = (c_{light} \cdot m_{diffuse})max(0, n \cdot I)

Where n is the surface normal, I is the unit vector of the light source, $m_ {diffuse} $is the diffuse color of the material, and $c_ {light} $is the color of the light source.
It should be noted that in order to prevent the normal and light source direction point multiplication result from being negative, we use the function of taking the maximum value to intercept it to 0, which can prevent the object from being illuminated by the light source from behind.

Here’s a question, why is it a dot product of two colors instead of adding them, and what is the result of multiplying two color values?
https://www.jianshu.com/p/70f5e349cd49

Highlight reflection

The specular reflection here is an empirical model, that is, it does not fully match the specular reflection phenomenon in the real world. It can be used to calculate the light that is reflected in the direction of full specular reflection, which can make objects look shiny, such as metal materials.

Calculate high light reflection need to know more information, such as surface normal, viewing angle direction, light source direction, reflection direction and so on.

We assume that these vectors are all unit vectors, and we can know three of these four vectors, and we can calculate the fourth - the reflection direction (the principle can refer to: https://blog.csdn.net/a1191835397/article/details/102779766)

r=2(n⋅I)n−Ir = 2(n \cdot I)n - I

In this way, we can use the Phong model to calculate the highlight reflection part:

cspecular=(clight⋅mspecular)max(0,v⋅r)mglossc_{specular} = (c_{light} \cdot m_{specular})max(0, v \cdot r)^{m_{gloss}}

Where $m_ {gloss} $is the gloss of the material, also known as shininess. It is used to control how wide the highlights are in the highlight area, the larger the $m_ {gloss} $, the smaller the highlights. $m_ {specular} $is the highlight reflection color of the material, which is used to control the color and intensity of the highlight reflection of the material, and $c_ {light} $is the color and intensity of the light source. At the same time, it is necessary to prevent the value of $v\ cdot r $from being negative.

Compared with the Phong model, Blinn proposes a simple modification method to obtain similar results. The idea is that in order to avoid calculating the reflection direction r, Blinn introduces a new vector h for this purpose, which is obtained by taking v and I. After averaging, it is normalized, i.e.:

h=v+I∣v+I∣h = \frac{v + I}{|v + I|}

Then the formula of the Blinn model is as follows:

cspeular=(clight⋅mspecluar)max(0,n⋅h)mglossc_{speular} = (c_{light} \cdot m_{specluar})max(0, n \cdot h)^{m_{gloss}}

In the hardware implementation, if the distance between the camera and the light source is far enough, the Blinn model will be faster than the Phong model. This is because at this time, it can be considered that v and I are both fixed values, so h will be a constant, but when v or When I is not fixed, the Phong model may be faster.

Note that the Phong model and the Blinn model are both empirical models, and one should not be considered more correct than the other.

Pixel by pixel or vertex by vertex

The math used for the basic lighting mode is given above, so where should we do these calculations? Generally speaking, we have two options, calculate in the slice shader, also known as pixel-by-pixel lighting, and calculate in the vertex shader, also known as vertex-by-vertex lighting.

In pixel-by-pixel lighting, we will get its normal on a per-pixel basis (it can be the difference between the normal values of the vertices, or it can be sampled from the normal texture), and then calculate the lighting model. This technique of interpolating vertex normals between patches is called Phong shading, also known as Phong interpolation or normal interpolation technique, which is different from the Phong lighting model we talked about before.

Corresponding to this is vertex-by-vertex illumination, also known as Gouraud shading, in vertex-by-vertex illumination, we calculate the illumination at each fixed point, then perform linear interpolation inside the render graph element, and finally output it as pixel color.

Since the number of vertices is often smaller than that of pixel trees, vertex-by-vertex illumination is often less computational than pixel-by-pixel illumination. However, since vertex-by-vertex illumination relies on linear interpolation to obtain pixel illumination, vertex-by-vertex illumination can be problematic when there are nonlinear calculations in the illumination model (such as when specular reflections).

Ambient Light and Self-Illumination in Unity

Most objects do not have self-luminous properties. It is also very simple to add self-luminous properties, just add the luminous color before the final color output of the chip shader.

How to Implement a Diffuse Lighting Model

Now we officially try to write a diffuse reflection Shader, the specific principle directly see the code comments

Vertex-by-vertex illumination

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
Shader "Unlit/DiffuseVertexLevel"
{
    Properties
    {
        //Declare a property for external incoming, type is Color, default value is white
        _Diffuse("Diffuse", Color) = (1,1,1,1)
    }
    SubShader
    {
        The render type is opaque object
        Tags { "RenderType"="Opaque" }
        // LOD（Leevl of Drtail）值时100
        LOD 100

        Pass
        {
            Tags{
                //Define the role of the Pass in Unity's pipeline (only by defining it can you get some of Unity's built-in lighting variables such as _LightColor0  
                //In the default pipeline, the lighting mode is ForwardBase etc
				"LightMode" = "UniversalForward"    
			}
            CGPROGRAM
            #include "Lighting.cginc"
            
            #pragma vertex vert
            #pragma fragment frag

            fixed4 _Diffuse;

            struct a2v
            {
                float4 vertex: POSITION;
                float3 normal: NORMAL;
            };

            struct v2f
            {
                float4 pos: SV_POSITION;
                fixed3 color: COLOR; 
            };

            v2f vert (a2v v)
            {
                v2f o;
                //Vertex shader must convert vertex coordinates from model space to clipping space
                o.pos = UnityObjectToClipPos(v.vertex);
                //get the value of ambient light
                fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;

                //The vertex normal is right multiplied by the world space to the model space matrix transformation matrix, and then normalized to obtain the vector of the vertex normal in the world coordinates
                fixed3 worldNormal = normalize(mul(v.normal, (float3x3)unity_WorldToObject));

                //When there is only one light source in the scene, the _ WorldSpaceLightPos0.xyz is the light source
                fixed3 worldLight = normalize(_WorldSpaceLightPos0.xyz);

                //dot: dot multiplication
                //saturate: If the imported parameter is less than 0, return 0. If it is greater than 1, return 1. Otherwise, return the original value.
                //The result of multiplying the pixel values is a color blend
                fixed3 diffuse = _LightColor0.rgb * _Diffuse.rgb * saturate(dot(worldNormal, worldLight));

                The result of adding pixel values is a color overlay
                o.color = ambient + diffuse;
                return o;
            }

            fixed4 frag(v2f i) : SV_Target {
                return fixed4(i.color, 1.0);
            }

            ENDCG
        }
    }
    
    Fallback "Diffuse"
}

Pixel-by-pixel illumination

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
Shader "Unlit/DiffusePixelLevel"
{
    Properties
    {
        _Diffuse("Diffuse", Color) = (1,1,1,1)
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            Tags{
                //Define the role of the Pass in Unity's pipeline (only by defining it can you get some of Unity's built-in lighting variables such as _LightColor0  
                //In the default pipeline, the lighting mode is ForwardBase etc
				"LightMode" = "UniversalForward"    
			}
            CGPROGRAM
            #include "Lighting.cginc"
            
            #pragma vertex vert
            #pragma fragment frag

            fixed4 _Diffuse;

            struct a2v
            {
                float4 vertex: POSITION;
                float3 normal: NORMAL;
            };

            struct v2f
            {
                float4 pos: SV_POSITION;
                float3 worldNorma: TEXCOORD0;
            };

            v2f vert (a2v v)
            {
                v2f o;
                o.pos = UnityObjectToClipPos(v.vertex);
                o.worldNorma = mul(v.normal, (float3x3)unity_WorldToObject);
                return o;
            }

            fixed4 frag(v2f i) : SV_Target {
                fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;
                fixed3 worldNormal = normalize(i.worldNorma);
                fixed3 worldLightDir = normalize(_WorldSpaceLightPos0.xyz);
                fixed3 diffuse = _LightColor0.rgb * _Diffuse.rgb * saturate(dot(worldNormal, worldLightDir));

                fixed3 color = ambient + diffuse;
                return fixed4(color, 1.0);
            }

            ENDCG
        }
    }
    
    Fallback "Diffuse"
}

How to Implement a Highlight Reflection Lighting Model

Vertex by vertex

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
Shader "Unlit/SpecularVertexLevel"
{
    Properties
    {
        _Diffuse("Diffuse", Color) = (1,1,1,1)
        _Specular("Specular", Color) = (1,1,1,1)
        _Gloss("Gloss", Range(8.0, 256)) = 20
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            Tags{"LightMode" = "UniversalForward"}
            CGPROGRAM
            #include "Lighting.cginc"
            #pragma vertex vert
            #pragma fragment frag

            fixed4 _Diffuse;
            fixed4 _Specular;
            float _Gloss;

            struct a2v
            {
                float4 vertex: POSITION;
                float3 normal: NORMAL;
            };

            struct v2f
            {
                float4 pos: SV_POSITION;
                float3 color: COLOR;
            };

            v2f vert(a2v v)
            {
                v2f o;

                o.pos = UnityObjectToClipPos(v.vertex);

                fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;

                fixed3 worldNormal = normalize(mul(v.normal, (fixed3x3)unity_WorldToObject));

                fixed3 worldLightDir = normalize(_WorldSpaceLightPos0.xyz);

                fixed3 diffuse = _LightColor0.rgb * _Diffuse.rgb * saturate(dot(worldNormal, worldLightDir));

                fixed3 reflectDir = normalize(reflect(-worldLightDir, worldNormal));

                fixed3 viewDir = normalize(_WorldSpaceCameraPos.xyz - mul(unity_ObjectToWorld, v.vertex).xyz);

                fixed3 specular = _LightColor0.rgb * _Specular.rgb * pow(saturate(dot(reflectDir, viewDir)), _Gloss);

                o.color = ambient + diffuse + specular;

                return o;
            }

            fixed4 frag(v2f i) : SV_Target {
                return fixed4(i.color, 1.0);
            }
            ENDCG
        }
    }
    
    Fallback "Specular"
}

Pixel by pixel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
Shader "Unlit/SpecularPixelLevel"
{
    Properties
    {
        _Diffuse("Diffuse", Color) = (1,1,1,1)
        _Specular("Specular", Color) = (1,1,1,1)
        _Gloss("Gloss", Range(8.0, 256)) = 20
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            Tags{"LightMode" = "UniversalForward"}
            CGPROGRAM
            #include "Lighting.cginc"
            #pragma vertex vert
            #pragma fragment frag

            fixed4 _Diffuse;
            fixed4 _Specular;
            float _Gloss;

            struct a2v
            {
                float4 vertex: POSITION;
                float3 normal: NORMAL;
            };

            struct v2f
            {
                float4 pos: SV_POSITION;
                float3 worldNormal: TEXCOORD0;
                float3 worldPos: TEXCORRD1;
            };

            v2f vert(a2v v)
            {
                v2f o;

                o.pos = UnityObjectToClipPos(v.vertex);

                o.worldNormal = mul(v.vertex, (float3x3)unity_WorldToObject);

                o.worldPos = mul(unity_ObjectToWorld, v.vertex).xyz;

                return o;
            }

            fixed4 frag(v2f i) : SV_Target {
                fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;

                fixed3 worldNormal = normalize(i.worldNormal);

                fixed3 worldLightDir = normalize(_WorldSpaceLightPos0.xyz);

                fixed3 diffuse = _LightColor0.rgb * _Diffuse.rgb * saturate(dot(worldNormal, worldLightDir));

                fixed3 reflectDir = normalize(reflect(-worldLightDir, worldNormal));

                fixed3 viewDir = normalize(_WorldSpaceCameraPos.xyz - i.worldPos.xyz);

                fixed3 specular = _LightColor0.rgb * _Specular.rgb * pow(saturate(dot(reflectDir, viewDir)), _Gloss);

                return fixed4(ambient + diffuse + specular, 1.0);

            }
            ENDCG
        }
    }
    
    Fallback "Specular"
}