Principles of Unity Rendering (16) Unity Cube Textures

Posted on Edited on In Waline:

The textures we used before, such as normal textures, gradual change textures, mask textures, etc., are all one-dimensional or two-dimensional. This time we will introduce the cube texture and see how to use the cube texture to achieve environment mapping.

In graphics, Cubemap is an implementation of Environment Mapping. Environment mapping can simulate the environment around an object, and objects using environment mapping can appear to reflect the surrounding environment as if they were plated with metal.

The cube texture contains a total of six images, which correspond to the six faces of a cube, hence the name of the cube texture. Each face of the cube represents the image obtained by observing along the axis (up, down, left, right, front, and back) below the world space.

So how do we sample this texture? Unlike the 2D texture coordinates used before, for cube texture sampling we need to provide a 3D texture coordinate, and this ** 3D texture coordinate represents a 3D direction in world space. This vector is emitted from the center of the cube, and when it extends outward, it will intersect with one of the six textures of the cube, and the sampling result is calculated from this intersection point.

The advantage of the cube texture is that it is simple and fast to implement, and the effect is better. However, there are some drawbacks, such as introducing new objects into the scene, when the light source or object moves, we need to regenerate the cube texture. In addition, the cube texture can only reflect the environment, but not the object itself using the cube texture. This is because the cube texture cannot touch the result of multiple reflections, such as when two metal balls reflect each other.

Cube textures have many applications in real-time rendering, the most common being skybox.

Sky Box

Skybox is a method used in games to simulate backgrounds. The name Skybox also contains two pieces of information: it is used to simulate the sky, and secondly it is a box. When we use Skybox in a scene, our entire scene is surrounded by a cube. The technology used for each face of this cube is ** cube texture mapping technology **.

The use of the skybox is relatively simple, so I won’t go into details. The main thing is that the WrapMode of the six maps selects Clamp to prevent mismatch at the seams due to accuracy problems.

How to create a cube texture

In Unity 5, there are three ways to create cube textures for environment mapping:

  • Created directly from some special layout texture. This texture can be roughly imagined as the texture itself is the layout of the cube expansion.
  • Manually create a Cubemap resource and assign six images to it
  • The third method is script generation

Unity officially recommends using the first method, which compresses texture data and supports edge correction, glossy reflection, and HDR

The first two methods require us to prepare the image of the cube texture in advance, and the cube texture we get is often shared by the objects in the scene. Ideally, we want to generate different cube textures depending on the position of the object in the scene. This is, we can use scripts to create it in Unity. This is achieved by using the’Camera. RenderToCubemap 'function provided by Unity. This function can store the scene image seen from any location into six images, thereby creating the corresponding cube texture at that location.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
using UnityEditor;
using UnityEngine;

namespace Tools.Scripts.CreateCubemap
{
    public class CreateCubemap: ScriptableWizard
    {
        public Cubemap cubemap;
        public Transform renderFromPosition;
        [MenuItem("Tools/CreateCubemap")]
        public static void Create()
        {
            ScriptableWizard.DisplayWizard<CreateCubemap>("CreateCubemap", "Create");
        }
        
        void OnWizardCreate() {
            GameObject go = new GameObject("CubemapCamera");
            go.AddComponent<Camera>();
            go.transform.position = renderFromPosition.position;
            go.GetComponent<Camera>().RenderToCubemap(cubemap);
            DestroyImmediate(go);
        }
    }
}

In the above code, we create a camera at the renderFromPosition position and call the RenderToCubemap function to render the currently observed image into the user-specified cube texture, and then destroy it after completion.

It is also very simple to use:

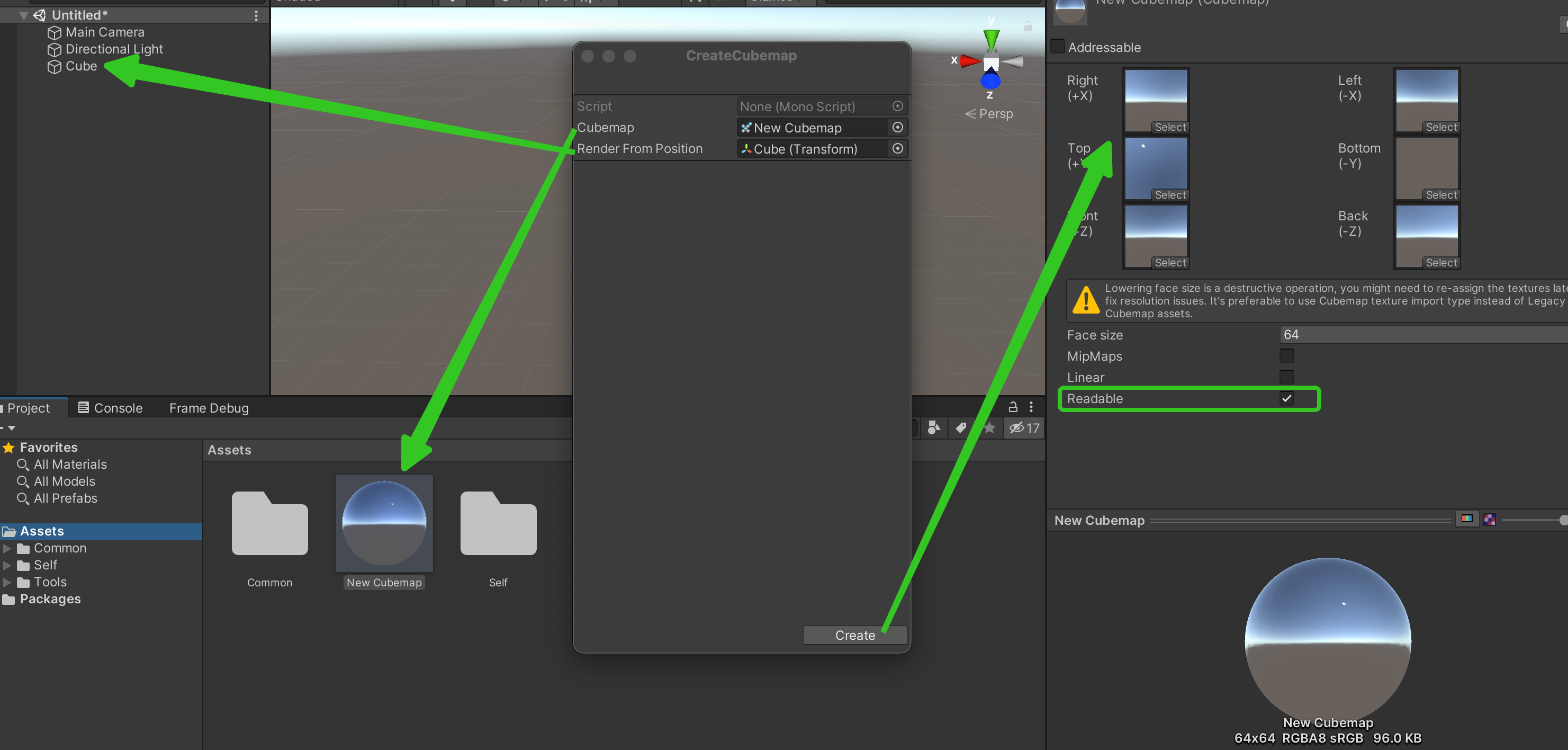
  • This code will add a menu item to the editor menu, we can click “Tools- > CreateCubemap” to bring up the panel
  • Then right-click “Create - > Legacy - > Cubemap” in Project to create a Cubemap, and check ** Readable ** in the panel, and assign it to the cubemap variable on the panel
    Create a gameobject in the scene and assign it to the renderFromPosition variable of the panel
  • Click the Create button

Then we can get the environment texture as seen from the gameobject location.

Once created, we can use environment mapping techniques. The most common environment mapping techniques are reflection and refraction.

Reflection

Objects that use the reflection effect usually look like they are plated with metal. To simulate the reflection effect is very simple, you only need to calculate the reflection direction by the direction of the incident ray and the surface method display direction, and then use the reflection direction to sample the cube texture.

We need to make the following preparations:

  • Create a new scene and replace the skybox of the new scene with the Cubemap we just generated
  • Drag a Teapot into the scene at the same location as the gameobject we used to generate the Cubemap in the previous step
  • Create a new material, named ReflectionMat, and assign the material to the Teapot model
  • Create a new Shader, named Reflection and assign it to the material created in the previous step

The reflected Shader is relatively simple and can be divided into the following steps:

(1) Declare new attributes:

1
2
3
4
5
6
Properties {
    _Color("Color Tint", Color) = (1,1,1,1)
    _ReflectColor("Reflection Color", Color) = (1,1,1,1)
    _ReflectAmount("Reflect Amount", Range(0,1))  = 1
    _Cubemap("Reflection Cubemap", Cube) = "_Skybox"{}
}

(2) Calculate the reflection direction at this point in the vertex shader, we directly use the reflect function of CG to calculate

1
2
3
4
5
6
7
8
9
10
v2f vert(a2v v) {
    v2f o;
    o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
    o.worldNormal = UnityObjectToWorldNormal(v.normal);
    o.worldPos = mul(unity_Object2World, v.vertex).xyz;
    o.worldViewDir = UnityWorldSpaceViewDir(o.worldPos);
    o.worldRefl = reflect(-o.worldViewDir, o.worldNormal);
    TRANSFER_SHADOW(o);
    return o;
}

(3) Sampling by reflection direction in chip element shader

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
fixed4 frag(v2f i): SV_Target {
    fixed3 worldNormal = normalize(i.worldNormal);
    fixed3 worldLightDir = normalize(UnityWorldSpaceLightDir(i.worldPos));
    fixed3 worldViewDir = normalize(i.worldViewDir);

    fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;

    fixed3 diffuse = _LightColor0.rgb * _Color.rgb * max(0, dot(worldNormal, worldLightDir));

    fixed3 reflection = texCUBE(_Cubemap, i.worldRefl).rgb * _ReflecColor.rgb;

    UNITY_LIGHT_ATTENUATION(atten, i, i.worldPos);

    fixed3 color = ambient + lerp(diffuse, reflection, _ReflectAmount) * atten;
    
    return fixed4(color, 1.0);
}

Refraction

In this section, we will learn how to simulate another common application of environment mapping in Unity Shader - refraction.

The physics of refraction is a little more complicated than reflection. We have been dealing with the definition of refraction since junior high school physics; when light is incident obliquely from one medium to another, the direction of propagation generally changes. When given the angle of incidence, we can use Snell’s theorem to calculate the reflection angle. When light enters medium 2 from medium 1 at an angle of $θ _1 $to the surface normal, the angle between the refracted light and the normal can be calculated using the following formula $θ _2 $

n1sinθ1=n2sinθ2n_1sinθ_1 = n_2sinθ_2

$n_1 $and $n_2 $are the refractive indices of the two media, respectively, and the refractive index is an important physical constant.

Normally, once we have the refraction direction, we will use it directly to sample the cube texture, but this is not in accordance with the laws of physics. For a transparent object, a more accurate simulation method requires calculating two refractions - one when light enters its interior and the other when it exits from its interior. However, simulating the second refraction direction in real-time rendering is more complicated, and simulating the effect obtained only once seems to be no problem, so we usually only simulate the first refraction.

We first need to do a similar preparation to the previous section on reflection, this time we call the Shader Refraction

(1) Declare new attributes:

1
2
3
4
5
6
7
Properties {
    _Color("Color Tint", Color) = (1,1,1,1)
    _RefractColor("Refraction Color", Color) = (1,1,1,1)
    _ReflractAmount("Refraction Amount", Range(0,1))  = 1
    _ReflractRatio("Refraction Ratio", Range(0,1))  = 1
    _Cubemap("Reflection Cubemap", Cube) = "_Skybox"{}
}

(2) Calculate the direction of refraction at the point in the vertex shader. We use the refract function to calculate the direction of refraction. Its first parameter is the direction of the incident ray line, which must be a normalized vector; The second parameter is the surface normal, and the normal direction is also normalized when needed. The third parameter is the ratio between the refractive index of the medium where the incident ray line is located and the refractive index of the ring where the refracted light is located

1
2
3
4
5
6
7
8
9
10
v2f vert(a2v v) {
    v2f o;
    o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
    o.worldNormal = UnityObjectToWorldNormal(v.normal);
    o.worldPos = mul(unity_Object2World, v.vertex).xyz;
    o.worldViewDir = UnityWorldSpaceViewDir(o.worldPos);
    o.worldRefr = refract(-normalize(o.worldViewDir), normalize(o.worldNormal), _ReflractRatio);
    TRANSFER_SHADOW(o);
    return o;
}

(3) Sampling by using the refraction direction in the chip element shader

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
fixed4 frag(v2f i): SV_Target {
    fixed3 worldNormal = normalize(i.worldNormal);
    fixed3 worldLightDir = normalize(UnityWorldSpaceLightDir(i.worldPos));
    fixed3 worldViewDir = normalize(i.worldViewDir);

    fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;

    fixed3 diffuse = _LightColor0.rgb * _Color.rgb * max(0, dot(worldNormal, worldLightDir));

    fixed3 refraction = texCUBE(_Cubemap, i.worldRefr).rgb * _RefractColor.rgb;

    UNITY_LIGHT_ATTENUATION(atten, i, i.worldPos);

    fixed3 color = ambient + lerp(diffuse, refraction, _RefractAmount) * atten;
    
    return fixed4(color, 1.0);
}

Fresnel reflection

In real-time rendering, we often use Fresnel reflection to control the degree of reflection according to the viewing angle direction. Generally speaking, Fresnel reflection describes an optical phenomenon, that is, when light shines on the surface of an object, part of it is reflected, and part of it enters the object and is refracted or scattered.

There is a certain ratio between the reflected light and the incident ray, which can be calculated by Fresnel’s equation. An often used example is that standing by the lake and looking directly at the water surface at your feet, you will find that the water is almost transparent, and you can directly see the small fish and stones at the bottom of the water; but when you look up and see the water surface in the distance, you will find that you can hardly see the underwater scene, but only see the reflected environment of the water surface. This is the so-called Fresnel effect.

So how to calculate Fresnel reflection? You need to use the Fresnel equation. The Fresnel equation in the real world is very complicated, but in real-time rendering we usually use some approximation formula, such as ** Schlick Fresnel approximation equation **.

Fschlick(v,n)=F0+(1−F0)(1−v∗n)5F_{schlick}(v, n) = F_0 + (1 - F_0)(1 - v * n)^5

Where $F_0 $is a reflection coefficient that controls the intensity of the Fresnel reflection, v is the viewing angle direction, and n is the direction of the surface normal.

Another equation that is more widely used is the Emprurine Fresnel approximation equation.

FEmpricial(v,n)=max(0,min(1,bias+scale∗(1−v∗n)power))F_{Empricial}(v,n) = max(0, min(1, bias + scale * (1 - v * n)^{power}))

Among them, bias, scale, and power are all controls.

Let’s try a Shader of Schlick Fresnel’s approximation of the equation

(1) Declare new attributes:

1
2
3
4
5
Properties {
    _Color("Color Tint", Color) = (1,1,1,1)
    _FrenelScale("Fresnel Scale", Range(0,1))  = 0.5
    _Cubemap("Reflection Cubemap", Cube) = "_Skybox"{}
}

(2) Calculate the reflection direction, normal direction, and viewing angle direction at this point in the vertex shader. We directly use the reflect function of CG to calculate

1
2
3
4
5
6
7
8
9
10
v2f vert(a2v v) {
    v2f o;
    o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
    o.worldNormal = UnityObjectToWorldNormal(v.normal);
    o.worldPos = mul(unity_Object2World, v.vertex).xyz;
    o.worldViewDir = UnityWorldSpaceViewDir(o.worldPos);
    o.worldRefl = reflect(-o.worldViewDir, o.worldNormal);
    TRANSFER_SHADOW(o);
    return o;
}

(3) Implement Fresnel reflection in a slice shader and mix diffuse and reflected illumination using the resulting values

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
fixed4 frag(v2f i): SV_Target {
    fixed3 worldNormal = normalize(i.worldNormal);
    fixed3 worldLightDir = normalize(UnityWorldSpaceLightDir(i.worldPos));
    fixed3 worldViewDir = normalize(i.worldViewDir);

    fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;

    UNITY_LIGHT_ATTENUATION(atten, i, i.worldPos);

    fixed3 reflection = texCUBE(_Cubemap, i.worldRefl).rgb;

    fixed3 fresnel = _FrenelScale + (1 - _FrenelScale) * pow(1 - dot(worldViewDir, worldNormal), 5);

    fixed3 diffuse = _LightColor0.rgb * _Color.rgb * max(0, dot(worldNormal, worldLightDir));


    fixed3 color = ambient + lerp(diffuse, reflection, saturate(fresnel)) * atten;
    
    return fixed4(color, 1.0);
}