Shortest path algorithm

Posted on Edited on In Waline:

Last week’s blog we discussed and implemented the topological sorting of graphs. This week we continue to learn another basic algorithm of graphs, the shortest path algorithm Dijkstra algorithm, and how to transform it into our usual navigation or games. The pathfinding algorithm used.

Priority queue (heap)

Since the Dijkstra algorithm needs to use the priority queue, so we first imitate the implementation of a heap form.

First, let me explain what a heap is:

  • The heap is a complete binary tree;

  • The value of each node in the heap must be greater than or equal to (or less than or equal to) the value of each node in its child tree.

How to implement a heap

To implement a heap, we first need to know what operations the heap supports and how to store a heap.

We all know that complete binary trees are more suitable for storing in arrays. Using arrays to store complete binary trees is very storage space-saving. Because we don’t need to store pointers to left and right sub-nodes, we can find the left and right sub-nodes and parent nodes of a node simply through the index of the array. ** This is also why we use heaps to implement priority queues.

How to insert elements

After inserting an element into the heap, we need to continue to satisfy two properties of the heap.

If we put the newly inserted element at the end of the heap, you can see the picture I drew, is it not in line with the characteristics of the heap? So, we need to adjust it to meet the characteristics of the heap again. We have a name for this process, which is called heapify.

There are actually two types of stacking, bottom-up and top-down. Here I first talk about the bottom-up stacking method.

We can compare the size of the newly inserted node to the parent node. If the size relationship between the sub-node and the parent node is not satisfied, we swap the two nodes. Keep repeating this process until the size relationship between the parent and child nodes is satisfied.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Heap {
    constructor(capacity) {
        this.n = capacity;
        this.a = new Array(capacity);
        this.count = 0;
    }

    swap(i, j) {
        const temp = this.a[i];
        this.a[i] = this.a[j];
        this.a[j] = temp;
    }

    add(data) {
        if (this.count >= this.n) {
            return;
        }
        this.count++;
        this.a[this.count] = data;
        let i = this.count;
        while(Math.floor(i / 2) > 0 && this.a[i] < this.a[Math.floor(i / 2)]) {
            this.swap(i, Math.floor(i / 2));
            i = Math.floor(i / 2);
        }
    }
}

Remove top element

From the second item of the heap definition, the value of any node is greater than or equal to (or less than or equal to) the value of the child tree node, we can find that the top element of the heap stores the maximum or minimum value of the data in the heap. Suppose we construct a large top heap, and the top element of the heap is the largest element.

After we delete the top element, we need to put the second largest element on the top of the heap, and the second largest element will definitely appear in the left and right sub-nodes. Then we iteratively delete the second largest node, and so on, until the leaf node is deleted.

However, the above method is easy to destroy the structure of the heap

In fact, we can solve this problem by changing our thinking a little bit. You can see the picture I drew below. We put the last node on top of the heap, and then use the same parent-child node comparison method. For those that do not satisfy the size relationship between parent and child nodes, swap the two nodes, and repeat the process until the size relationship between parent and child nodes is satisfied. This is the top-down stacking method.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Heap {
    constructor(capacity) {
        this.n = capacity;
        this.a = new Array(capacity);
        this.count = 0;
    }

    swap(i, j) {
        const temp = this.a[i];
        this.a[i] = this.a[j];
        this.a[j] = temp;
    }

    add(data) {
        if (this.count >= this.n) {
            return;
        }
        this.count++;
        this.a[this.count] = data;
        let i = this.count;
        while(Math.floor(i / 2) > 0 && this.a[i] < this.a[Math.floor(i / 2)]) {
            this.swap(i, Math.floor(i / 2));
            i = Math.floor(i / 2)
        }
    }

    update(data) {
        for(let i = 0; i < this.count; i++) {
            if (this.a[i].key = data.key) {
                this.a[i] = data;
                break;
            }
        }
    }

    poll() {
        if(this.count = 0) {
            return -1;
        }
        this.a[0] = this.a[this.count];
        this.count--;
        this.heapify();
    }

    heapify() {
        let i = 0;
        while(true) {
            let maxPos = i;
            if (i * 2 <= this.count && this.a[i] > this.a[i * 2]) {
                maxPos = i * 2;
            }
            if (i * 2 + 1 <= this.count && this.a[i] > this.a[i * 2 + 1]) {
                maxPos = i * 2 + 1;
            }
            if (maxPos = i) {
                break;
            }
            this.swap(i, maxPos);
            i = maxPos;
        }
    }
}

Dijkstra algorithm

First, a step diagram of the algorithm

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Graph {
    constructor(v) {
        this.v = v;
        this.adj = new Array(v).fill([]);
    }

    addEdge(s, t, w) {
        this.adj[s].push(new Edge(s, t, w));
    }

    dijkstra(s, t) {
        let predecessor = new Array(this.v);
        let vertexes = new Array(this.v);
        for(let i = 0; i < this.v; i++) {
            vertexes[i] = new Vertex(i, Number.MAX_SAFE_INTEGER);
        }
        let queue = new Heap(this.v);
        let inqueue = new Array(this.v).fill(false);
        vertexes[s].dist = 0;
        queue.add(vertexes[s]);
        inqueue[s] = true;
        while(!queue.isEmpty()) {
            const minVertex = queue.poll();
            if (minVertex.id = t) {
                break;
            }
            for(let i = 0; i < this.adj[minVertex.id].length; i++) {
                const edge = this.adj[minVertex.id][i];
                const nexeVertex = vertexes[edge.tid];
                if (minVertex.dist + edge.w < nexeVertex.dist) {
                    nexeVertex.dist = minVertex.dist + edge.w;
                    predecessor[nexeVertex.id] = minVertex.id;
                    if (inqueue[nexeVertex.id]) {
                        queue.update(nexeVertex);
                    } else {
                        queue.add(nexeVertex);
                        inqueue[nexeVertex.id] = true;
                    }
                }
            }
        }
        console.log(s);
        print(s, t, predecessor);

    }

    print(s, t, predecessor) {
        if (s = t) {
            return;
        }
        print(s, predecessor[t], predecessor);
        console.log(`->${t}`);
    }
}
class Edge {
    constructor(sid, tid, weight) {
        this.sid = sid;
        this.tid = tid;
        this.w = weight;
    }
}

class Vertex {
    constructor(id, dist) {
        this.id = id;
        this.dist = dist;
    }
}

The idea of the dijkstra algorithm is a bit like BFS. It traverses all the vertices it can reach from the starting vertex, and then updates the shortest path to these vertices in turn. After updating, it is added to the priority queue. Next, take out the current dist from the priority queue. The smallest vertex, then calculate all the vertices it can reach, update them in turn, and then repeat the above process continuously.

But in fact, it is not a complete BFS, because the priority queue is different from the ordinary queue, it will adjust the position of the data every time data is inserted, to ensure that the data in the head is the minimum value in the queue, not first in first out.

A * algorithm (simplified Dijkstra algorithm)

Have you ever played MMRPG games such as World of Warcraft and Legend of Swords and Fairies? In these games, there is a very important function, that is, the character automatically finds its way. When the character is in a certain position in the game map, we click on another relatively far position with the mouse, and the character will automatically walk around the obstacle. Having played so many games, I wonder if you have thought about how this feature is achieved?

Algorithm Parsing In fact, this is a very typical search problem. The starting point of the character is where he is now, and the ending point is where the mouse clicks. We need to find a path in the map from the starting point to the end point. This path bypasses all obstacles in the map, and seems to be a very smart move. The so-called “smart”, in general terms, means that the road you take should not be too winding. ** In theory, the shortest path is obviously the smartest move, and it is the optimal solution to this problem. **

** However, if the graph is very large, the execution of the Dijkstra shortest path algorithm will take a lot of time **. In real software development, we are faced with super large maps and massive pathfinding requests, and the execution efficiency of the algorithm is too low, which is obviously unacceptable.

In fact, for real software development problems such as travel route planning and game pathfinding, under normal circumstances, we do not need to find the optimal solution (that is, the shortest path). In the case of weighing the quality of route planning and execution efficiency, we only need to seek a suboptimal solution. So how to quickly find a suboptimal route that is close to the shortest route?

This fast path planning algorithm is the A * algorithm we are going to learn today. In fact, A * algorithm is an optimization and transformation of Dijkstra algorithm.

** The Dijkstra algorithm is somewhat similar to the BFS algorithm. Every time it finds the vertex closest to the starting point **, it expands outward. ** This idea of outward expansion is actually a bit blind **. Why do you say that? Let me give you an example to explain. The following graph corresponds to a real map. The position of each vertex in the map is represented by a two-dimensional coordinate (x, y), where x represents the abscissa and y represents the ordinate.

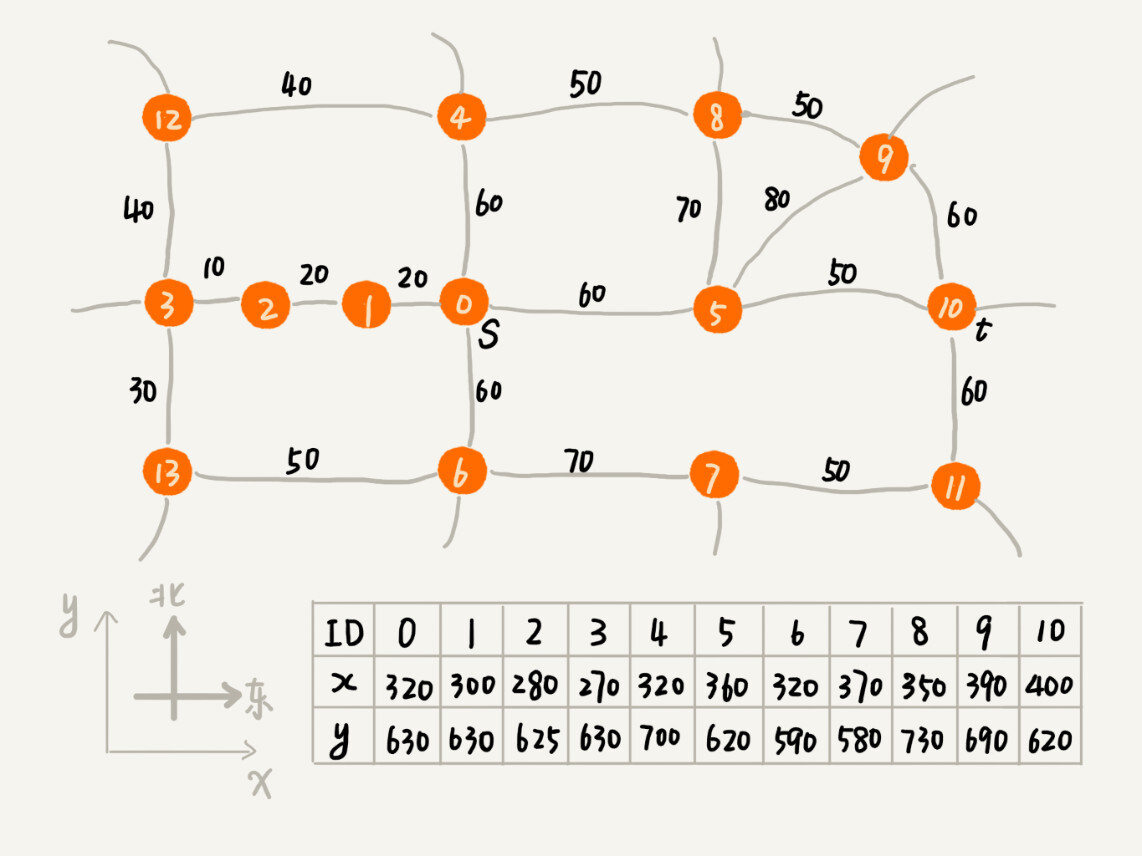
In the implementation idea of the Dijkstra algorithm, we use a priority queue to record the vertices that have been traversed and the path lengths of this vertex and the starting point. The smaller the length of the path between the vertex and the starting point, the more it will be taken out of the priority queue to expand. As can be seen from the example in the figure, although we are looking for the route from s to t, the first searched vertices are 1, 2, and 3 in turn. Observed with the naked eye, this search direction is opposite to our expected route direction (s to t is from west to east), and the route search direction is obviously “off”.

The reason why we “run off” is because we arrange the queue order according to the length of the path between the vertex and the starting point. The closer the vertex is to the starting point, the earlier it will be out of the queue. We didn’t take into account the distance from this vertex to the end point, so in the map, although the three vertices 1, 2, and 3 are closest to the starting vertex, they are getting farther and farther away from the end point.

If we combine more factors, take into account how far this vertex may have to go to the end point, and also take into account, and comprehensively judge which vertex should be out of the queue first, can we avoid “deviation”? When we traverse to a certain vertex, the length of the path from the starting point to this vertex is determined, which we record as g (i) (i represents the vertex number). However, the length of the path from this vertex to the end point is unknown. Although the exact value cannot be known in advance, we can use other estimates instead.

Here we can approximate the path length of this vertex and the end point by the straight-line distance between the vertex and the end point, that is, the Euclidean distance (note: path length and straight-line distance are two concepts). We denote this distance as h (i) (i represents the number of this vertex), and the professional name is heuristic function. Because the calculation formula of the Euclidean distance involves a relatively time-consuming square root calculation, we generally use another simpler distance calculation formula, which is the Manhattan distance. The Manhattan distance is the sum of the distances between two points in the abscissa and ordinate. The calculation process only involves addition and subtraction, sign bit inversion, so it is more efficient than the Euclidean distance.

Originally, it was only through the path length g (i) between the vertex and the starting point to judge who came out of the queue first. Now that we have the estimated value of the path length from the vertex to the end point, we use the sum of the two f (i) = g (i) + h (i) to judge which vertex should come out of the queue first. Combining the two parts, we can effectively avoid the “deviation” just mentioned. The professional name of f (i) here is the evaluation function. From the description just now, we can find that A * algorithm is a simple transformation of the Dijkstra algorithm. In fact, in terms of code implementation, we only need to slightly change a few lines of code to change the code implementation of the Dijkstra algorithm to the code implementation of the A * algorithm.

In the code implementation of the A * algorithm, the definition of the vertex Vertex class is slightly different from the definition in the Dijkstra algorithm, with the x, y coordinates, and the f (i) value just mentioned.

The main logic of the code implementation of A * algorithm is the following code. It differs from the code implementation of Dijkstra algorithm in three main points:

  • Priority queues are built in different ways. The A * algorithm builds priority queues based on the value of f (that is, f (i) = g (i) + h (i) just mentioned), while the Dijkstra algorithm builds priority queues based on the value of dist (that is, g (i) just mentioned);
  • A * algorithm will update the f value synchronously when updating the vertex dist value; the conditions for the end of the loop are also different.
  • Dijkstra algorithm is at the end of the queue when the end of the end, A * algorithm is once traversed to the end of the end.

Note:

All the figures in this article are from the Geek Time lesson “The beauty of data structures and algorithms”