Dynamic Programming

Posted on Edited on In Waline:

Recently, I encountered recursion when I was doing the question. I vaguely felt that it was a bit similar to the motion gauge, but I couldn’t explain it clearly, so I found a lot of articles. Here is an excerpt of the most basic but also the most clear article. The original link is这个。

Principle

The general form of Dynamic Programming problem is to find the best value. Dynamic Programming is actually an optimization method of operations research, but it is more used in computer problems, such as asking you to find the longest increasing sequence, the minimum editing distance, and so on.

Since it requires the most value, what is the core problem? The core problem of solving Dynamic Programming is exhaustion. Because the most value is required, you must exhaust all feasible answers and then find the most value among them.

Dynamic Programming is so simple, is it exhaustive? The Dynamic Programming problems I see are all very difficult!

First of all, the exhaustion of Dynamic Programming is a bit special, because there are “overlapping sub-problems” in this type of problem, and the efficiency will be extremely low if the brute force exhaustion is used, so “memo” or “DP table” is needed to optimize the exhaustion process and avoid unnecessary computation.

Moreover, the Dynamic Programming problem must have an “optimal substructure” in order to pass the most value of the subproblem to the most value of the original problem.

In addition, although the core idea of Dynamic Programming is to exhaust the maximum value, the problem can be ever-changing, and it is not an easy task to exhaust all feasible solutions. Only by listing the correct “state transition equation” can we correctly exhaust it.

The overlapping subproblems, optimal substructures, and state transition equations mentioned above are Dynamic Programming Three-factor Verification. What exactly it means will be explained in detail with examples, but in actual algorithm problems, writing state transition equations is the most difficult, which is why many friends find Dynamic Programming problems difficult. Let me provide a thinking framework I have researched to help you think about state transition equations:

Clear “state” - > define the meaning of dp array/function - > clear “selection” - > clear base case.

The following explains the basic principles of Dynamic Programming through the Fibonacci sequence problem and the change problem. The former is mainly to let you understand what an overlapping subproblem is (Fibonacci sequence is not strictly a Dynamic Programming problem), and the latter mainly focuses on how to list state transition equations.

Readers are asked not to dismiss the simplicity of this example. Only simple examples can allow you to fully focus on the general ideas and techniques behind the algorithm, without being confused by those obscure details. For difficult examples, there are historical articles.

Example

Fibonacci sequence

1 The recursion of violence

The mathematical form of the Fibonacci sequence is recursion, written in code like this:

1
2
3
4
int fib(int N) {
    if (N  1 || N  2) return 1;
    return fib(N - 1) + fib(N - 2);
}

Needless to say, school teachers seem to use this example when they talk about recursion. We also know that writing code like this is concise and easy to understand, but it is very inefficient. Where is the inefficiency? Assuming n = 20, please draw a recursion tree.

PS: Whenever you encounter a problem that requires recursion, it is best to draw a recursion tree, which will be of great help to you in analyzing the complexity of the algorithm and finding the reasons for the inefficiency of the algorithm.

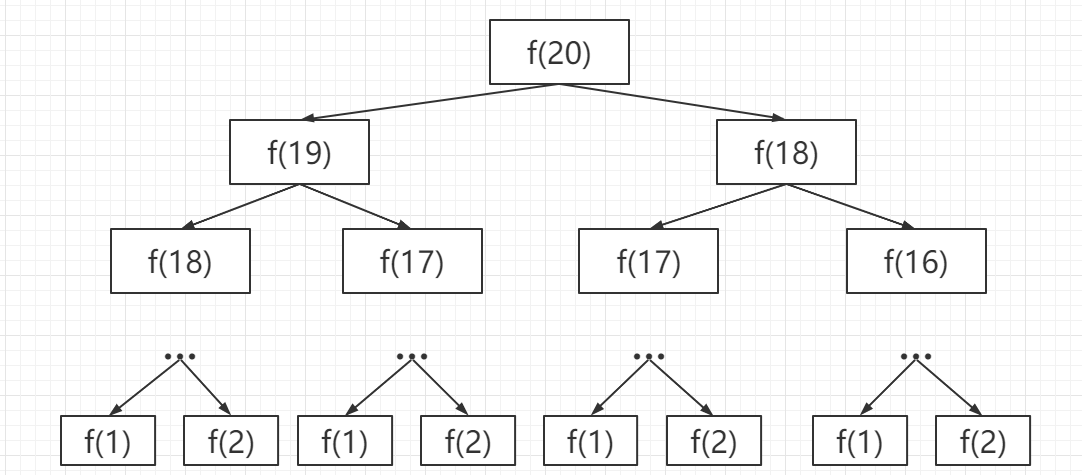
https://res.cloudinary.com/dvtfhjxi4/image/upload/v1608033289/origin-of-ray/微信截图_20201215195409_kdnd5s.png

How to understand this recursion tree? That is to say, if I want to calculate the original problem f (20), I have to first calculate the sub-problems f (19) and f (18), and then to calculate f (19), I have to first calculate the sub-problems f (18) and f (17), and so on. When you finally encounter f (1) or f (2), the result is known, and you can return the result directly, and the recursion tree will no longer grow downward.

How to calculate the time complexity of recursion algorithm? The number of subproblems multiplied by the time required to solve a subproblem.

The number of subproblems, that is, the total number of nodes in the recursion tree. Obviously, the total number of binary tree nodes is exponential, so the number of subproblems is O (2 ^ n).

The time to solve a subproblem, in this algorithm, there are no loops, only f (n - 1) + f (n - 2) an addition operation, and the time is O (1).

So, the time complexity of this algorithm is O (2 ^ n), exponential level, explosion.

Observing the recursion tree, it is obvious to find the reason for the inefficiency of the algorithm: there are a lot of repeated calculations, such as f (18) being calculated twice, and you can see that the recursion tree with f (18) as the root is huge, It will take a lot of time to calculate it again. What’s more, it’s not just the node f (18) that is repeatedly calculated, so this algorithm is extremely inefficient.

This is the first property of the Dynamic Programming problem: the overlapping subproblem. Below, we find a way to solve this problem.

  1. Recursion solution with memo

If you clarify the problem, you have already solved half of the problem. Since the reason for the time-consuming is repeated calculation, then we can make a “memo” and don’t rush to return after calculating the answer to a certain sub-problem every time, write it down in the “memo” and then return; every time you encounter a sub-problem, go to the “memo” first Check it out. If you find that the problem has been solved before, take out the answer directly and use it instead of spending time calculating.

Usually an array is used as this “memo”, of course you can also use a hash table (dictionary), the idea is the same.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int fib(int N) {
    if (N < 1) return 0;
    //Memo is all initialized to 0
    vector<int> memo(N + 1, 0);
    //initialize the simplest case
    return helper(memo, N);
}

int helper(vector<int>& memo, int n) {
    // base case 
    if (n  1 || n  2) return 1;
    //already calculated
    if (memo[n] != 0) return memo[n];
    memo[n] = helper(memo, n - 1) + 
                helper(memo, n - 2);
    return memo[n];
}

Now, draw the recursion tree and you’ll know what the memo does.

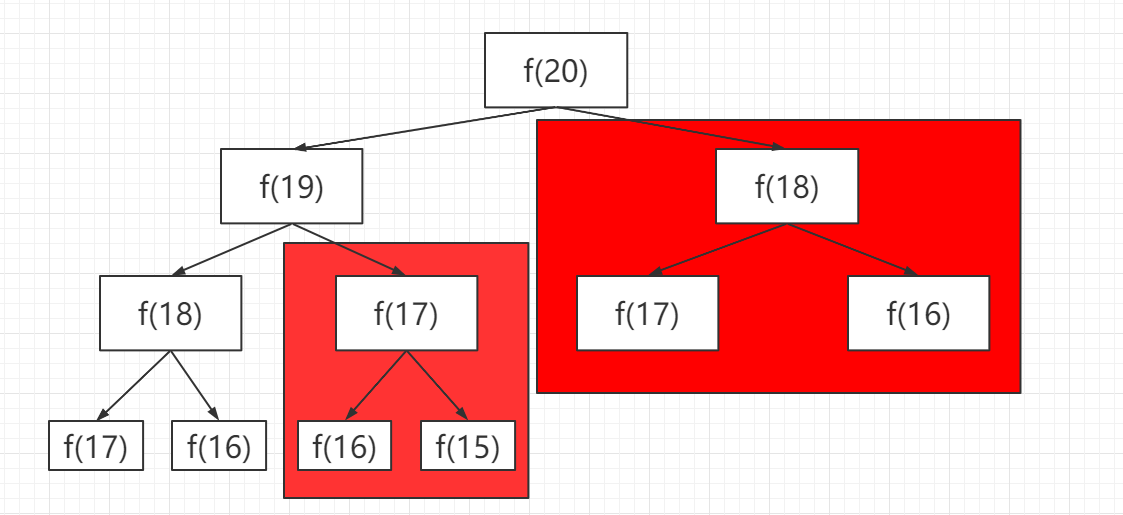
https://res.cloudinary.com/dvtfhjxi4/image/upload/v1608033688/origin-of-ray/微信截图_20201215200116_wqfxvd.png

In fact, the recursion algorithm with “memo” transforms a recursion tree with huge redundancy into a recursion graph without redundancy by “pruning”, which greatly reduces the number of sub-problems (that is, nodes in the recursion graph).

How to calculate the time complexity of the recursion algorithm? Multiply the number of subproblems by the time required to solve a subproblem.

The number of sub-problems, that is, the total number of nodes in the graph, since there is no redundant calculation in this algorithm, the sub-problems are f (1), f (2), f (3)… f (20), and the number is proportional to the input scale n = 20, so the number of sub-problems is O (n).

The time to solve a subproblem, as above, there is no loop, and the time is O (1).

Therefore, the time complexity of this algorithm is O (n). Compared with the brute force algorithm, it is a dimensionality reduction blow.

At this point, the efficiency of the recursion solution with memos is the same as that of the iterative Dynamic Programming solution. In fact, this solution is almost the same as the iterative Dynamic Programming solution, but this method is called “top-down” and Dynamic Programming is called “bottom-up”.

What is “top-down”? Note that the recursion tree (or graph) we just drew extends from top to bottom, starting from a large-scale original problem such as f (20), gradually decomposing the scale downward, Until f (1) and f (2) reach the bottom, and then return the answer layer by layer, this is called “top-down”.

What is “bottom-up”? In turn, we directly start from the bottom, the simplest, and the smallest problem size f (1) and f (2), and push up until we reach the answer f (20) we want. This is the idea of Dynamic Programming, which is why Dynamic Programming generally deviates from recursion, but completes the calculation by loop iteration.

  1. Iterative solution of dp array

With the inspiration of the previous “memo”, we can separate this “memo” into a table, called DP table, on this table to complete the “bottom-up” calculation is not beautiful!

1
2
3
4
5
6
7
8
int fib(int N) {
    vector<int> dp(N + 1, 0);
    // base case
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];
}

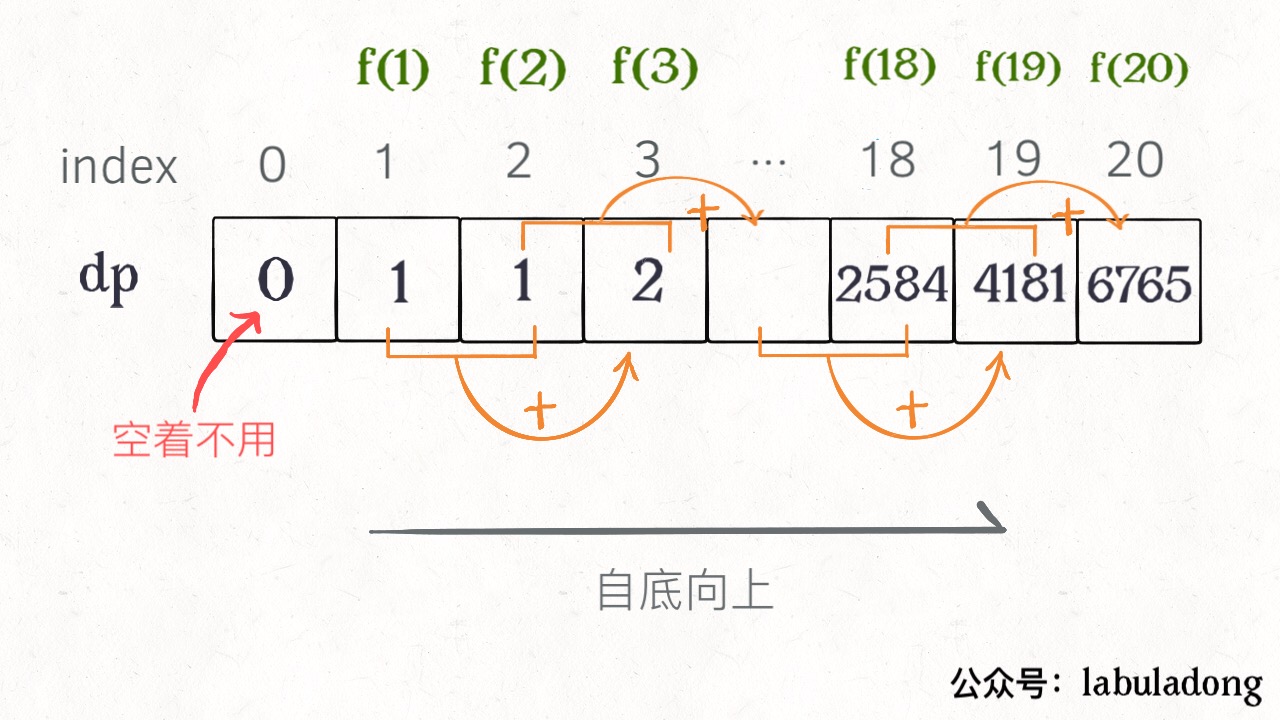
Drawing a picture is easy to understand, and you find that this DP table is very similar to the result after the “pruning” before, but the other way around. In fact, the “memo” in the recursion solution with memos is the DP table after the final completion, so the two solutions are actually similar, and in most cases, the efficiency is basically the same.

Here, the term “state transition equation” is introduced, which is actually a mathematical form describing the structure of the problem:

f(n) = 1, n = 1, 2

f(n) = f(n -1) + f(n -2), n >2

Why is it called the “state transition equation”? To sound high-end. You think of f (n) as a state n, which is transferred from the addition of state n - 1 and state n - 2, which is called state transition, nothing more.

You will find that all operations in the above several solutions, such as return f (n - 1) + f (n - 2), dp [i] = dp [i - 1] + dp [i - 2], and The initialization operation of the memo or DP table revolves around different representations of this equation. You can see the importance of listing the “state transition equation”, which is the core of solving the problem. It is easy to find that in fact, the state transition equation directly represents a brute force solution.

Never look down on the brute force solution. The most difficult thing about Dynamic Programming problems is to write the state transition equation, that is, the brute force solution. The optimization method is nothing more than using memos or DP tables, and there is no mystery at all.

At the end of this example, let’s talk about a detailed optimization. Careful readers will find that according to the state transition equation of the Fibonacci sequence, the current state is only related to the previous two states. In fact, it is not necessary to have such a long DP table to store all the states, just find a way to store the previous two states. Therefore, it can be further optimized to reduce the space complexity to O (1):

1
2
3
4
5
6
7
8
9
10
11
int fib(int n) {
    if (n  2 || n  1) 
        return 1;
    int prev = 1, curr = 1;
    for (int i = 3; i <= n; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

Some people may ask, why is another important feature of Dynamic Programming, “optimal substructure”, not covered? It will be covered below. The Fibonacci sequence example is not strictly Dynamic Programming, because it does not involve finding the maximum value. The above is intended to demonstrate the process of spiraling up algorithm design. Next, look at the second example, the change problem.

Change problem

Let’s take a look at the question first: Give you k kinds of coins with face value, the face value is c1, c2… ck, the number of each coin is unlimited, then give a total amount amount, and ask you how many coins you need at least to make up this amount, if it is impossible to make up, the algorithm returns -1. The function signature of the algorithm is as follows:

1
2
//coins is the optional coin face value, amount is the target amount
int coinChange(int[] coins, int amount);

For example, k = 3, the face value is 1, 2, and 5 respectively, and the total amount = 11. Then at least 3 coins are needed to make up, that is, 11 = 5 + 5 + 1.

How do you think computers should solve this problem? Obviously, it is to exhaust all possible methods of coin collection, and then find out how many coins are needed at least.

1 The recursion of violence

First of all, this problem is a Dynamic Programming problem because it has an “optimal substructure”. To meet the “optimal substructure”, the subproblems must be independent of each other. What does independence mean? You definitely don’t want to see a mathematical proof, I’ll use an intuitive example to explain.

For example, your original question is to get the highest total score, then your sub-question is to get the highest Chinese test and the highest math test… In order to get the highest score in each class, you have to get the highest score for the corresponding multiple-choice questions in each class, and the highest score for fill-in-the-blank questions… Of course, in the end, you will get full marks in each class, which is the highest total score.

The correct result is obtained: the highest total score is the total score. Because this process conforms to the optimal substructure, the sub-problems of “highest in each subject” are independent of each other and do not interfere with each other.

However, if you add a condition: your Chinese score and math score will restrict each other, and the other will increase. In this case, it is obvious that the highest total score you can get will not reach the total score, and you will get the wrong result according to the idea just now. Because the sub-problems are not independent, the Chinese and math scores cannot be optimal at the same time, so the optimal substructure is destroyed.

Back to the coin-making problem, why is it said to conform to the optimal substructure? For example, if you want to find the minimum number of coins when amount = 11 (the original problem), if you know the minimum number of coins (the sub-problem) to make up amount = 10, you only need to add one to the answer to the sub-problem (choose another coin with a face value of 1) is the answer to the original problem, because the number of coins is unlimited, and there is no reciprocity between sub-problems, they are independent of each other.

So, now that you know this is a Dynamic Programming problem, you need to think about how to list the correct state transition equations?

First, determine the “state”, which is the variable that changes in the original problem and sub-problems. Since the number of coins is unlimited, the only state is the target amount.

Then determine the definition of the dp function: the current target amount is n, and at least dp (n) coins are required to make up the amount.

Then determine the “choice” and select the best, that is, for each state, what choice can be made to change the current state. Specific to this problem, no matter what the target amount is, the choice is to select a coin from the denomination list coins, and the target amount will be reduced:

1
2
3
4
5
6
7
8
9
10
# Pseudo-code framework
def coinChange(coins: List[int], amount: int):
    Definition # : To make up an amount of n, at least dp (n) coins are required
    def dp(n):
        #  make a choice, choose the outcome that requires the least amount of coins
        for coin in coins:
            res = min (res, 1 + dp (n - corner))
        return res
    #  the question we are asking is dp (amount)
    return dp(amount)

Finally, clear the base case, obviously when the target amount is 0, the number of coins required is 0; when the target amount is less than 0, no solution, return -1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def coinChange(coins: List[int], amount: int):
    def dp(n):
        # base case
        if n  0: return 0
        if n < 0: return -1
        #  minimum, so initialize to positive infinity
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            #  unsolved sub-problem, skip
            if subproblem  -1: continue
            res = min(res, 1 + subproblem)

        return res if res != float('INF') else -1

    return dp(amount)

At this point, the state transition equation has actually been completed, the above algorithm is already a violent solution, and the mathematical form of the above code is the state transition equation:

dp(n) = 0, n = 0

dp(n) = -1, n < 0

dp(n) = min{dp(n - coin) + 1 | coin ∈ coins}, n > 0

At this point, this problem is actually solved, but we need to eliminate the overlapping sub-problem. For example, when amount = 11, coins = {1,2,5}, draw a recursion tree to see:

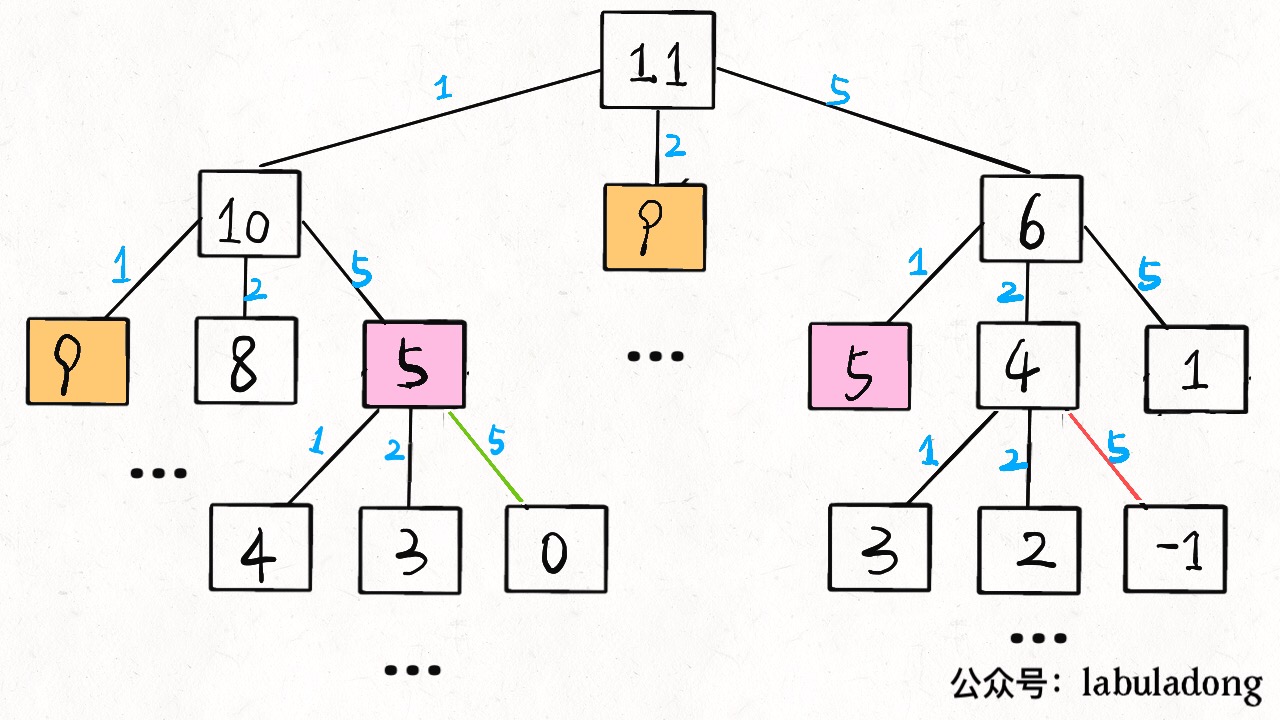
Time complexity analysis: total number of sub-problems x the time of each sub-problem.

The total number of subproblems is the number of recursion tree nodes, which is difficult to see. It is O (n ^ k), which is exponential in short. Each subproblem contains a for loop with complexity O (k). So the total time complexity is O (k * n ^ k), exponential.

  1. Recursion with memo

With just a few modifications, you can eliminate sub-problems through memos.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def coinChange(coins: List[int], amount: int):
    #  memo
    memo = dict()
    def dp(n):
        #  check memos to avoid double counting
        if n in memo: return memo[n]
        if n  0: return 0
            if n < 0: return -1
            res = float('INF')
            for coin in coins:
                subproblem = dp(n - coin)
                if subproblem  -1: continue
                res = min(res, 1 + subproblem)

            #  in the memo
            memo[n] = res if res != float('INF') else -1
            return memo[n]

	return dp(amount)

Without drawing the picture, it is obvious that the “memo” greatly reduces the number of sub-problems and completely eliminates the redundancy of sub-problems, so the total number of sub-problems will not exceed the number of amounts n, that is, the number of sub-problems is O (n). The time to process a sub-problem remains the same, still O (k), so the total time complexity is O (kn).

  1. Iterative solution of dp array

Of course, we can also use dp table from bottom to top to eliminate overlapping sub-problems. The definition of dp array is similar to that of dp function just now, and the definition is the same:

DP [i] = x means that at least x coins are needed when the target amount is i.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int coinChange(vector<int>& coins, int amount) {
    //The array size is amount + 1, and the initial value is also amount + 1.
    vector<int> dp(amount + 1, amount + 1);
    // base case
    dp[0] = 0;
    for (int i = 0; i < dp.size(); i++) {
        //the inner for is finding the minimum value of + 1 for all subproblems
        for (int coin : coins) {
            //The sub-problem is unsolved, skip it.
            if (i - coin < 0) continue;
            dp[i] = min(dp[i], 1 + dp[i - coin]);
        }
    }
    return (dp[amount]  amount + 1) ? -1 : dp[amount];
}

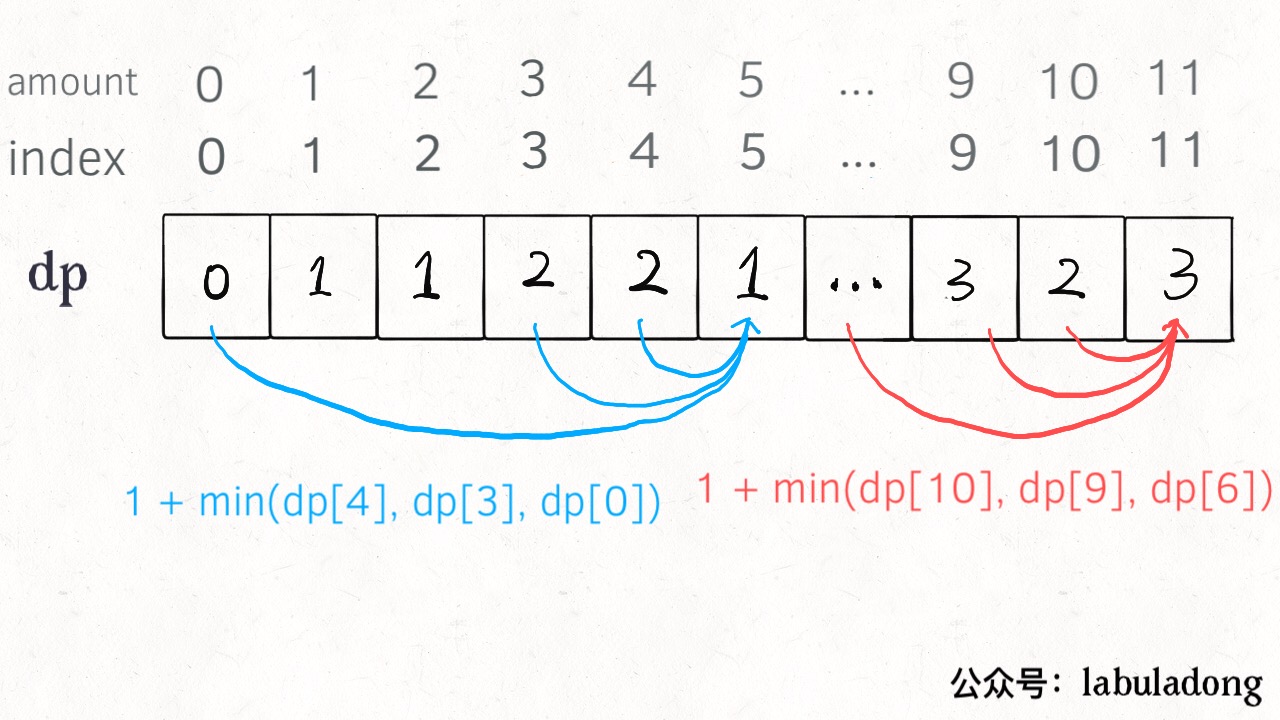
PS: Why is the dp array initialized to amount + 1, because the number of coins that make up the amount can only be equal to amount at most (all 1 yuan face value coins), so initializing to amount + 1 is equivalent to initializing to positive infinity, which is convenient for subsequent Take the minimum value.

Final summary

The first Fibonacci sequence problem explained how to optimize recursion trees using the “memo” or “dp table” method, and made it clear that these two methods are essentially the same, only top-down and bottom-up It’s just different.

The second change problem shows how to determine the “state transition equation” in a streamlined manner. As long as the violent recursion solution is written through the state transition equation, the rest is to optimize the recursion tree and eliminate overlapping sub-problems.

If you don’t know much about Dynamic Programming, you can still see it here. I really applaud you. I believe you have mastered the design skills of this algorithm.

In fact, there is no magic trick for computers to solve problems. Its only solution is to exhaust all possibilities. Algorithm design is nothing more than thinking about “how to exhaust” first, and then pursuing “how to exhaust intelligently”.

To list the dynamic transfer equations was to solve the problem of “how to exhaust”. The reason why it was difficult was because many exhaustions required recursion, and because some problems had complex solution spaces, it was not easy to exhaust them completely.

Memos and DP tables are pursuing “how to exhaust intelligently”. The idea of exchanging space for time is the only way to reduce the complexity of time. In addition, what else can you do?