string matching algorithm study notes

Posted on Edited on In Waline:

We usually work will often use SringA.indexOf (StringB) this substring lookup function, if we let ourselves implement, how will we achieve?

This time we record the four string matching algorithms we often say, namely BF, RK, BM and KMP algorithm.

The first two easy to think of, is also very simple, the latter two can understand the principle, these two algorithms are more difficult to understand the two, even if you understand it is difficult to write a bug-free program.

BF (brute force matching) algorithm

The BF in the BF algorithm is the abbreviation of Brute Force, which is called brute force matching algorithm in Chinese, also known as naive matching algorithm. As can be seen from the name, the string match type of this algorithm is very “violent”, of course, it will be relatively simple and easy to understand, but the corresponding performance is not high.

Before starting to explain this algorithm, I first define two concepts so that I can explain them later. They are primary strings and pattern strings. These two concepts are easy to understand. Let me give you an example and you will understand. For example, if we look for string B in string A, then string A is the primary string and string B is the pattern string. We denote the length of the primary string as n and the length of the pattern string as m. Because we are looking for the pattern string in the primary string, n > m.

As the simplest and most violent string matching algorithm, the idea of ** BF algorithm can be summarized in one sentence, that is, in the main string, we check the starting positions of 0, 1, 2… n-m and length m of n-m + 1 substring to see if there is a ** that matches the pattern string.

For example:

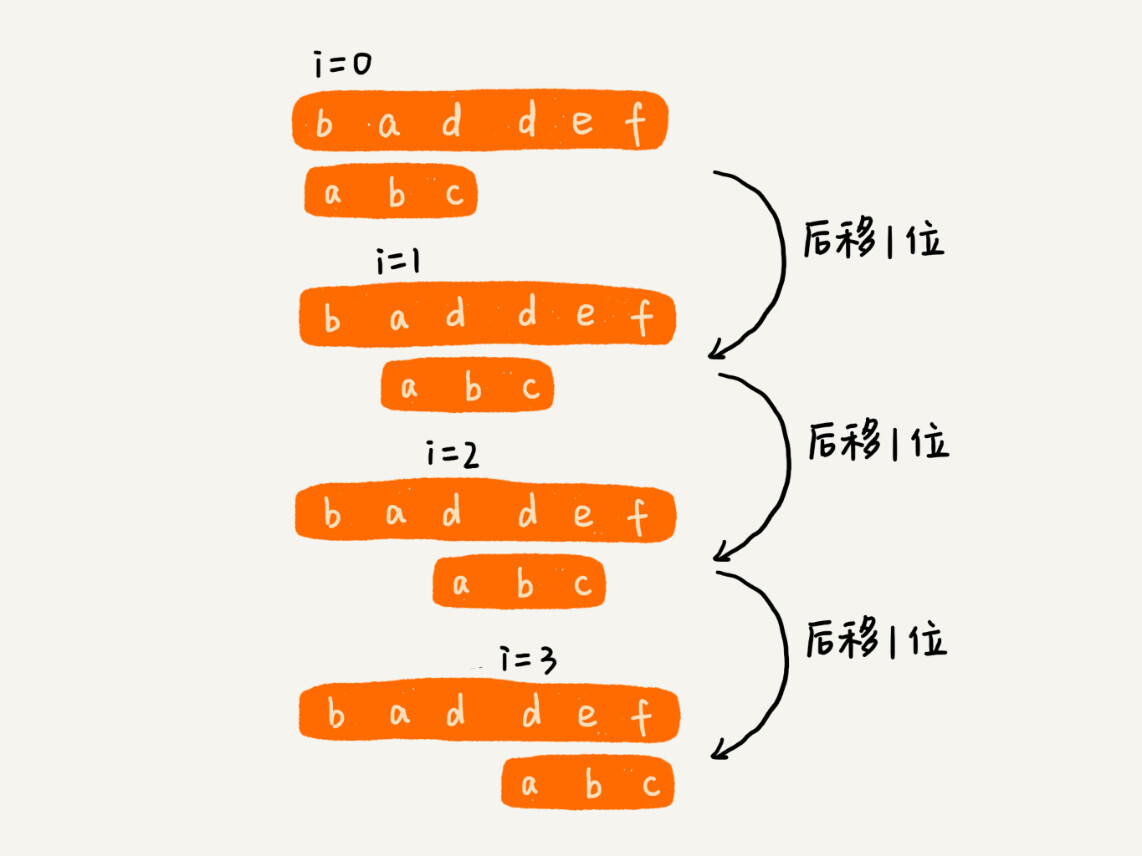
From the above algorithm ideas and examples, we can see that in extreme cases, such as the main string is “aaaaa… aaaaaa” (the ellipsis indicates that there are many repeating characters a), and the pattern string is “aaaaab”. We compare m characters each time, and compare n -m + 1 times, so the worst-case time complexity of this algorithm is O (n * m).

Although in theory, the time complexity of the BF algorithm is very high, O (n * m), in actual development, it is a more commonly used string matching algorithm.

Why do you say that? There are two reasons. First, in actual software development, in most cases, the length of the pattern string and the main string is not too long. And every time the pattern string matches a substring in the main string, when it encounters a character that cannot be matched halfway, it can stop, and there is no need to compare all m characters. So, although the theoretical worst-case time complexity is O (n * m), statistically speaking, in most cases, the algorithm execution efficiency is much higher than this.

Therefore, although this algorithm has a high time complexity, if our data is not complicated, we can use this algorithm, because this algorithm is simple and not easy to make mistakes.

RK algorithm

The full name of the RK algorithm is Rabin-Karp algorithm, named after its two inventors, Rabin and Karp. This algorithm is not difficult to understand. Personally, I think it is actually an upgraded version of the BF algorithm just mentioned.

When I talk about the BF algorithm, I said that if the pattern string length is m and the main string length is n, then in the main string, there will be n-m + 1 substrings of length m. We only need to violently compare This n-m + 1 substring and the pattern string can find the substring that matches the main string and the pattern string.

However, every time you check whether the main string matches the substring, you need to compare each character in turn, so the time complexity of the BF algorithm is relatively high, which is O (n * m). We make a slight modification to the naive string matching algorithm and introduce the hash algorithm, and the time complexity will be reduced immediately.

The idea of the RK algorithm is as follows: ** We use the hash algorithm to find the hash value of the n-m + 1 substrings in the main string, and then compare the size with the hash value of the pattern string one by one. If the hash value of a substring is equal to the pattern string, it means that the corresponding substring matches the pattern string ** (we will talk about the hash collision problem here, we will talk about it later). Because the hash value is a number, the comparison between numbers is very fast, so the efficiency of comparing pattern strings and substrings is improved.

How to cleverly design hash functions

When calculating the hash value of a substring through a hash algorithm, we need to traverse each character in the substring. Although the efficiency of comparing pattern strings with substrings has improved, the overall efficiency of the algorithm has not improved. Is there a way to improve the efficiency of the hash algorithm in calculating the hash value of a substring?

Here we will use a more common but also more practical idea, ** If your results can be calculated by the previous calculation results, it can greatly simplify the calculation, such as our recursive formula in Dynamic Programming, prefix and so on are used in this idea. **

Since we calculate the hash value of the substring in turn when the previous and the next substring have a large overlap, if our hash function can use the calculation results of these overlapping parts, we can avoid a lot of repeated calculations.

For example

Assuming that the string contains only 26 lowercase characters a~ z, we use two hexadecimals to represent a string, and the corresponding hash value is the result of converting the two hexadecimals into decimal. This hash algorithm has a feature. In the main string, the calculation formula of the hash value of two adjacent substrings has a certain relationship.

Improved hash function

  • If you still want to improve efficiency, you can spend further time, that is, the calculation of 26 ^ (m-1), we can improve efficiency by looking up the table. We calculate 26 ^ 0, 26 ^ 1, 26 ^ 2 in advance… 26 ^ (m-1), and store it in an array of length m, and the “power” in the formula corresponds to the index of the array. When we need to calculate 26 to the power of x, we can take the value from the position where the index of the array is x and use it directly, saving the calculation time.
  • Of course, the above hash function does not have hash conflicts, but it takes up a lot of space, and may even exceed the storage limit of digital variables. In this case, we can sacrifice some performance and use a simple hash algorithm, such as simple ascii code addition. If the hash value is the same when comparing, we will compare it again. This idea is very similar to Bloom filter.

BMS algorithm

Core ideas

The matching process between a pattern string and a main string is seen as the pattern string sliding back and forth in the main string. When encountering a mismatched character, the BF algorithm and the RK algorithm do it by sliding the pattern string back one bit, and then re-matching from the first character of the pattern string.

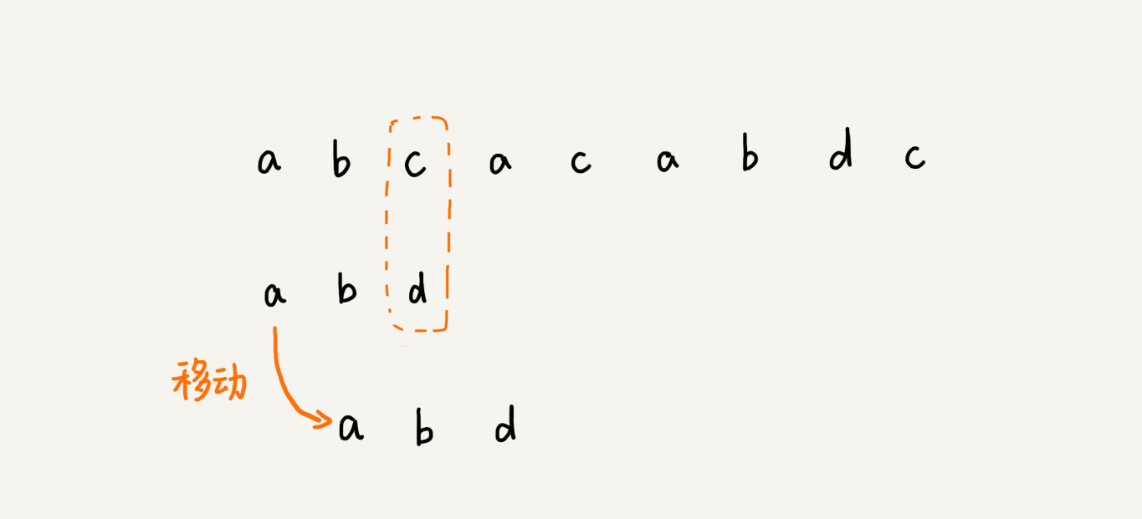
4316dd98eac500a01a0fd632bb5e77f9

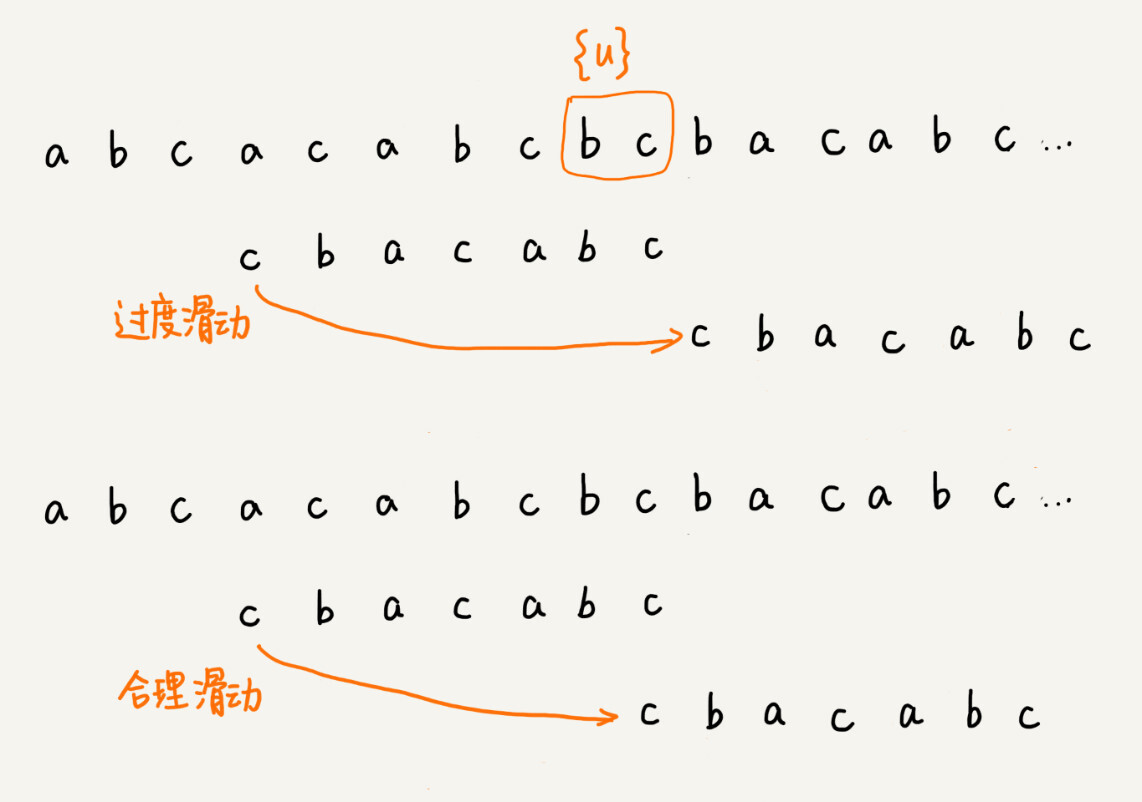
In this example, the c in the main string does not exist in the pattern string, so when the pattern string slides back, as long as c overlaps with the pattern string, it will definitely not match. Therefore, we can slide the pattern string back a few more times at a time to move the pattern string to the back of c.

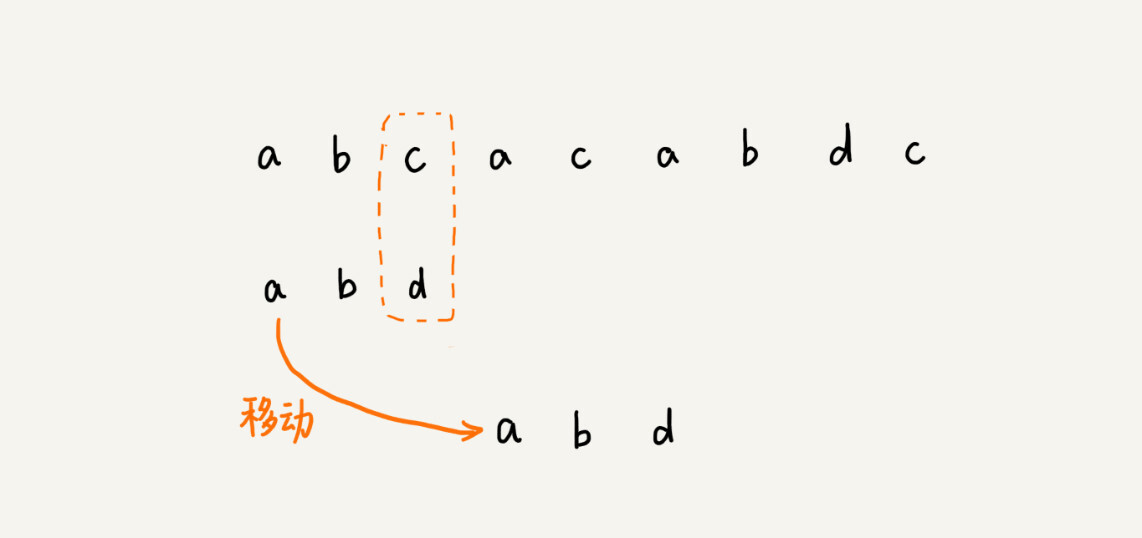
cf362f9e59c01aaf40a34d2f10e1ef15

By the phenomenon to find the law, you can think about it, ** when you encounter mismatched characters, what are the fixed rules, you can slide the pattern string back a few more times **? In this way, sliding back several times at once, wouldn’t the matching efficiency be improved? The BM algorithm we are going to talk about today is essentially looking for this law. With the help of this law, in the process of matching the pattern string with the main string, when a character of the pattern string and the main string does not match, it is possible to skip some cases that will definitely not match and slide the pattern string back a few more times.

Principle analysis

The BM algorithm consists of two parts, namely the bad character rule and the good suffix shift. Let’s see how these two rules work in turn.

Bad character rule

For the first two algorithms, in the process of matching, we match the characters in the main string in descending order according to the subscript of the pattern string. This matching order is more in line with our habits of thinking, while the matching order of the BM algorithm is more special. It matches backwards in descending order according to the subscript of the pattern string. I drew a picture, you can take a look.

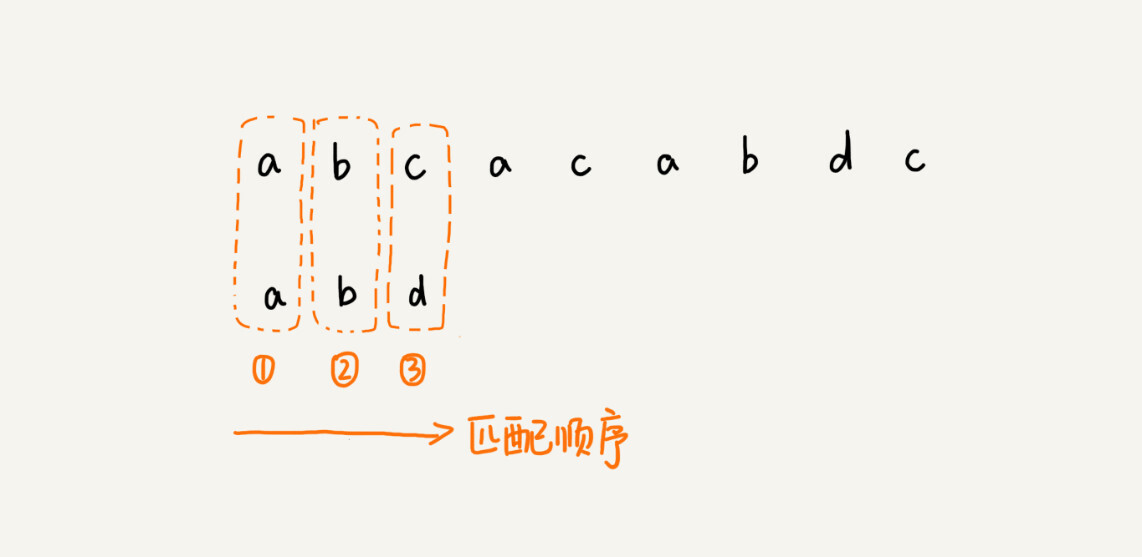
29521f541dd45e13162013b3364fece1

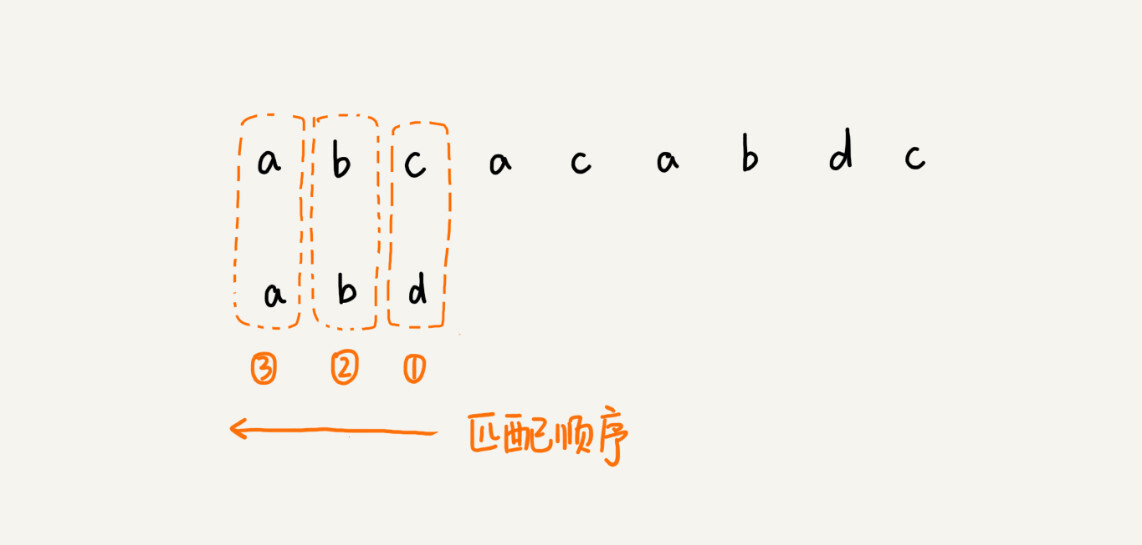
540809418354024206d9989cb6cdd89e

Here’s a question, why do we need to look from back to front here?

We match backwards from the end of the pattern string, when we find that a character cannot be matched. We call this unmatched character a bad character (a character in the main string).

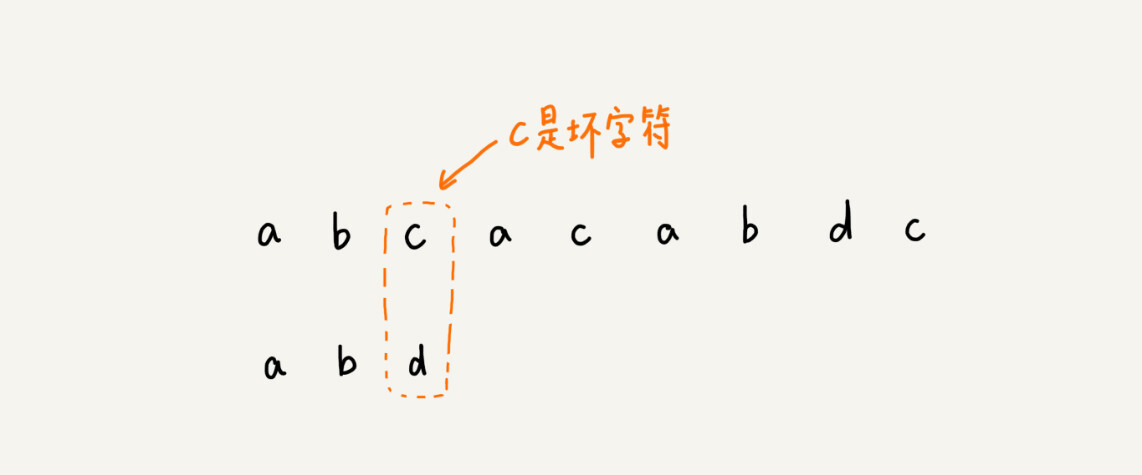
We take the bad character c to look up in the pattern string and find that the character does not exist in the pattern string, that is, the character c cannot match any character in the pattern string. At this time, we can slide the pattern string directly back three places, slide the pattern string to the position after c, and start the comparison from the end character of the pattern string.

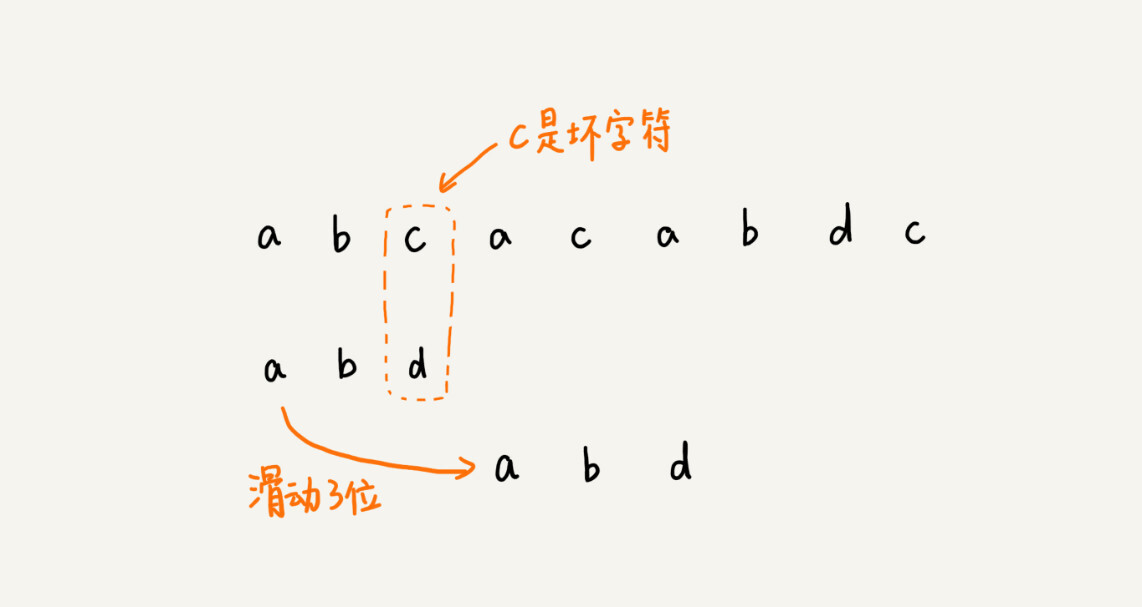
At this time, we found that the last character d in the pattern string still cannot match the a in the main string. At this time, can we slide the pattern string back three places? The answer is no. Because at this time, the bad character a exists in the pattern string, and the position where the subscript is 0 in the pattern string is also the character a. In this case, we can slide the pattern string back two bits to align the two a’s up and down, and then start from the end character of the pattern string to match again.

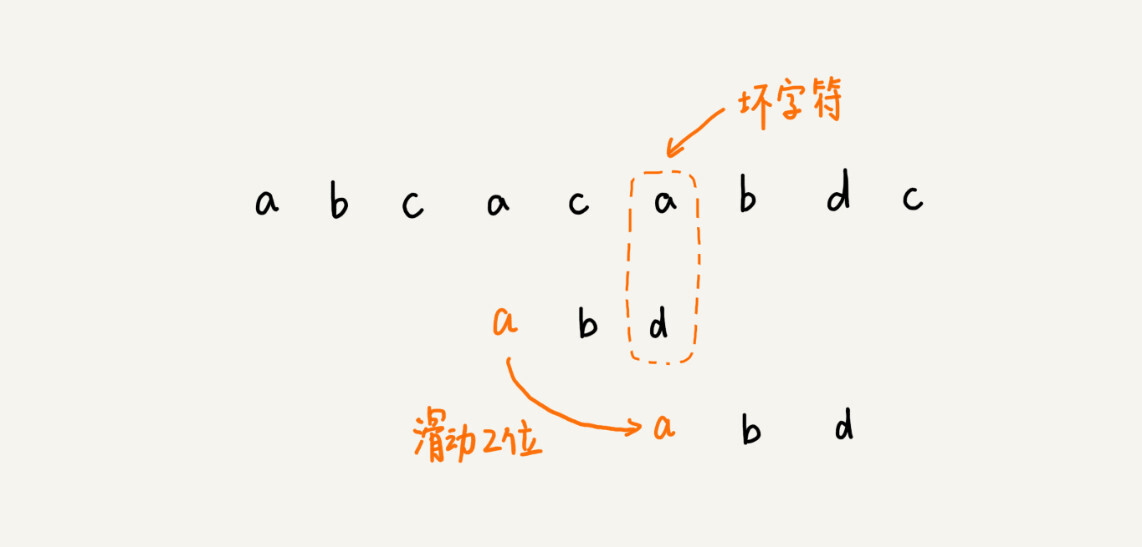
When the first does not match, we slide three, the second time does not match, we will move the pattern string back two bits, the specific sliding number, in the end there is no law?

When a mismatch occurs, we denote the subscript of the character in the pattern string corresponding to the bad character as si. If the bad character exists in the pattern string, we denote the subscript of the bad character in the pattern string as xi. If it does not exist, we denote xi as -1. Then the number of digits moved back by the pattern string is equal to si-xi. (Note that the subscripts I’m talking about here are all subscripts of characters in the pattern string).

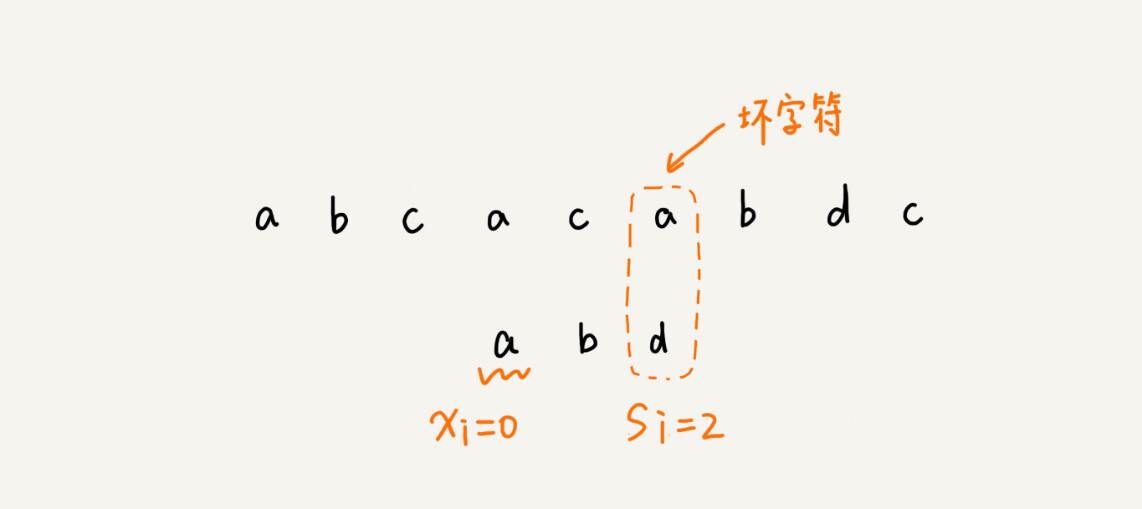
Here I want to make a special point. If bad characters appear in multiple places in the pattern string, then when we calculate xi, we choose the last one, because this will not let the pattern string slide too much, resulting in the situation that could have been matched. Slide over.

Using the bad character rule, the BM algorithm has a very low time complexity of O (n/m) in the best case. For example, the main string is aaabaaabaaaabaaabaaab, and the pattern string is aaaa. Each comparison, the pattern string can be directly shifted back four bits, so the BM algorithm is very efficient when matching pattern strings and main strings with similar characteristics.

However, simply using the bad character rule is not enough. Because the shift bits calculated according to si-xi may be negative numbers, such as the main string is aaaaaaaaaaaaaaaaaaaa, and the pattern string is baaa. Not only will the pattern string not slide backwards, but it may also go backwards. Therefore, the BM algorithm also needs to use the “good suffix rule”.

So far, in fact, as long as we limit the calculated number of moving bits to be negative, the BM algorithm can work properly.

Good suffix rule

The good suffix rule is actually very similar to the idea of the bad character rule. Take a look at the picture below. When the pattern string slides to the position in the picture, 2 characters of the pattern string and the main string match, and the penultimate character does not match.

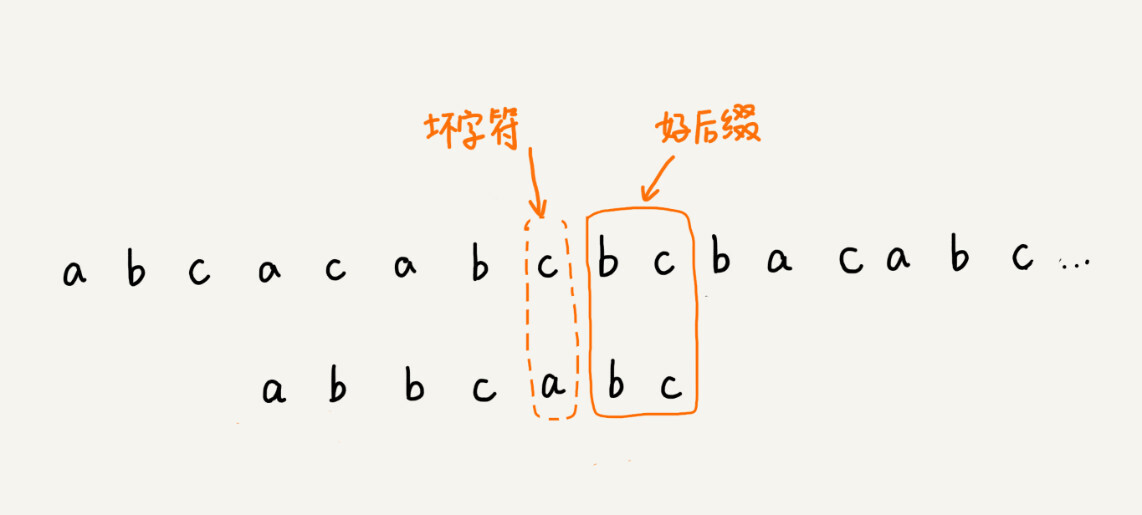
How to slide the pattern string at this time? Of course, we can also use the bad character rule to calculate the number of sliding bits of the pattern string, but we can also use the good suffix handling rule. How to choose between the two rules, I will talk about it later. Leaving this question aside, now let’s see, how does the good suffix rule work?

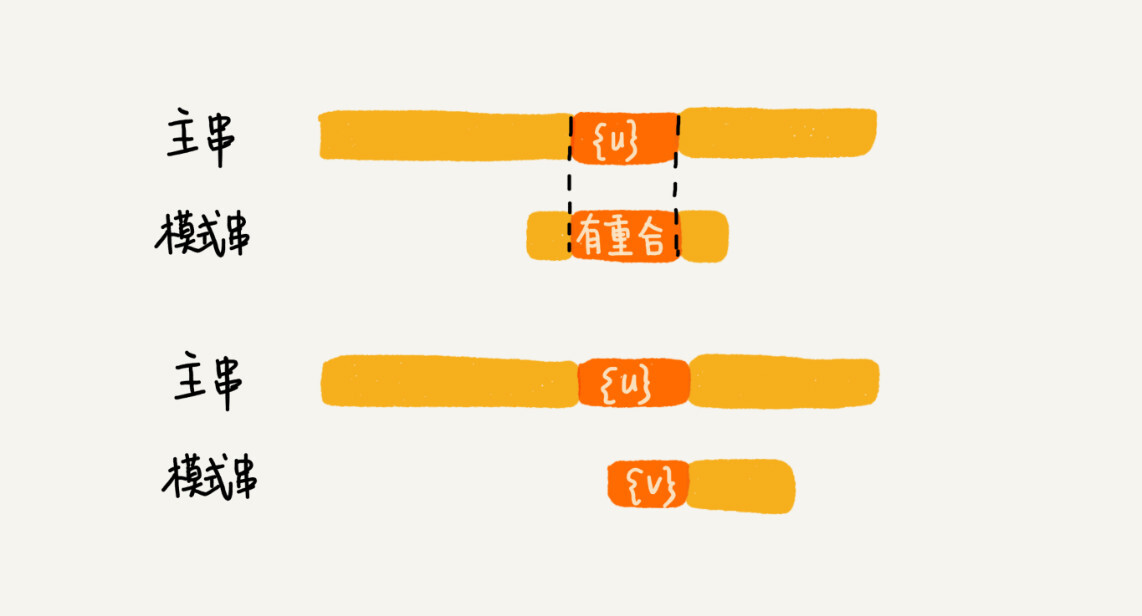
We call the matched bc a good suffix, denoted {u}. We take it and look it up in the pattern string. If we find another substring {u *} that matches {u}, then we slide the pattern string to the place where the substring {u *} aligns with the main string {u}.

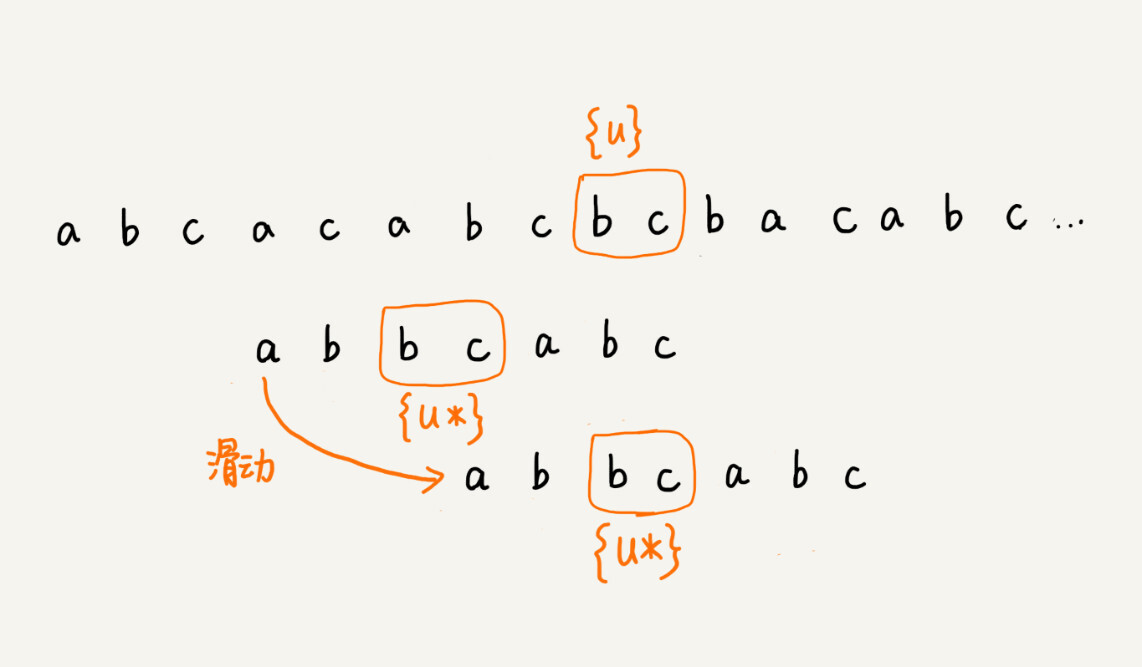
If we can’t find another substring equal to {u} in the pattern string, we slide the pattern string directly to the back of {u} in the main string, because any previous sliding back does not match the main string. In the case of {u}.

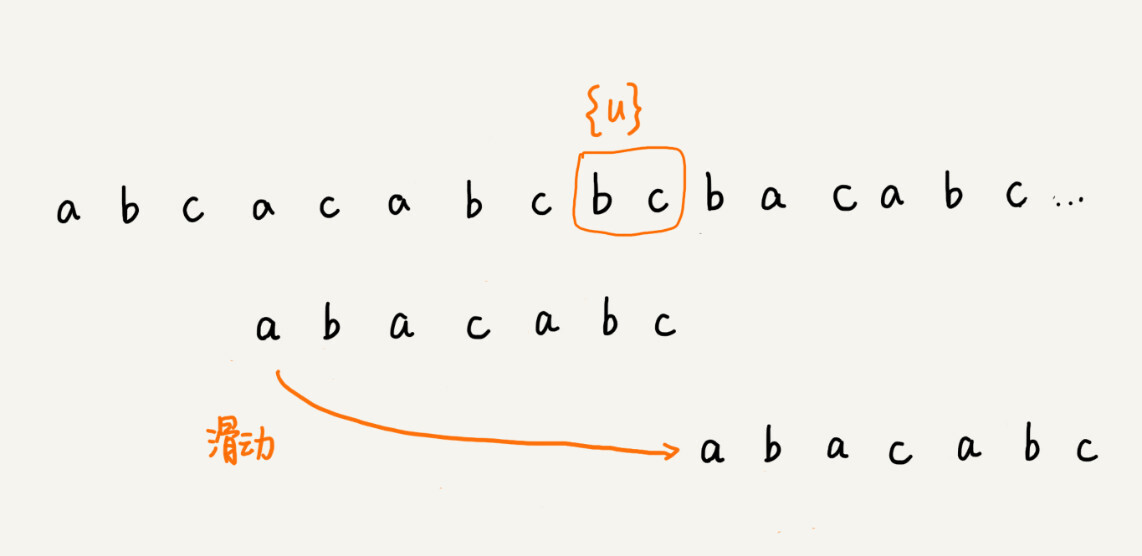
However, when there is no substring equal to {u} in the pattern string, we slide the pattern string directly after the main string {u}. Is this a bit too much? Let’s take a look at the following example. Here bc is a good suffix, although there is no other matching substring {u *} in the pattern string, if we move the pattern string after the good suffix, as shown in the figure, we will miss the situation where the pattern string and the main string can match.

If the good suffix does not have a matching substring in the pattern string, then in the process of sliding the pattern string back step by step, as long as {u} in the main string overlaps with the pattern string, it will definitely not be a perfect match. But when the pattern string slides to the point where the prefix partially overlaps with the suffix of {u} in the main string, and the overlapping parts are equal, there may be an exact match.

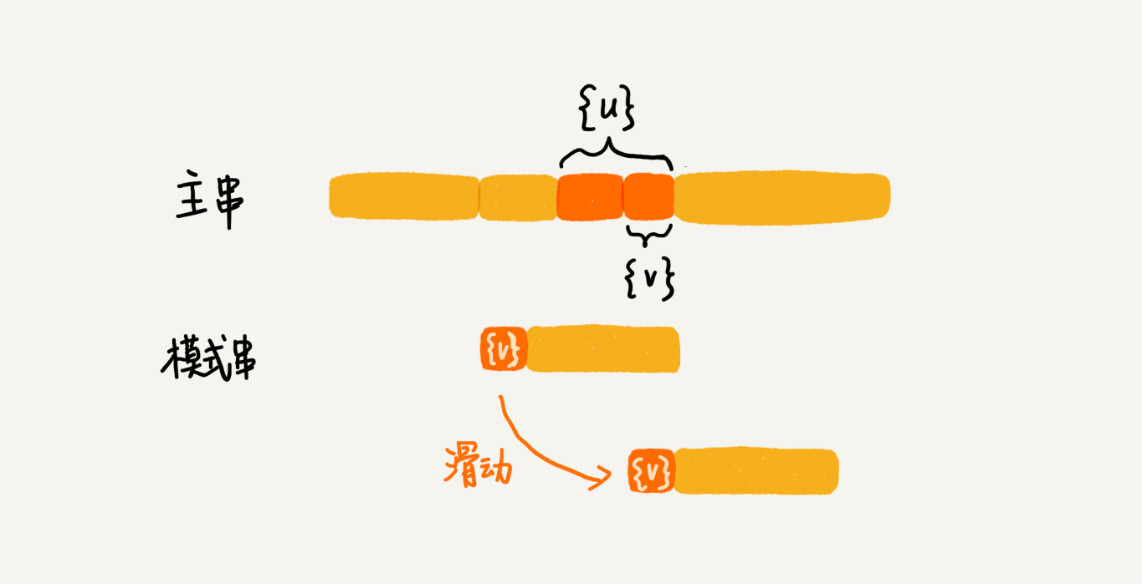
Therefore, in view of this situation, we should not only look at the suffix in the pattern string, whether there is another matching substring, but also examine the suffix substring of the suffix, whether there is a match with the prefix substring of the pattern string.

The so-called suffix substring of a string s is the substring whose last character is aligned with s. For example, the suffix substring of abc includes c and bc. The so-called prefix substring is the substring whose starting character is aligned with s. For example, the prefix substring of abc has a, ab. From the suffix substrings of good suffixes, we find the longest one that matches the prefix substring of the pattern string, assuming it is {v}, and then slide the pattern string to the position shown in the figure.

The basic principles of bad characters and good suffixes have been covered. When a pattern string does not match a character in the main string, how to choose whether to use the good suffix rule or the bad character rule to calculate the number of bits that the pattern string slides back? We can calculate the number of bits that the good suffix and the bad character slide back separately, and then take the largest of the two numbers as the number of bits that the pattern string slides back. This approach also avoids the situation we mentioned earlier, where the number of bits slid back calculated according to the bad character rule may be negative.

Algorithm implementation

Bad character

The “bad character rule” itself is not difficult to understand. When encountering a bad character, we need to calculate the number of digits moved back si-xi, of which the calculation of xi is the key. How do we find xi? Or, how to find the position of the bad character in the pattern string?

If we take bad characters and traverse the search sequence in the pattern string, it will be inefficient and will inevitably affect the performance of this algorithm. Is there a more efficient way? The hash table we learned before can come in handy here. We can save each character in the pattern string and its subscript to the hash table. This way you can quickly find the subscript of the bad character in the pattern string.

Regarding this hash table, we only implement the simplest case. Assuming that the character set of the string is not very large and the length of each character is 1 byte, we use an array of size 256 to record the position of each character in the pattern string.

The index of the array corresponds to the ASCII code value of the character, and the array stores the position where the character appears in the pattern string. If the above process is translated into code, it looks like the following. Where the variable b is the pattern string, m is the length of the pattern string, and bc represents the hash table just mentioned.

1
2
3
4
5
6
7
8
9
10
11

Private static final int SIZE = 256;//global or member variables
private void generateBC(char[] b, int m, int[] bc) {
  for (int i = 0; i < SIZE; ++i) {
    Bc [i] = -1;//initialize bc
  }
  for (int i = 0; i < m; ++i) {
    Int ascii = (int) b [i];//calculate the ASCII value of b [i]
    bc[ascii] = i;
  }
}

After mastering the bad character rules, we first write the large framework of the BM algorithm code. First, we do not consider the good suffix rules, only use the bad character rules, and do not consider the negative number of moving bits calculated by si-xi.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

public int bm(char[] a, int n, char[] b, int m) {
  Int [] bc = new int [SIZE];//Record the last occurrence of each character in the pattern string
  GenerateBC (b, m, bc);//build bad character hash table
  Int i = 0;//i indicates the first character of the main string aligned with the pattern string
  while (i <= n - m) {
    int j;
    For (j = m - 1; j > = 0; --j ) { // pattern string matches backwards
      If (a [i + j]! = b [j]) break;//The subscript in the pattern string corresponding to the bad character is j
    }
    if (j < 0) {
      Return i;//The match is successful, return the position of the first matching character of the main string and the pattern string
    }
    //This is equivalent to sliding the pattern string back j-bc [ (int) a [i + j]] bit
    i = i + (j - bc[(int)a[i+j]]); 
  }
  return -1;
}

Good suffix

Let’s briefly review the core content of the rules for handling suffixes mentioned earlier:

  • In the pattern string, find another substring that matches the good suffix;

  • In the suffix substring of a good suffix, find the longest suffix substring that matches the pattern string prefix substring;

Without considering efficiency, both operations can be solved with a very “violent” match search method. However, if you want the BM algorithm to be very efficient, this part cannot be too inefficient. How to do it?

** Because a good suffix is also a suffix substring of the pattern string itself, we can pre-calculate each suffix substring of the pattern string by pre-processing the pattern string ** before the pattern string and the main string are officially matched. The position of another matching substring.

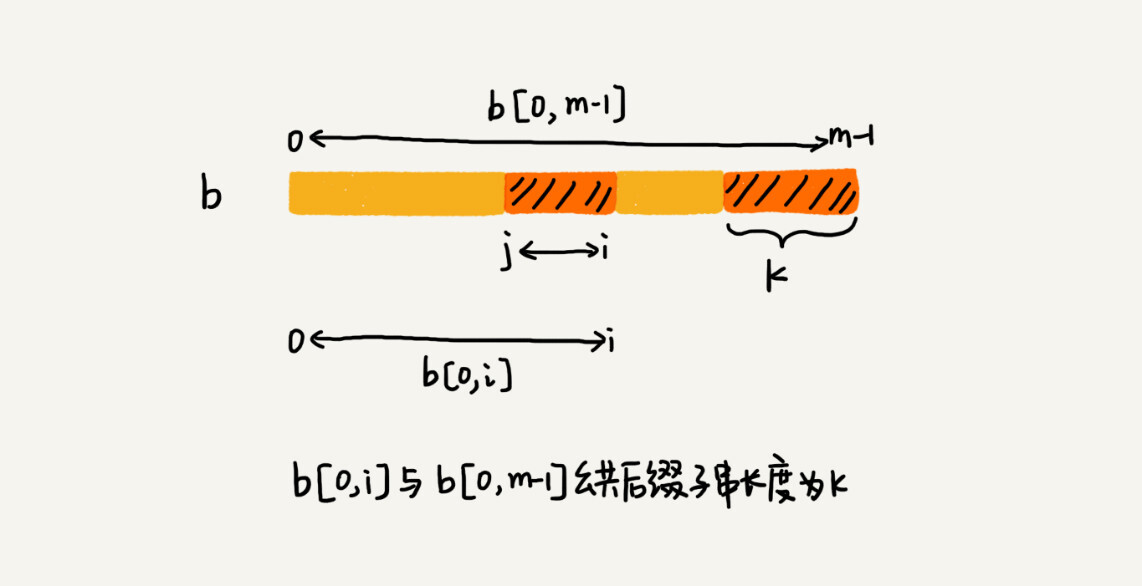
How to represent different suffix substrings in a pattern string? Because the position of the last character of the suffix substring is fixed and the subscript is m-1, we only need to record the length. By length, we can determine a unique suffix substring.

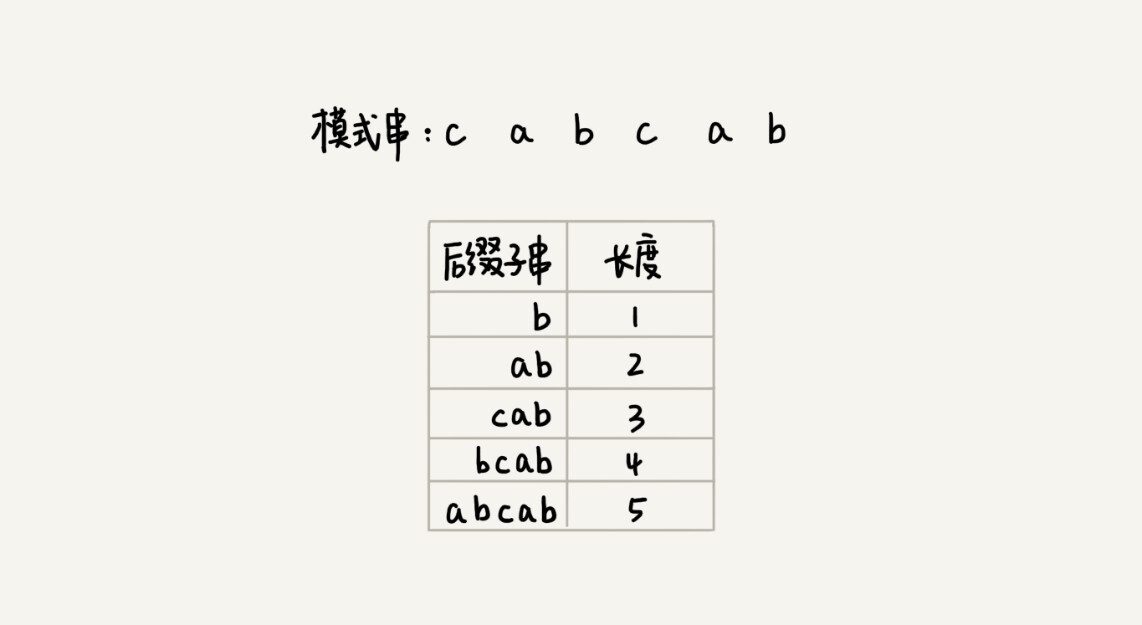
Now, we are going to introduce the most critical variable, the suffix array. The subscript k of the suffix array represents the length of the suffix substring. The array value corresponding to the subscript stores the starting subscript value of the substring {u *} that matches the suffix {u} in the pattern string.

If there are multiple (more than one) substrings in the pattern string that match the suffix substring {u}, which substring’s starting position should be stored in the suffix array? In order to avoid sliding the pattern string too far back, we must store the starting position of the last substring in the pattern string, that is, the starting position of the substring with the largest subscript. However, is this processing enough?

In fact, it’s not enough to just choose the last substring fragment to store. Let’s recall the good suffix rule again. We not only have to find another substring in the pattern string that matches the good suffix, but also find the longest suffix substring in the suffix substring of the good suffix that matches the prefix substring of the pattern string.

If we only record the suffix we just defined, we can actually only process the first half of the rule, that is, in the pattern string, find another substring that matches the good suffix. So, in addition to the suffix array, we also need another prefix array of type boolean to record whether the suffix substring of the pattern string matches the prefix substring of the pattern string

Now, let’s take a look, how to calculate and fill the values of these two arrays?

This calculation process is very clever. We take the substring labeled from 0 to i (i can be 0 to m-2) and the entire pattern string, and find the common suffix substring. If the length of the common suffix substring is k, then we record suffix [k] = j (j represents the starting subscript of the common suffix substring). If j is equal to 0, that is, the common suffix substring is also a prefix substring of the pattern string, we record prefix [k] = true.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

//b represents the pattern string, m represents the length, suffix, prefix array is applied in advance
private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
  for (int i = 0; i < m; ++i) { // 初始化
    suffix[i] = -1;
    prefix[i] = false;
  }
  for (int i = 0; i < m - 1; ++i) { // b[0, i]
    int j = i;
    Int k = 0;//length of common suffix substring
    while (j >= 0 && b[j]  b[m-1-k]) { // 与b[0, m-1]求公共后缀子串
      --j;
      ++k;
      Suffix [k] = j + 1;//j + 1 indicates the starting subscript of the common suffix substring in b [0, i]
    }
    if (j  -1) prefix[k] = true; //如果公共后缀子串也是模式串的前缀子串
  }
}

With these two arrays, we now see, in the pattern string with the main string matching process, encountered can not match the character, according to a good suffix rules, how to calculate the number of bits of sliding pattern string back?

Suppose the length of the good suffix is k. We first take the suffix and look for its matching substring in the suffix array. If suffix [k] is not equal to -1 (-1 means no matching substring exists), then we move the pattern string back j-suffix [k] + 1 bits (j means the character subscript in the pattern string corresponding to the bad character). If suffix [k] is equal to -1, it means that there is no other substring segment in the pattern string that matches the good suffix. We can use the following rule to handle

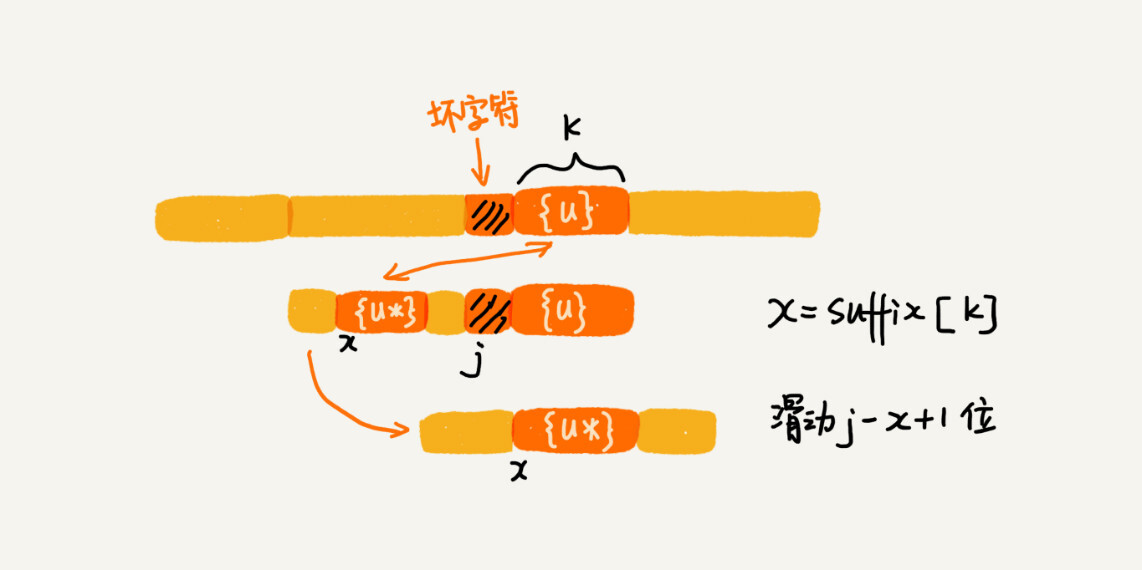
The length k of the suffix substring b [r, m-1] of a good suffix (where r takes the value from j + 2 to m-1) = m-r. If prefix [k] is equal to true, it means that the suffix of length k substring has a matching prefix substring, so we can shift the pattern string back r bits.

If neither rule finds a substring that matches the suffix and its suffix substring, we shift the entire pattern string back m bits.

Complete code

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

//a, b represents the main string and the pattern string; n, m represents the length of the main string and the pattern string.
public int bm(char[] a, int n, char[] b, int m) {
  Int [] bc = new int [SIZE];//Record the last occurrence of each character in the pattern string
  GenerateBC (b, m, bc);//build bad character hash table
  int[] suffix = new int[m];
  boolean[] prefix = new boolean[m];
  generateGS(b, m, suffix, prefix);
  Int i = 0;//j indicates the first character matched by the main string and the pattern string
  while (i <= n - m) {
    int j;
    For (j = m - 1; j > = 0; --j ) { // pattern string matches backwards
      If (a [i + j]! = b [j]) break;//The subscript in the pattern string corresponding to the bad character is j
    }
    if (j < 0) {
      Return i;//The match is successful, return the position of the first matching character of the main string and the pattern string
    }
    int x = j - bc[(int)a[i+j]];
    int y = 0;
    If (j < m-1 ) { // if there is a good suffix
      y = moveByGS(j, m, suffix, prefix);
    }
    i = i + Math.max(x, y);
  }
  return -1;
}

//j represents the subscript of the character in the pattern string corresponding to the bad character; m represents the length of the pattern string
private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {
  Int k = m - 1 - j;//good suffix length
  if (suffix[k] != -1) return j - suffix[k] +1;
  for (int r = j+2; r <= m-1; ++r) {
    if (prefix[m-r]  true) {
      return r;
    }
  }
  return m;
}
JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
const SIZE = 256;
const generateBC = (b) => {
    let n = b.length;
    let bc = new Array(SIZE).fill(-1);
    for(let i = 0; i < n; i++) {
        let ascii = b[i].charCodeAt();
        bc[ascii] = i;
    }
    return bc;
}

const generateGS = (b) => {
    let m = b.length;
    let suffix = new Array(m).fill(-1);
    let prefix = new Array(m).fill(false);
    for(let i = 0; i < m - 1; i++) {
        let j = i, k = 0;
        while(j >= 0 && b[j]  b[m - 1 - k]) {
            suffix[++k] = j--;
        }
        if (j = -1) {
            prefix[k] = true;
        }
    }
    return {
        suffix,
        prefix
    };
}

const moveByGS = (j, suffix, prefix) => {
    const m = suffix.length;
    let k = m - j - 1;
    if (suffix[k] != -1) {
        return j - suffix[k] + 1;
    }
    for(let r = j + 2; r < m; r++) {
        if (prefix[m - r]) {
            return r;
        }
    }
    return m;
}

const bm = (a, b) => {
    const bc = generateBC(b);
    const { suffix, prefix } = generateGS(b);
    let i = 0, n = a.length, m = b.length;
    while(i < n - m) {
        let j = 0;
        for (j = m - 1; j >= 0; --j) {
            if (a[i + j] != b[j]) {
                break;
            }
        }
        if (j < 0) {
            return i;
        }
        let x = j - bc[a[i + j].charCodeAt()];
        let y = 0;
        if (j < m - 1) {
            y = moveByGS(j, suffix, prefix);
        }
        i += Math.max(x, y);
    }
    return -1;
}

KMP

https://sunra.top/posts/cd079caf/

Note:

The pictures in this article are all from Geek Time “The beauty of data structures and algorithms”