数学之美梳理(九)马尔科夫链的扩展——贝叶斯网络
之前我们讲过马尔科夫链,它描述了一种状态序列,其每个状态值取决于前面有限个状态。对很多实际问题,这种模型是一种很粗略的简化。在现实生活中,很多事物的相互关联并不能用一条链来串起来,很可能是交叉的。
贝叶斯网络
如图所示,心血管疾病和成因之间的关系错综复杂,显然无法用一条链来表示:
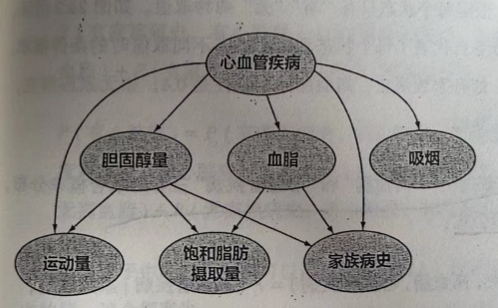
这个有向图可以看作是一个网络,其中每个圆圈表示一个状态,状态之间的连线表示他们的因果关系,比如从心血管疾病出发到吸烟的弧线表示心血管疾病可能与吸烟有关。‘
假设在这个图中,马尔科夫假设成立,即每个状态只跟与他直接相连的状态有关,而跟与它间接相连的状态无关,那么它就是贝叶斯网络。
不过要注意,这两个状态A和B之间没有直接的有向弧链接,只说明他们之间没有直接的因果关系,但这并不表示状态A不会通过其他状态间接影响状态B,只要在图中有一条从A到B的路径,这两个状态就还是有间接的相关性。
所有这些关系,都可以有一个量化的可信度,即用一个概率描述。也就是说,贝叶斯网络上的弧上可以有附加的权重。
马尔可夫假设保证了贝叶斯网络便于计算。
在网络中,每个节点的概率,都可以用贝叶斯公式来计算,贝叶斯网络因此而得名。由于每个弧都有一个可信度,贝叶斯网络也被称作信念网络。
对上面的例子,我们做一个简化,假设只有三个状态,“心血管疾病”,“高血脂”和“家族病史”。用这个简化的例子来说明这个网络中的一些概率是如何通过贝叶斯公式计算出来的。为了简单起见,假定每个状态只有“有”“无”两种取值。
如图所示,图中的三个部分分别表示每个状态和组合状态不同取值时的条件概率,表中数字说明,如有家族病史,高血脂的可能性是0.4,如无家族病史,这个可能性只有0.1。
如果要计算“心血管疾病”,“高血脂”和“家族病史”的联合概率分布,可以利用贝叶斯公式。
只要代入表中的数值就可以计算出概率。
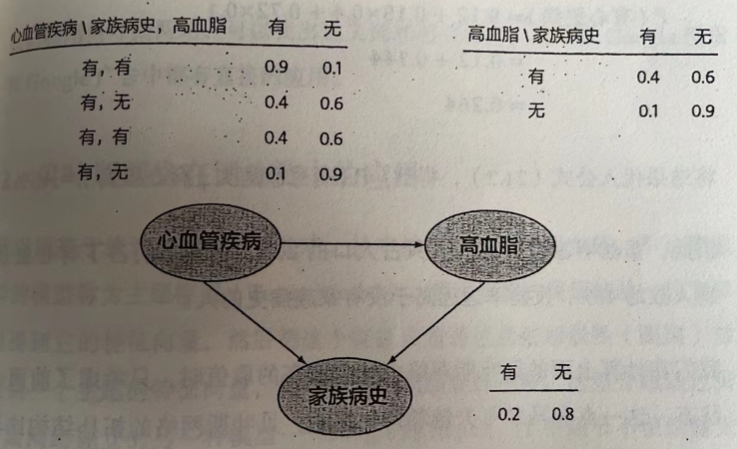
再比如,如果问心血管疾病有多大的可能是由家族病史引起的,也可以通过整个贝叶斯网络计算出来:
其中:
这两个式子中的每一项都可以通过公式1计算出,带入表中的数据,整个值的概率为。
我们在计算上面贝叶斯网络中每个状态的取值时,只考虑了前面一个的状态,这一点和马尔可夫链相同。但是贝叶斯网络的拓扑结构比马尔可夫链更加灵活,它不受马尔科夫链的链状结构的约束,因此可以更精确地描述事件之间地关联性。可以讲,马尔科夫链是贝叶斯网络的特例,而贝叶斯网络是马尔可夫链的推广。
使用贝叶斯网络必须先确认这个网络的拓扑结构,还要知道各个状态之间相关的概率,得到这些参数的过程分别叫结构训练和参数训练,统称训练。和训练马尔可夫模型一样,训练贝叶斯网络要用到一些已知数据。比如训练上面的网络,需要知道一些心血管疾病和吸烟,家族病史等情况。相比马尔科夫链,贝叶斯网络的训练更加复杂,从理论上讲,它是一个NP完全问题,也就是说,对于现在的计算机是不可解的。但是对于某些应用,这个训练过程可以简化,并在计算机上实现。
贝叶斯网络在图像处理,文字处理,支持决策方面有很多应用,在文字处理方面,语义相近的词之间的关系可以用贝叶斯网络来表示。
贝叶斯网络的训练
使用贝叶斯网络首先要确定它的结构。对于简单问题,比如心血管疾病的例子,直接由专家给出结构即可,但是,稍微复杂一点的问题,已经无法人工给出结构了,需要通过机器学习得到。
优化的贝叶斯网络要保证它产生的序列(比如“家族病史”->“高血脂”->“心血管疾病”就是一个序列)从头到尾的可能性最大,如果是使用概率做度量,就是后验概率最大。
当然,产生一个序列可以有多条路径,从理论上讲,需要完备的穷举搜索,即考虑到每一条路径,才能得到全局最优,但这样的计算复杂度是NP困难的,因此一般采用贪心算法,也就是在每一步时,沿着箭头的方向寻找有限步。当然这样会导致陷入局部最优,并且最终远离全局最优。一个防止陷入局部最优的方法,就是采用蒙特卡洛方法,用许多随机数在贝叶斯网络中试一试,看看是否陷入了局部最优。这个方法计算量比较大,最近最新的方法是利用信息论,计算节点之间两两的互信息,只保留互信息较大的节点直接的链接,然后再对简化的网络进行完备的搜索,找到全局最优的结构。
确定贝叶斯网络的结构后,就要确定这些节点之间的弧的权重了。假定这些权重用条件概率来度量,为此,需要一些训练数据,我们只需要最优化贝叶斯网络的参数,使得观察到的这些数据的概率(即后验概率)达到最大。这个过程就是期望最大化过程。
在计算后验概率时,计算的是条件X和条件Y结果之间的联合概率P(X|Y)。我们的训练数据会提供一些P(X|Y)的限制条件,而训练出来的模型要满足这些限制条件,这个模型应该是满足所给条件的最大熵模型,因此设计最大熵模型的训练方法都可以在这里使用。
最后,需要指明结构的训练和参数的训练通常是交互进行的。也就是先优化参数,再优化结构,再优化参数,直至得到收敛或者误差足够小的模型。