线段树及其应用

发表于 更新于 分类于 Waline：

线段树简介

线段树（Segment Tree）是一种非常灵活的数据结构，它能够高效处理与区间相关的问题，如区间求和、区间最大值（或最小值）以及区间更新等操作。

线段树是一个二叉树，其中每个节点代表一个区间（或一个段），并且这个区间可以被分解成两个子区间，这些子区间分别由当前节点的两个子节点所表示。

线段树的思想源自于二叉搜索树，都有区间的概念，不过BST的节点是区间分割点，而线段树的节点本身就是区间的整体信息，这个整体信息可以是任何该区间的整体信息，只要该区间的整体信息可以由两个子区间的整体信息合并来即可，如区间和

基本特性

线段树的每个节点都代表一个区间。

线段树的唯一根节点，代表整个[1, n]区间。

线段树的每个叶节点，都代表长度为1的区间[x, x]。

对于每个内部节点[l, r]，它的左节点[l, mid]，右节点[mid+1, r]，其中m i d = ⌊ (l + r) / 2 ⌋

线段树除去最后一层，是一个满二叉树。

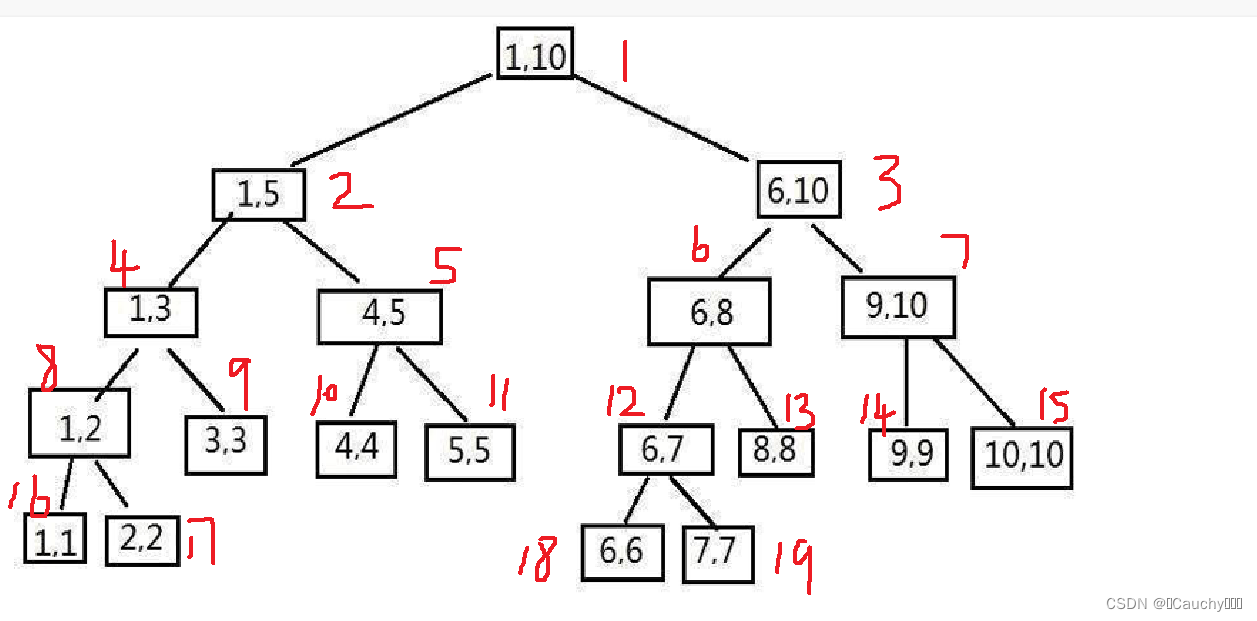
可以发现树的最后一层节点在数组中存储，位置是不连续的。理想情况下：n 个节点的满二叉树有2∗n−1个节点，但由于最后一层产生空余，为了要保证数组能存储整棵树，最后一层也要开到2 ∗ n的空间。因此一共需要开辟4n的空间存储线段树。

使用场景

线段树的使用场景非常广泛，主要集中在对区间数据进行快速查询和更新上，以下是一些常见的应用场景：

区间查询：查询一个区间内的最大值、最小值或者区间值的和。例如，在股票市场分析中，可能需要查询某个时间段内的最高股价或者平均股价。

区间更新：在某个区间内更新一个或多个值，而且这些更新可能是增加、减少或者赋新值等操作。线段树可以在对数时间内完成这些操作，并且能够保持区间查询的正确性。

懒惰传递：这是线段树的一个高级特性，允许节点延迟更新。当对一个区间进行更新操作时，并不立即更新所有相关节点，而是仅标记这个区间，当需要查询时再进行实际的更新。这样可以大大提高批量更新操作的效率。

动态查询：不仅仅限于静态数据，线段树也能够适用于数据动态变化的情况，比如数据集合中新增或删除数据，线段树可以相应地调整，以维护查询和更新的准确性和效率。

示例

一个典型的应用实例是对于一个长度为nn的数组，支持以下两种操作：

  1. 更新操作：更新数组的某个元素或某个区间内的所有元素。

  2. 查询操作：查询数组中某个区间（比如LL到RR）的和、最大或最小值。

使用普通的数组或链表，这些操作的时间复杂度可能是线性的，即O(n)O(n)。利用线段树，可以将更新和查询操作的时间复杂度降低到O(log⁡n)O(\log n)，从而能够处理更大规模的数据，或者更频繁的查询和更新请求。

总之，线段树是处理区间查询和修改问题的有力工具，特别是当涉及到频繁的修改和需要快速响应查询时，线段树提供了一个非常有效的解决方案。

线段树的JS实现

树的建立（build）

  1. 先开辟4n大小的数组空间
  2. 从根节点开始建立，根节点表示[1, n]
  3. 递归的二分构建左子树[l, mid]，右子树[mid + 1, r]
  4. 向下递归到叶子节点结束，叶节点维护区间[x, x]，存储 $ a_x $的值
  5. 回溯过程中，从下往上更新信息，即 val(l,r) = fn(val(l, mid), val(mid + 1, r))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class SegmentTree {
  constructor(arr, fn) {
    this.inputArray = [...arr];
    this.n = arr.length;
    this.tree = new Array(this.n * 4).fill(0);
    this.lazy = new Array(this.n * 4).fill(0);
    this.fn = fn;
    this.build(1, 0, this.n - 1);
  }

  // buid函数的作用是，将arr中下标在[left, rigth]之间的数据的fn的结算结果存储在tree数组索引为treeIndex的位置
  build(arr, left, right, treeIndex) {
    if (left === right) {
      this.tree[treeIndex] = arr[left];
      return;
    }
    const mid = left + Math.floor((right - left) / 2);
    this.build(arr, left, mid, treeIndex * 2 + 1);
    this.build(arr, mid + 1, right, treeIndex * 2 + 2);
    this.tree[treeIndex] = this.fn(this.tree[treeIndex * 2 + 1], this.tree[treeIndex * 2 + 2]);
  }
}

树的更新（懒惰传递更新）

单点更新

更新arr数组中索引为index的值为val

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
updateSingleNode(index, val, node = 1, start = 0, end = this.n - 1) {
  if (this.lazy[node] !== 0) {
    let dx = this.lazy[node];
    this.lazy[node] = 0;
    this.tree[node] += dx * (end - start + 1);
    if (start !== end) {
      this.lazy[2 * node] += dx;
      this.lazy[2 * node + 1] += dx;
    }
  }
  
  if (start === end) {
    this.tree[node] = val;
    return;
  }
  
  let mid = Math.floor((start + end) / 2);
  if (index <= mid) {
    this.updateSingleNode(index, val, 2 * node, start, mid);
  } else {
    this.updateSingleNode(index, val, 2 * node + 1, mid + 1, end);
  }
  
  this.tree[node] = this.fn(this.tree[2 * node], this.tree[2 * node + 1]);
}

这其中涉及了懒惰更新，可能大家会有疑问，哪里懒惰更新了，明明每次递归都有处理lazy的数据

其实，注意看，每次处理完当前的lazy数据后，都会将变化同时传递给左子节点和右子节点的lazy，也就是这段代码

1
2
3
4
if (start !== end) {
  this.lazy[2 * node] += dx;
  this.lazy[2 * node + 1] += dx;
}

但其实，如果要更新的节点只会存在于其中的一个子树中，另一个子树的更新确实没有在本次更新中实际去更新，这样就可以做到，每次更新不需要遍历整个线段树

区间更新

更新inputArray中索引在[l, r]之间的数据为val

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
updateRange(node, start, end, l, r, val) {
  // 懒惰更新
  if (this.lazy[node] !== 0) {
    let dx = this.lazy[node];
    this.lazy[node] = 0;
    this.tree[node] += dx * (end - start + 1);
    if (start !== end) {
      this.lazy[node * 2] += dx;
      this.lazy[node * 2 + 1] += dx;
    }
  }

  if (start > end || start > r || end < l) return;

  // 当前node指向的tree节点对应的inputArray是[start, end]
  // 如果[start, end]被 要更新的区域[l ,r]覆盖，则更新node指向的tree节点，并设置node子节点懒惰更新
  // 然后直接返回，并不需要继续更新node的子节点了，因为已经设置懒惰更新了
  if (start >= l && end <= r) {
    this.tree[node] += (end - start + 1) * val;
    if (start !== end) {
      this.lazy[node * 2] += val;
      this.lazy[node * 2 + 1] += val;
    }
    return;
  }

  // 如果[start, end]不能被要更新的区域[l ,r]覆盖
  // 这意味着node指向的节点中是有部分节点不应该被本次更新影响的，所以不能直接设置左右子节点懒惰更新，而要继续去计算
  let mid = Math.floor((start + end) / 2);
  this.updateRange(node * 2, start, mid, l, r, val);
  this.updateRange(node * 2 + 1, mid + 1, end, l, r, val);
  this.tree[node] = this.fn(this.tree[2 * node], this.tree[2 * node + 1]);
}

查询（懒惰传递更新）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
query(node, start, end, l, r) {
  if (start > r || end < l) {
    return 0;
  }

  if (this.lazy[node] !== 0) {
    let dx = this.lazy[node];
    this.lazy[node] = 0;
    this.tree[node] += dx * (end - start + 1);
    if (start !== end) {
      this.lazy[node * 2] += dx;
      this.lazy[node * 2 + 1] += dx;
    }
  }

  if (start >= l && end <= r) {
    return this.tree[node];
  }

  let mid = Math.floor((start + end) / 2);
  let p1 = this.query(node * 2, start, mid, l, r);
  let p2 = this.query(node * 2 + 1, mid + 1, end, l, r);
  return this.fn(p1, p2);
}

懒惰传递更新

大家可以发现，在更新和查询的操作中有一段完全相同的代码，这段代码就是用来懒惰传递更新的

1
2
3
4
5
6
7
8
9
if (this.lazy[node] !== 0) {
  let dx = this.lazy[node];
  this.lazy[node] = 0;
  this.tree[node] += dx * (end - start + 1);
  if (start !== end) {
    this.lazy[node * 2] += dx;
    this.lazy[node * 2 + 1] += dx;
  }
}

所谓的懒惰更新，其实是因为，每次更新都会影响到整个树的中一半节点的值，但其实更新到的节点并不一定会立即用到，我们可以先把这些先把当前要更新的值存下来，等到真的查询到的时候再一次性把多次更新的结果一并应用到tree节点上

具体的方案就是：

  1. 当需要更新某个tree节点的时候，但是不去具体修改，等真的要查询的时候，再修改当前tree的节点的值，并且同时标记当前tree节点的子节点要更新
  2. 等到真正查询到子节点的时候再在子节点上递归应用上述操作

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
class SegmentTree {
  constructor(arr, fn) {
    this.inputArray = [...arr];
    this.fn = fn
    this.n = arr.length;
    this.tree = new Array(this.n * 4).fill(0);
    this.lazy = new Array(this.n * 4).fill(0);
    this.build(1, 0, this.n - 1);
  }

  build(node, start, end) {
    if (start === end) {
      this.tree[node] = this.inputArray[start];
    } else {
      let mid = Math.floor((start + end) / 2);
      this.build(2 * node, start, mid);
      this.build(2 * node + 1, mid + 1, end);
      this.tree[node] = this.fn(this.tree[2 * node], this.tree[2 * node + 1]);
    }
  }

  updateSingleNode(index, val, node = 1, start = 0, end = this.n - 1) {
    if (this.lazy[node] !== 0) {
      let dx = this.lazy[node];
      this.lazy[node] = 0;
      this.tree[node] += dx * (end - start + 1);
      if (start !== end) {
        this.lazy[2 * node] += dx;
        this.lazy[2 * node + 1] += dx;
      }
    }
    
    if (start === end) {
      this.tree[node] = val;
      return;
    }
    
    let mid = Math.floor((start + end) / 2);
    if (index <= mid) {
      this.updateSingleNode(index, val, 2 * node, start, mid);
    } else {
      this.updateSingleNode(index, val, 2 * node + 1, mid + 1, end);
    }
    
    this.tree[node] = this.fn(this.tree[2 * node], this.tree[2 * node + 1]);
  }

  updateRange(node, start, end, l, r, val) {
    if (this.lazy[node] !== 0) {
      let dx = this.lazy[node];
      this.lazy[node] = 0;
      this.tree[node] += dx * (end - start + 1);
      if (start !== end) {
        this.lazy[node * 2] += dx;
        this.lazy[node * 2 + 1] += dx;
      }
    }

    if (start > end || start > r || end < l) return;

    if (start >= l && end <= r) {
      this.tree[node] += (end - start + 1) * val;
      if (start !== end) {
        this.lazy[node * 2] += val;
        this.lazy[node * 2 + 1] += val;
      }
      return;
    }

    let mid = Math.floor((start + end) / 2);
    this.updateRange(node * 2, start, mid, l, r, val);
    this.updateRange(node * 2 + 1, mid + 1, end, l, r, val);
    this.tree[node] = this.fn(this.tree[2 * node], this.tree[2 * node + 1]);
  }

  query(node, start, end, l, r) {
    if (start > r || end < l) {
      return 0;
    }

    if (this.lazy[node] !== 0) {
      let dx = this.lazy[node];
      this.lazy[node] = 0;
      this.tree[node] += dx * (end - start + 1);
      if (start !== end) {
        this.lazy[node * 2] += dx;
        this.lazy[node * 2 + 1] += dx;
      }
    }

    if (start >= l && end <= r) {
      return this.tree[node];
    }

    let mid = Math.floor((start + end) / 2);
    let p1 = this.query(node * 2, start, mid, l, r);
    let p2 = this.query(node * 2 + 1, mid + 1, end, l, r);
    return this.fn(p1, p2);
  }
}

// 示例使用
const inputArray = [1, 3, 5, 7, 9, 11];
const segTree = new SegmentTree(inputArray, (a, b) => a + b);

// 单点更新示例
segTree.updateSingleNode(3, 10); // 将index=3的元素更新为10
console.log(segTree.query(1, 0, inputArray.length - 1, 1, 3));