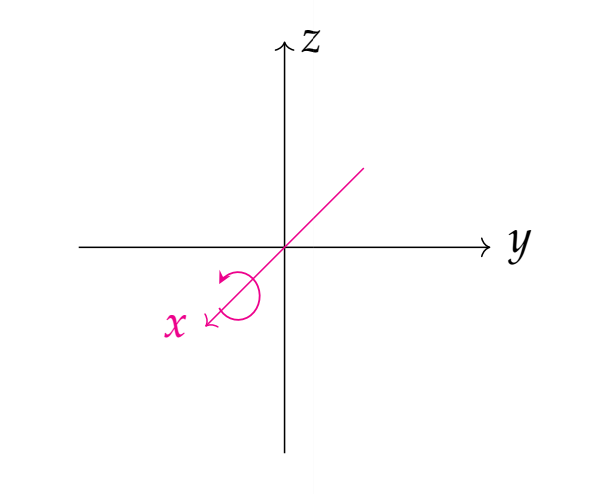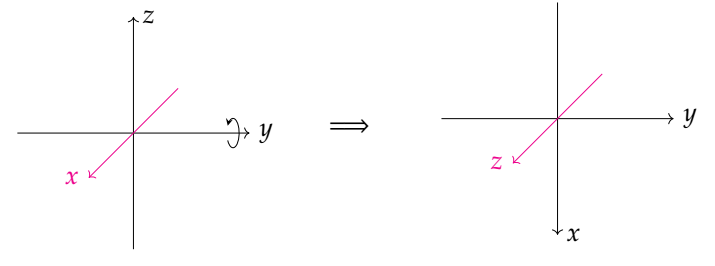这次一定要搞明白万向锁是个什么东西。本文会按照以下顺序慢慢展开:
通过一个简单的可以实际操作的例子告诉大家,万向锁在我们生活中的表现 什么是万向锁 分别从矩阵和几何的角度讲一下万向锁存在的原理 万向锁到底有什么问题 为什么四元数可以解决万向锁的问题 可以拿出手机放在桌面上,屏幕朝上,手机的最长边垂直与桌子的边缘设置为X轴,这个时候屏幕的短边平行于桌子的边缘设置为Y轴,因此垂直与屏幕的向量为Z轴。
我们先绕手机的最长边X轴顺时针旋转30度,这个时候手机离开桌面,留下一个长边与桌子接触;然后再绕Y轴,也就是手机的短边旋转90度,让屏幕面与桌子的边缘平行;
再绕Z轴旋转10度,也就是绕垂直于屏幕的轴旋转10度,这个时候你会发现,绕Z轴旋转时,屏幕面还是平行桌子的边缘,而此时绕Z轴旋转的角度给手机姿态带来的影响和最开始旋转X轴给手机姿态带来的影响是一样的——都是使手机最终的姿态(已经绕Y轴旋转了90度使得手机屏幕与桌子边缘平行)为绕着垂直于屏幕的轴旋转一定的角度。
也就是说,你完全可以不用绕Z轴旋转,通过调节绕X轴旋转的角度数,使得最终手机的姿态和上述旋转过程达到的姿态一样。
或者说,一旦Y轴转了90度,你的手机平面一定在与桌面垂直的平面内,无论你一开始如何绕X轴转,以及最后如何绕Z轴转
在解释万向锁之前简单讲一下欧拉角。
这个概念我们其实都接触过,但是可能没有那么深入,所以在这里再解释一下:
莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于任何参考系,一个刚体的取向,是依照顺序,从这参考系,做三个欧拉角的旋转而设定的。所以,刚体的取向可以用三个基本旋转矩阵来决定。换句话说,任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。
它分为静态的欧拉角和动态的欧拉角
1,静态:即绕世界坐标系三个轴的旋转,由于物体旋转过程中坐标轴保持静止,所以称为静态。
2,动态:即绕物体坐标系三个轴的旋转,由于物体旋转过程中坐标轴随着物体做相同的转动,所以称为动态。
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系(固定系)又称为实验室参考系,是静止不动的。而坐标系(固连系)则固定于刚体,随着刚体的旋转而旋转。
参阅右图。设定xyz-轴为参考系的参考轴。称xy-平面与XY-平面的相交为交点线,用英文字母(N)代表。zxz顺规的欧拉角可以静态地这样定义:
α \alpha α β \beta β γ \gamma γ
对于夹角的顺序和标记,夹角的两个轴的指定,并没有任何常规。科学家对此从未达成共识。每当用到欧拉角时,我们必须明确的表示出夹角的顺序,指定其参考轴。
角值范围
α \alpha α γ \gamma γ 2 π 2\pi 2 π β \beta β π \pi π
两组欧拉角的α \alpha α 2 π 2\pi 2 π β \beta β γ \gamma γ 两组欧拉角的γ \gamma γ 2 π 2\pi 2 π α \alpha α β \beta β 前面提到,设定刚体取向的旋转矩阵{\displaystyle [\mathbf {R} ]}[\mathbf{R}]是由三个基本旋转矩阵合成的:
[ R ] = [ c o s γ s i n γ 0 − s i n γ c o s γ 0 0 0 1 ] [ 1 0 0 0 c o s β s i n β 0 − s i n β c o s β ] [ c o s α s i n α 0 − s i n α c o s α 0 0 0 1 ] [R] = \begin{bmatrix} cos\gamma & sin\gamma & 0 \\ -sin\gamma & cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\beta & sin\beta \\ 0 & -sin\beta & cos\beta \end{bmatrix} \begin{bmatrix} cos\alpha & sin\alpha & 0 \\ -sin\alpha & cos\alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} [ R ] = ⎣ ⎢ ⎡ c o s γ − s i n γ 0 s i n γ c o s γ 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 0 0 0 c o s β − s i n β 0 s i n β c o s β ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ c o s α − s i n α 0 s i n α c o s α 0 0 0 1 ⎦ ⎥ ⎤
经过运算之后的结果为
[ R ] = [ c o s α c o s γ − c o s β s i n α s i n γ s i n α c o s γ + c o s β c o s α s i n γ s i n β s i n γ − c o s α s i n γ − c o s β s i n α c o s γ − s i n α s i n γ + c o s β c o s α c o s γ s i n β c o s γ s i n β s i n α − s i n β c o s α c o s β ] [R] = \begin{bmatrix} cos\alpha cos\gamma - cos\beta sin\alpha sin\gamma & sin\alpha cos\gamma + cos\beta cos\alpha sin\gamma & sin\beta sin\gamma \\ -cos\alpha sin\gamma - cos\beta sin\alpha cos\gamma & -sin\alpha sin\gamma + cos\beta cos\alpha cos\gamma & sin\beta cos\gamma \\ sin\beta sin\alpha & -sin\beta cos\alpha & cos\beta \end{bmatrix} [ R ] = ⎣ ⎢ ⎡ c o s α c o s γ − c o s β s i n α s i n γ − c o s α s i n γ − c o s β s i n α c o s γ s i n β s i n α s i n α c o s γ + c o s β c o s α s i n γ − s i n α s i n γ + c o s β c o s α c o s γ − s i n β c o s α s i n β s i n γ s i n β c o s γ c o s β ⎦ ⎥ ⎤
在经典力学里,时常用zxz顺规来设定欧拉角;照着第二个转动轴的轴名,简称为x顺规。另外,还有别种欧拉角组。合法的欧拉角组中,唯一的限制是,任何两个连续的旋转,必须绕着不同的转动轴旋转。因此,一共有12种顺规。例如,y顺规,第二个转动轴是y-轴,时常用在量子力学、核子物理学、粒子物理学。另外,还有一种顺规,xyz顺规,是用在航空航天工程学;参阅泰特-布莱恩角
我们也可以给予欧拉角两种不同的动态定义。一种是绕着固定于刚体的坐标轴的三个旋转的复合;另外一种是绕着实验室参考轴的三个旋转的复合。用动态的定义,我们能更了解,欧拉角在物理上的含义与应用。特别注意,以下的描述, XYZ坐标轴是旋转的刚体坐标轴;而xyz坐标轴是静止不动的实验室参考轴。
绕着XYZ坐标轴旋转:最初,两个坐标系统xyz与XYZ的坐标轴都是重叠着的。开始先绕着Z-轴旋转α \alpha α β \beta β γ \gamma γ
绕着xyz坐标轴旋转:最初,两个坐标系统xyz与XYZ的坐标轴都是重叠着的。开始先绕着z-轴旋转γ \gamma γ β \beta β α \alpha α
我们了解了欧拉角分为静态欧拉角和动态欧拉角,我们在继续看看什么是万向锁。
首先我们先直观地理解一点,万向锁只会产生在动态欧拉角,也就是我们是绕物体自身的坐标系旋转的,物体自身的坐标系会随着物体的旋转一起旋转
通过上面那个小实验,我们可以大致这样理解,所以万向锁之所以叫做锁,是因为有两个维度的旋转效果重叠了,即旋转X轴的效果和完全可以通过旋转Z轴来实现,也就是丢失了一个维度.
但是从另一个角度讲,这个“锁”的意思并不是说欧拉角有什么不能够表示出来的角度,而是如果你的章动角是90度的话你最终的结果一定是在某个平面上的 。
我们首先看一下下面这个图,这个图的坐标系既是物体自身坐标轴,和世界坐标轴完全一样
我们首先绕x轴旋转一个角度,没有什么问题
然后我们再绕y轴旋转90度
这个时候可以看到z轴变成了原来x轴的方向,这个时候我们绕物体自身的z轴转,从世界坐标上来看,就是绕初始状态的x轴在转,也就是说从世界坐标系上看来,一开始绕物体自身的x轴,和最后绕物体自身的z轴转,都是一样的,都是绕世界坐标系的x轴转
上述过程用矩阵的乘法形式写出来就是
R z ( β ) R y ( π / 2 ) R x ( α ) = [ c o s β − s i n β 0 s i n β c o s β 0 0 0 1 ] [ 0 0 1 0 1 0 − 1 0 0 ] [ 1 0 0 0 c o s α − s i n α 0 s i n α c o s α ] = [ 0 s i n ( α − β ) c o s ( α − β ) 0 c o n ( α − β ) − s i n ( α − β ) − 1 0 0 ] = [ 0 0 1 0 1 0 − 1 0 0 ] [ 1 0 0 0 c o s ( α − β ) − s i n ( α − β ) 0 s i n ( α − β ) c o s ( α − β ) ] = R y ( π / 2 ) R x ( α − β ) R_z(\beta)R_y(\pi / 2)R_x(\alpha) \\ =\begin{bmatrix} cos\beta & -sin\beta & 0 \\ sin\beta & cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha \\ 0 & sin\alpha & cos\alpha \end{bmatrix} \\ = \begin{bmatrix} 0 & sin(\alpha - \beta) & cos(\alpha - \beta) \\ 0 & con(\alpha - \beta) & -sin(\alpha - \beta) \\ -1 & 0 & 0 \end{bmatrix} \\ = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha - \beta) & -sin(\alpha - \beta) \\ 0 & sin(\alpha - \beta) & cos(\alpha - \beta) \end{bmatrix} \\ = R_y(\pi /2)R_x(\alpha - \beta) R z ( β ) R y ( π / 2 ) R x ( α ) = ⎣ ⎢ ⎡ c o s β s i n β 0 − s i n β c o s β 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 0 0 − 1 0 1 0 1 0 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 0 0 0 c o s α s i n α 0 − s i n α c o s α ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 − 1 s i n ( α − β ) c o n ( α − β ) 0 c o s ( α − β ) − s i n ( α − β ) 0 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 − 1 0 1 0 1 0 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 0 0 0 c o s ( α − β ) s i n ( α − β ) 0 − s i n ( α − β ) c o s ( α − β ) ⎦ ⎥ ⎤ = R y ( π / 2 ) R x ( α − β )
所以万向锁并不是不能表示空间中的某个角位移,而是因为万向锁,角位移之间的插值变得不如意,那么万向锁是怎么出现的呢?第二个旋转的角度为90度的时候,使用第一个轴与第三个轴相重合,这是从感性的角度去认识这个现象,如果从数学的角度去解释,那就是cos90=0
在游戏中,当角色旋转的动画触发时,角色就会做一系列连续的旋转变换,每一个变换都要用一组欧拉角来表示,但是不可能把每一个方位的欧拉角都存储起来,因此动画师定义了一系列关键帧,指定关键帧处角色的方位(用一组欧拉角描述),然后计算机根据时间t对这几组欧拉角进行插值,得到一系列欧拉角。
如果pitch不是±90°,就不会出现万向锁现象,插值后的一系列欧拉角完全可以刻画出我们所期望的角色旋转路径。
如果某个关键帧的pitch即绕第二个轴的旋转为90°,就会遇到万向锁,这时手机只能在水平面内旋转,如果动画师指定下一个关键帧手机的方位不是立起来的,没有任何问题,但如果指定的下一个关键帧的方位是立起来的,会出现什么情况呢?
要解决这个问题,首先要问一下,万向锁问题存在的前提条件
我们前面知道了,万向锁只存在于动态欧拉角,即物体绕自身坐标系旋转,且自身坐标系会随着自身的旋转一起旋转,它表现为Y轴旋转90度的话,X轴和Z轴的旋转效果是相通的。
换个角度想,其实就是在欧拉角下,同样的效果有多种不同的旋转方式,导致插值的时侯结果不确定。
那要解决这个问题,其实思路也比较明确,就是换个表示方法,在这个新的表示方法中,一个旋转结果的表示方法是唯一的。
我们给出另一种表述方向的方法:轴角表示(Axis-Angle-Representation)。跟欧拉角不同的是,我们这次不再采取多次旋转的方式来找到目标方向,而是找到一根旋转轴,只通过绕这根轴旋转一次就可以得到目标方向。这样就不会产生问题了吗?是的,证明方法很简单,首先以目标矩阵原点为一角,三轴为三边建立一个立方体,这个立方体中通过原点的对角线就是我们要找的旋转轴,显然,这个旋转轴是唯一的,而我们知道,绕一个旋转轴旋转不同角度,对应的方向也是不同的(角度范围 (−π,π]),由此可见,空间中任一位置的轴角表示是唯一的。
一般来说,轴角表示方向时,会出现4个参数,其中3个用于表示旋转轴,1个用于表示旋转角大小。而如果我们规定了表示旋转轴的向量为单位向量 e ,考虑到x 2 + y 2 + z 2 = 1 \sqrt{x^2+y^2+z^2}=1 x 2 + y 2 + z 2 = 1 θ = θ e \bm{\theta} = \theta e θ = θ e
从矩阵角度考虑这个东西的存在也是可以的,矩阵中有个相似矩阵和特征向量的概念,大家可以理解这个旋转轴就是欧拉角旋转矩阵的特征向量,这个旋转轴的旋转角度就是该特征向量的特征值。
四元数是复数,更具体地说四元数是存在三个虚部的复数。q=w+ix+jy+kz,其中i,j,k是虚数单位,满足 i2=j 2=k^2 = -1,且 i⋅j=k,j⋅i=k 。
q 1 + q 2 = ( w 1 + w 2 ) + i ( x 1 + x 2 ) + j ( y 1 + y 2 ) + k ( z 1 + z 2 ) = [ ( w 1 + 2 2 ) , ( v 1 + v 2 ) ] q 1 ⋅ q 2 = ( w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 ) + i ( w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 ) + j ( w 1 y 2 − x 1 z 2 + y 1 w 2 + z 1 x 2 ) + k ( w 1 z 2 + x 1 y 2 − y z x 2 + z 1 w 2 ) q_1 + q_2 = (w_1 + w_2) + i(x_1 + x_2) + j(y_1 + y_2) + k(z_1 +z_2) = [(w_1 + 2_2), (v_1 +v_2)] \\ q_1 \cdot q_2 = (w_1w_2 -x_1x_2 - y_1y_2 - z_1z_2) + \\ i(w_1x_2 + x_1w_2 + y_1z_2 - z1y_2) + \\ j(w_1y_2 - x_1z_2 + y_1w_2 + z_1x_2) + \\ k(w_1z_2 + x_1y_2 -y_zx_2 + z_1w_2) q 1 + q 2 = ( w 1 + w 2 ) + i ( x 1 + x 2 ) + j ( y 1 + y 2 ) + k ( z 1 + z 2 ) = [ ( w 1 + 2 2 ) , ( v 1 + v 2 ) ] q 1 ⋅ q 2 = ( w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 ) + i ( w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 ) + j ( w 1 y 2 − x 1 z 2 + y 1 w 2 + z 1 x 2 ) + k ( w 1 z 2 + x 1 y 2 − y z x 2 + z 1 w 2 )
将四元数用于计算轴角表示运算时,我们通常写成向量形式(vector representation) ,q = [ w , v ⃗ ] = [ w , ( x y z ) ] q=\begin{bmatrix} w, \vec v \end{bmatrix}=\begin{bmatrix} w, \begin{pmatrix} x \\ y \\ z \end{pmatrix} \end{bmatrix} q = [ w , v ] = ⎣ ⎢ ⎡ w , ⎝ ⎛ x y z ⎠ ⎞ ⎦ ⎥ ⎤ w 2 + x 2 + y 2 + z 2 = 1 w^2+x^2+y^2+z^2 = 1 w 2 + x 2 + y 2 + z 2 = 1
q 1 ⋅ q 2 = [ w 1 , v ⃗ 1 ] ⋅ [ w 2 , v ⃗ 2 ] = [ w 1 w 2 − v 1 v 2 , v 1 × v 2 + w 1 ⋅ v 2 + w 2 ⋅ v 1 ] q_1 \cdot q_2 = [w_1, \vec v_1] \cdot [w_2, \vec v_2] = [w_1w_2 - v_1v_2, v1 \times v_2 + w_1 \cdot v_2 + w_2 \cdot v_1] q 1 ⋅ q 2 = [ w 1 , v 1 ] ⋅ [ w 2 , v 2 ] = [ w 1 w 2 − v 1 v 2 , v 1 × v 2 + w 1 ⋅ v 2 + w 2 ⋅ v 1 ]
或者我们也可以写成矩阵的形式
q 1 q 2 = [ w 1 − x 1 − y 1 − z 1 x 1 w 1 − z 1 y 1 y 1 z 1 w 1 − x 1 z 1 − y 1 x 1 w 1 ] [ w 2 x 2 y 2 z 2 ] q_1q_2 = \begin{bmatrix} w_1 & -x_1 & -y_1 & -z_1 \\ x_1 & w_1 & -z_1 & y_1 \\ y_1 & z_1 & w_1 & -x_1 \\ z_1 & -y_1 & x_1 & w_1 \end{bmatrix} \begin{bmatrix} w_2 \\ x_2 \\ y_2 \\ z_2 \end{bmatrix} q 1 q 2 = ⎣ ⎢ ⎢ ⎢ ⎡ w 1 x 1 y 1 z 1 − x 1 w 1 z 1 − y 1 − y 1 − z 1 w 1 x 1 − z 1 y 1 − x 1 w 1 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ w 2 x 2 y 2 z 2 ⎦ ⎥ ⎥ ⎥ ⎤
观察此式,我们发现两个四元数相乘,需要存储8个单位的数据,也就是说,每个参与运算的四元数只要存储4个单位数据即可。此外还需要几个特殊的性质:
四元数模∣ ∣ q ∣ ∣ = w 2 + x 2 + y 2 + z 2 ||q|| = \sqrt{w^2 + x^2 + y^2 + z^2} ∣ ∣ q ∣ ∣ = w 2 + x 2 + y 2 + z 2 四元数共轭q ∗ = ( w + i x + j y + k z ) ∗ = w − i x − j y − k z q^{*} = (w + ix + jy + kz)^{*}= w -ix -jy - kz q ∗ = ( w + i x + j y + k z ) ∗ = w − i x − j y − k z 共轭的向量形式q ∗ = ( [ w v ⃗ ] ) ∗ = [ w − v ⃗ ] q^{*} = (\begin{bmatrix} w & \vec v \end{bmatrix})^{*} = \begin{bmatrix} w & -\vec v \end{bmatrix} q ∗ = ( [ w v ] ) ∗ = [ w − v ] 四元数的倒数:q ⋅ q − 1 = q − 1 ⋅ q = 1 q \cdot q^{-1} = q^{-1} \cdot q = 1 q ⋅ q − 1 = q − 1 ⋅ q = 1 共轭与倒数的关系:q − 1 = q ∗ w 2 + x 2 + y 2 + z 2 q^{-1}=\frac{q^*}{w^2+x^2+y^2+z^2} q − 1 = w 2 + x 2 + y 2 + z 2 q ∗ q ∗ = q − 1 q^{*} = q{-1} q ∗ = q − 1 四元数运算同时满足结合律和分配律,不符合交换律 了解了上面的计算法则,我们就可以利用四元数来计算方向变换过程了。还记得我们之前说过计算时四元数我们用向量形式表示,且保证它是单位四元数吗?其实四元数的向量形式我们还可以进一步改写为极形式(polar representation),q = ∥ q ∥ [ c o s θ , n ⃗ ⋅ s i n θ ] q = \|q\|[cos\theta, \vec{n}\cdot sin\theta] q = ∥ q ∥ [ c o s θ , n ⋅ s i n θ ]
其中 ‖q‖ 代表了四元数的模,单位四元数模为1,而 θ 是四元数表示的旋转过程的半角大小,也就是说(2θ) 就是旋转角大小, n 则是表示旋转轴方向的单位向量。用这种表示方法,四元数即可表示任意轴角表达的方向变换。
先将原向量坐标表示为四元数p = [ 0 , v ⃗ ] p=[0,\vec{v}] p = [ 0 , v ] r = q ⋅ p ⋅ q ∗ r = q\cdot p\cdot q^* r = q ⋅ p ⋅ q ∗ r = q ⋅ p ⋅ q − 1 r = q \cdot p\cdot q^{-1} r = q ⋅ p ⋅ q − 1
其实四元数就是为了更好地表示旋转轴和旋转角度而已,旋转轴是个三维向量,加上旋转角度就变成四维了。而选择四元数来表示是因为它的一些特性。
先说结论,四元数的引用是为了减少计算量和计算时存储占用的空间。
但是,如果你足够细心,一定可以发现两个四元数相乘的过程其实是一个4×4矩阵与一个4×1矩阵相乘的过程,而四元数计算一次变换需要两次这个过程,其中包括24次加法运算和32次乘法运算,反观欧拉角的矩阵变换只要进行一次3×3矩阵和3×1矩阵的乘法运算,其中包括6次加法运算和9次乘法运算,运算量明显是四元数更大一些。如果你再细心一些可以发现,四元数运算时虽然有个4×4矩阵参与运算,但是矩阵中的每一项都是已经存储过的单位数据,而参与欧拉角运算的3×3矩阵则要通过另外已存储的单位数据进行的16次乘法运算,4次加法运算以及4次符号改变运算来求出,不过即使加上这些运算过程,矩阵运算也只要25次乘法运算,10次加法运算以及4次符号改变运算,运算量上来说,欧拉角的矩阵运算依然比四元数运算要有优势。但事实上,我们一般遇到的运动学问题很少会有只做一次方向转换的情况出现,对于复杂的系统和机器人来说,我们往往会面对数量庞大的转变方向过程。这种情况下四元数的优势就体现出来了,我们考虑多次变换的四元数运算(利用上面极坐标形式):
R = R 1 R 2 . . . R n − 1 R n = ( q n ( q n − 1 . . . ( q 2 ( q 1 p q 1 ∗ ) q 2 ∗ ) . . . q n − 1 ∗ ) q n ∗ ) R = R_1R_2...R_{n-1}R_n = (q_n(q_{n-1}...(q_2(q_1pq^*_1)q^*_2)...q^*_{n-1})q^*_n) R = R 1 R 2 . . . R n − 1 R n = ( q n ( q n − 1 . . . ( q 2 ( q 1 p q 1 ∗ ) q 2 ∗ ) . . . q n − 1 ∗ ) q n ∗ )
利用结合律:
R = R 1 R 2 . . . R n − 1 R n = ( q n q n − 1 . . . q 2 q 1 ) p ( q 1 ∗ q 2 ∗ . . . q n − 1 ∗ q n ∗ ) R = R_1R_2...R_{n-1}R_n = (q_nq_{n-1}...q_2q_1)p(q^*_1q^*_2...q^*_{n-1}q^*_n) R = R 1 R 2 . . . R n − 1 R n = ( q n q n − 1 . . . q 2 q 1 ) p ( q 1 ∗ q 2 ∗ . . . q n − 1 ∗ q n ∗ )
考虑四元数的共轭( q a q b ) ∗ = q b ∗ q a ∗ (q_aq_b)^* = q^*_bq^*_a ( q a q b ) ∗ = q b ∗ q a ∗
R = R 1 R 2 . . . R n − 1 R n = ( q n q n − 1 . . . q 2 q 1 ) p ( q n q n − 1 . . . q 2 q 1 ) ∗ R = R_1R_2...R_{n-1}R_n = (q_nq_{n-1}...q_2q_1)p(q_nq_{n-1}...q_2q_1)^* R = R 1 R 2 . . . R n − 1 R n = ( q n q n − 1 . . . q 2 q 1 ) p ( q n q n − 1 . . . q 2 q 1 ) ∗
可以发现,原向量 ppp 左右两侧括号里的运算结果是一对共轭四元数,也就是说可以利用3次易号运算代替n次四元数相乘运算,大大减少了计算量。
最后稍微提一嘴,很多接触这个问题的人都是游戏开发者,可能会有疑问,为什么在Unity的Inspector中没有这个问题,这个大家可以去试试,Unity的Inspector中Y轴不是物体自身坐标轴旋转,所以万向锁就被解了,具体Unity内部的旋转是怎么回事可以看下一篇博客,这里挖个坑
参考文章:
欧拉角 - 维基百科
如何通俗地解释欧拉角?之后为何要引入四元数?