矩形区域不超过 K 的最大数值和

发表于 更新于 分类于 Waline：

今天leetcode的每日一题是一道困难的题目，但我总结一下他不是因为它的难度，而是这是一道结合了前缀和的变体以及二叉搜索树的题目，可以帮我回顾一下。

首先是题目链接：https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/

暴力枚举

首先上来我们很容易想到，暴力枚举所有的子矩阵，那么这个时候的复杂度是O(m^2 * n^2)，这样很容易超时。不过这是基本思路，我们来一步步优化

朴素二维前缀和

在暴力枚举的过程中，其实很多计算我们都做过了。

我们可以定义sum[i][j]为从（0,0）到（i，j）所有单元格值的和

那么，sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i][j]

因此当我们要求 (x1, y1) 作为左上角，(x2, y2) 作为右下角 的区域和的时候，可以直接利用前缀和数组快速求解：

sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]

这样一来我们就可以先通过O(m * n)来初始化前缀和数组，再通过O(m * n)来计算所有子矩阵的和，这样就把时间复杂度降低到了O(m * n);

主体解题思路（将二维前缀和抽象为一维）

我们来细想一下「朴素二维前缀和」解法是如何搜索答案（子矩阵）：通过枚举「左上角」&「右下角」来唯一确定某个矩阵。

换句话说是通过枚举 (i,j)(i,j) 和 (p,q)(p,q) 来唯一确定子矩阵的四条边，每个坐标点可以看作确定子矩阵的某条边。

既然要确定的边有四条，我们可以如何降低复杂度呢？

我们可以枚举其中三条边，然后使用数据结构来加速找第四条边。

当我们确定了三条边（红色）之后，形成的子矩阵就单纯取决于第四条边的位置（黄色）：

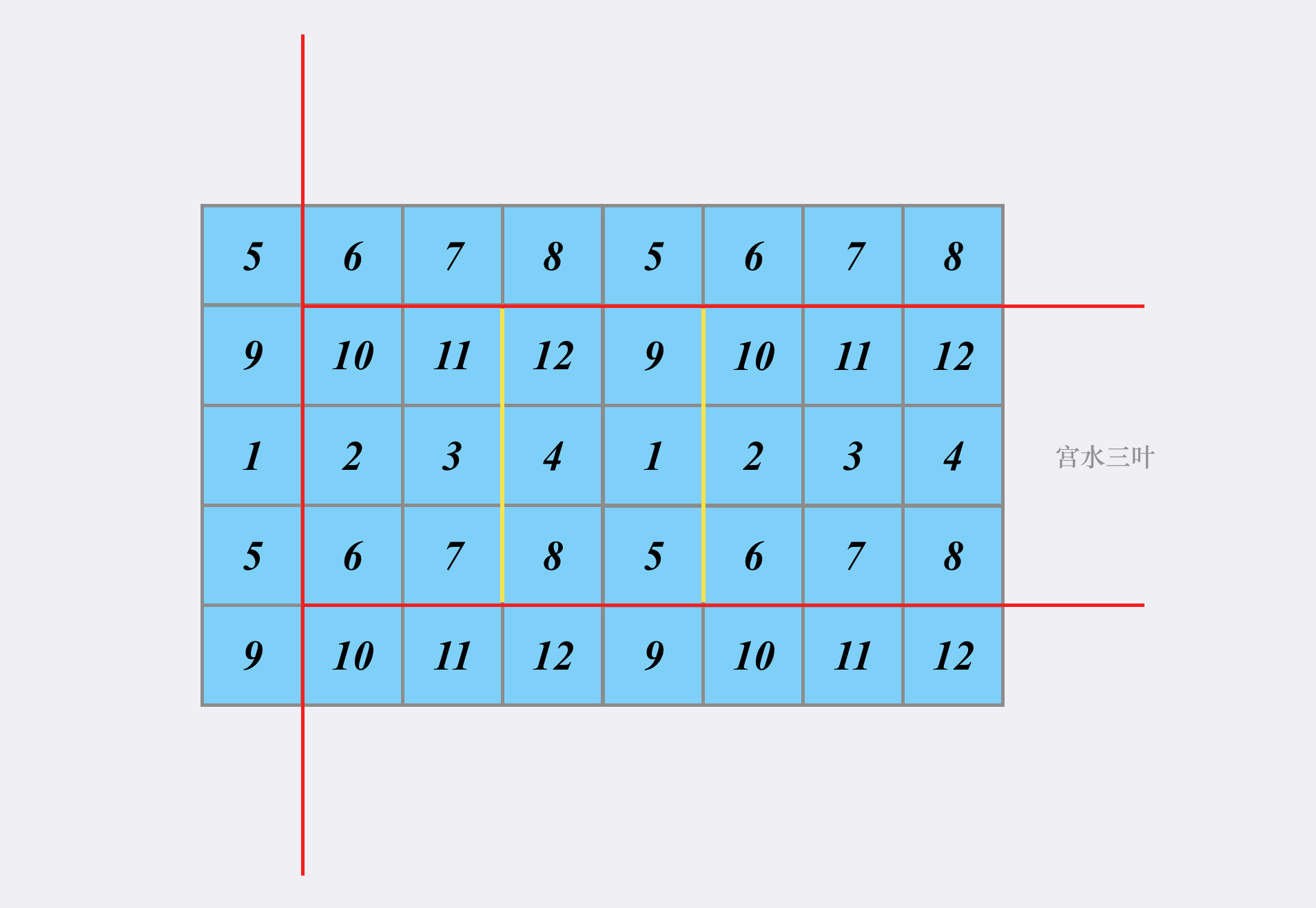
于是问题转化为「如何快速求得第四条边（黄色）的位置在哪」。

我们可以进一步将问题缩小，考虑矩阵只有一行（一维）的情况：

这时候问题进一步转化为「在一维数组中，求解和不超过 K 的最大连续子数组之和」。

如何做到这一步的？

当前原始一维数组（不是前缀和数组）中的值是该列在上下边界之间所有单元格的和

对于这个一维问题，我们可以先预处理出「前缀和」，然后枚举子数组的左端点，然后通过「二分」来求解其右端点的位置。

假定我们已经求得一维数组的前缀和数组 sum，即可得下标范围 [i,j][i,j] 的和为：
areaSum(i,j)=sum[j]−sum[i−1]⩽k

经过变形后得：
sum[j]⩽k+sum[i−1]

我们有两种思路来最大化 areaSum(i, j)：

  • 确定（枚举）左端点位置 i，求得符合条件的最大右端点 sum[j]
  • 确定（枚举）右端点位置 j，求得符合条件的最小左端点 sum[i]

对于没有负权值的一维数组，我们可以枚举左端点 i，同时利用前缀和的「单调递增」特性，通过「二分」找到符合 sum[j]⩽k+sum[i−1] 条件的最大值 sum[j]，从而求解出答案。

但是如果是含有负权值的话，前缀和将会丢失「单调递增」的特性，我们也就无法使用枚举 i 并结合「二分」查找 j 的做法。

这时候需要将过程反过来处理：我们从左到右枚举 j，并使用「有序集合」结构维护遍历过的位置，找到符合 sum[i]sum[j]−k⩽sum[i] 条件的最小值 sum[i]，从而求解出答案。

基于上述分析，解决这样的一维数组问题复杂度是O(nlogn) 的。

同时，将一维思路应用到本题（二维），复杂度要么是O(m^2 ∗nlogn) 要么是 O(n^2 * mlogm);

重点是如何与「一维」问题进行关联：显然「目标子矩阵的和」等于「子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵和」-「子矩阵左边列 与 原矩阵左边列 形成的子矩阵和」

我们可以使用 area[r] 代表「子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵和」，使用 area[l - 1] 代表「子矩阵的左边列 与 原矩阵的左边列 形成的子矩阵和」的话，则有：
target=area[r]−area[l−1]⩽k

这与我们「一维问题」完全一致，同时由「上下行」&「右边列」可以直接确定 area[r] 的大小，通过「有序集合」存储我们遍历 r 过程中的所有的 area[r] 从而实现「二分」查找符合area[r]−k⩽area[l−1] 条件的 最小 的 area[l - 1]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
var maxSumSubmatrix = function(matrix, k) {
  let ans = Number.MIN_SAFE_INTEGER;
  const m = matrix.length;
  const n = matrix[0].length;
  const sum = new Array(m + 1).fill(0).map(() => {
    return new Array(n + 1).fill(0)
  });
  // 初始化前缀和数组，sum[i][j]表示的是从（0,0）到（i - 1, j - 1）之间所有单元格的和
  for(let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
    }
  }
  // 遍历子矩阵的上边界
  for(let top = 1; top <= m; top++) {
    // 遍历子矩阵的下边界
    for(let bot = top; bot <= m; bot++) {
      // 到这里，我们就可以着手把二维矩阵问题转化为一维矩阵问题了
      // 因为上下边界的问题已经在双层循环中解决了

      // 使用有序集合维护所有遍历到的右边界
      // 也就是上下边界之间，从第0列到右边界的和
      const sumSet = new TreeSet();
      sumSet.add(0);

      for(let r = 1; r <= n; r++) {
        // 从第0列到r列，top行到bot行之间所有单元格的和。
        const right = sum[bot][r] - sum[top - 1][r];
        // 通过二分法找一个大于等于right - k的最小值
        const left = sumSet.ceiling(right - k);
        if (left !== null) {
          ans = Math.max(ans, right - left);
        }
        // 把遍历到的right加入到有序集合中，待下一次循环使用
        // 这里有一点，这个right一定是递增的，因为单元格中没有负值
        sumSet.add(right);
      }
    }
  }
  return ans;
};

空间优化

不难发现，我们在原矩阵搜索目标子矩阵的过程是严格的「从上到下」&「从左到右」的。

因此我们可以将计算前缀和的逻辑下放到搜索子矩阵的循环里去做，从而将O(m∗n) 的空间复杂度下降到O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var maxSumSubmatrix = function(matrix, k) {
  let ans = Number.MIN_SAFE_INTEGER;
  const m = matrix.length;
  const n = matrix[0].length;
  for(let i = 0; i < m; i++) { // i是行数的起点
    const sum = new Array(n).fill(0);
    for(let j = i; j < m; j++) { // j是行数的终点
      for(let c = 0; c < n; c++) {
        sum[c] += matrix[j][c]; // sum[c]指的就是从第i行到第j行之间第c列所有单元格内数据的和
      }
      const sumSet = new TreeSet();
      sumSet.add(0);
      let s = 0;
      for(const v of sum) {
        s += v;
        const ceil = sumSet.ceiling(s - k); 
        if (ceil != null) {
          ans = Math.max(ans, s - ceil);
        }
        sumSet.add(v);
      }
    }
  }
  return ans;
};

有序集合TreeSet

其实由于本题的特殊原因，每次add的都是递增的，不需要额外排序，所以add可以直接在数组中push。

而二分查找可以看我的另外一篇博客：https://sunra.top/posts/e421a043/

参考链接：

https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/solution/gong-shui-san-xie-you-hua-mei-ju-de-ji-b-dh8s/

https://leetcode-cn.com/u/ac_oier/