GAMES101 系列总结（三）：Shading

发表于 2023-04-29 更新于 2024-11-19 分类于 Unity Waline：

目前我们已经介绍了图形学中的以下几个步骤:

前三个图表示的是MVP矩阵将模型上每个点的坐标转换到屏幕空间的过程
最后一个图表示的是，将转换后的屏幕空间中的点连接成的三角面片进行光栅化的过程，即判断每个三角面片会以影响哪些像素点

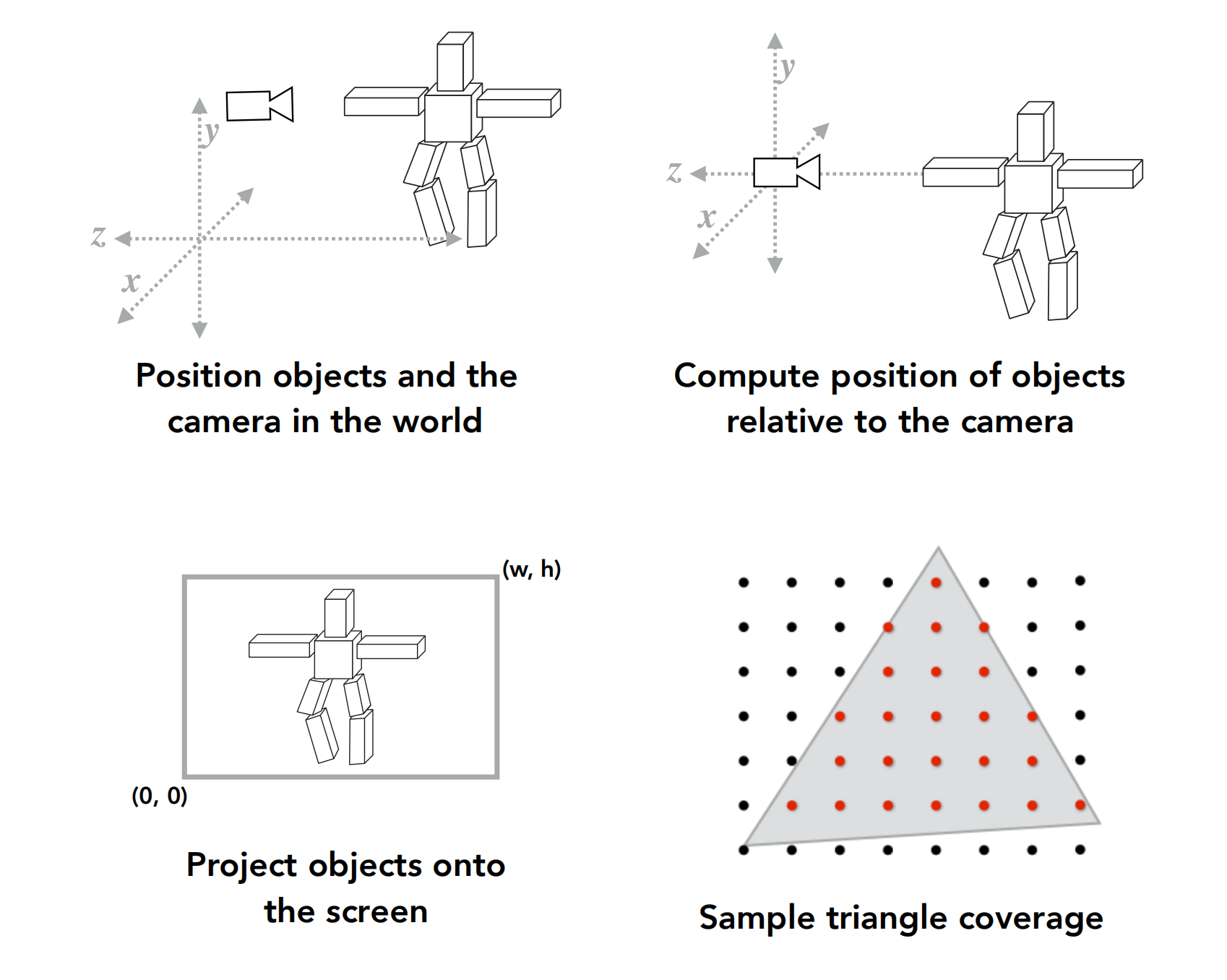
但是到目前为止，我们只是得到了每个点在屏幕空间的坐标以及它会影响到哪些像素点，但是具体影响是什么，我们还没有得到。

接下来我们说的shading的过程讲的就是如何计算这些点对像素点的影响是什么。

shading的英文翻译为：The darkening or coloring of an illustration or diagram with parallel lines or a block of color，也就是我们平时所说的阴影

但是在计算机图形学里，它指的是计算这些点对像素点的影响的过程，即这些点的颜色等。

这里我们思考一个问题，我们是如何看到日常生活中的物体的：物理的光学部分我们都了解过这个问题，我们之所以能看到一个物体，是因为物体反射出来的光进入到了我们的眼睛，反射光的颜色和角度会影响我们对这个物体的观察

所以我们在图形学中也是利用这个理论，我们shading的过程就是计算每个点的反射光的角度和颜色等。

那么我们如何利用这个理论计算着物理光照的过程呢？

首先我们需要对光照模型进行建模，也就是一个物体的光照的结果是由什么组成的。

这个建模也分为几个部分：

一个点会受到几种不同的光照影响
每种不同的光照遵循什么样的计算方式，如每种光照的颜色，角度，强度等等
不同的光照在某个点上的效果是如何叠加的
我们得到了不同的点的光照效果，如何计算出三角面中每个像素点效果，是直接三角面内的每个像素点的颜色就是三个点直接简单求平均还是怎样？
最后就是，每个点计算时的输入是什么？比如每个点的颜色，法向量是多少之类的

这里我们以一个比较简单的布林-冯模型来介绍，其他的模型可能比这个复杂，但是只是具体的算法可能不同，但是步骤还是这些步骤

一个点上有几种不同的光

在这个模型中，我们将一个物体的反射光分为三个部分：

镜面高光（Specular highlight）：出射角比较固定的反射光
漫反射（Diffuse reflection）：向各个方向反射的光
环境光（Ambient lighting）：也就是说，假设环境中没有任何光源，也不是黑的，总是有点光

注意，如果是过去使用过Unity的人，可能会接触几个概念，比如直接光和间接光，这个概念和这里的镜面反射，漫反射没关系。同时Unity中也有个概念叫做自发光，这个概念和环境光也不是一回事。

如何计算一个点上的光照效果

那么我么如何计算模型上某个点的光照效果呢？

首先是在计算一个点的光照效果的时候，我们有哪些输入：

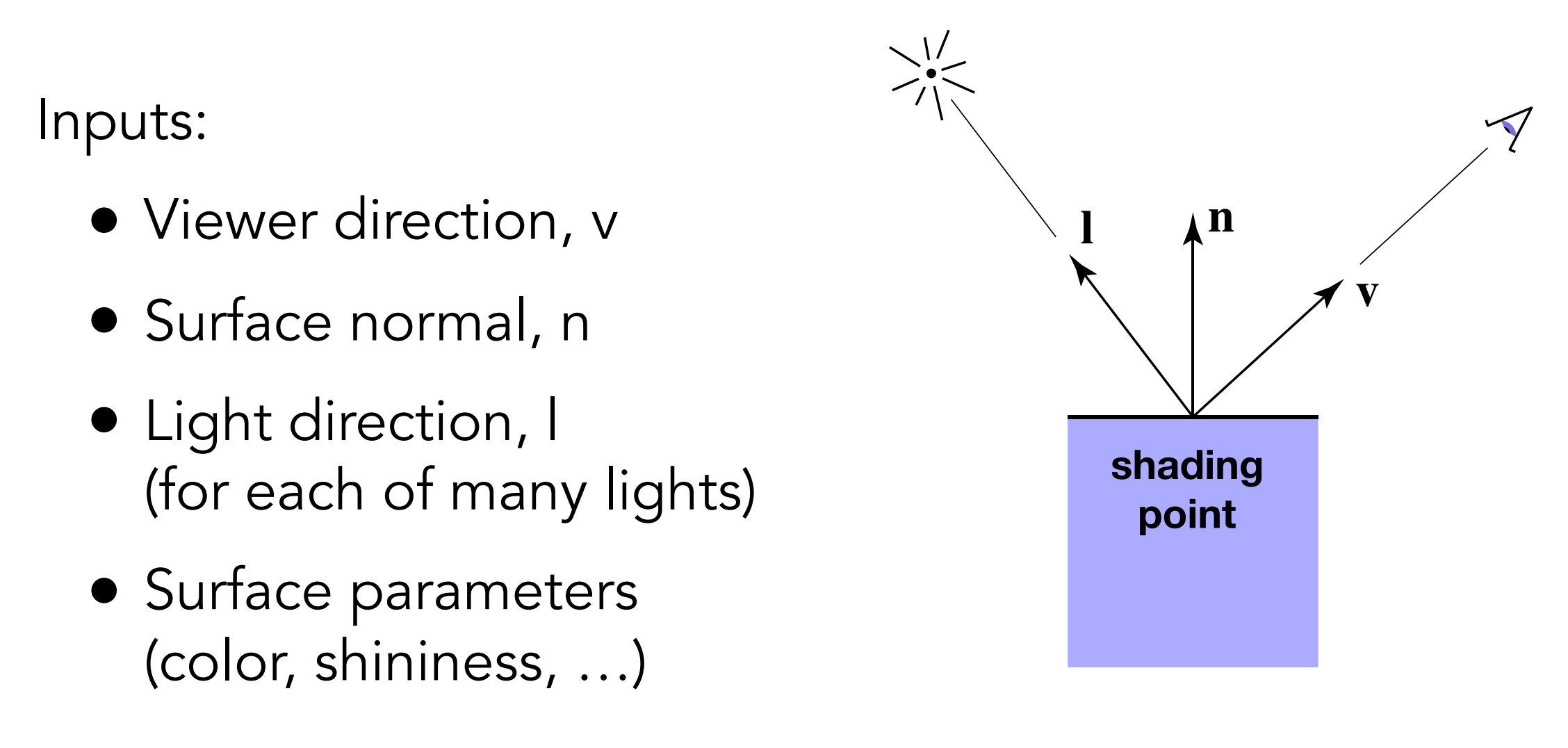
注意，上面的v向量并不是出射光的方向，而是反射点和摄像机之间的连线的方向

那么有了这些输入之后，我们要怎样计算某种光在这点的光照效果呢？

漫反射光照

所谓漫反射就是向各个角度反射的光，反射角度我们就得到了

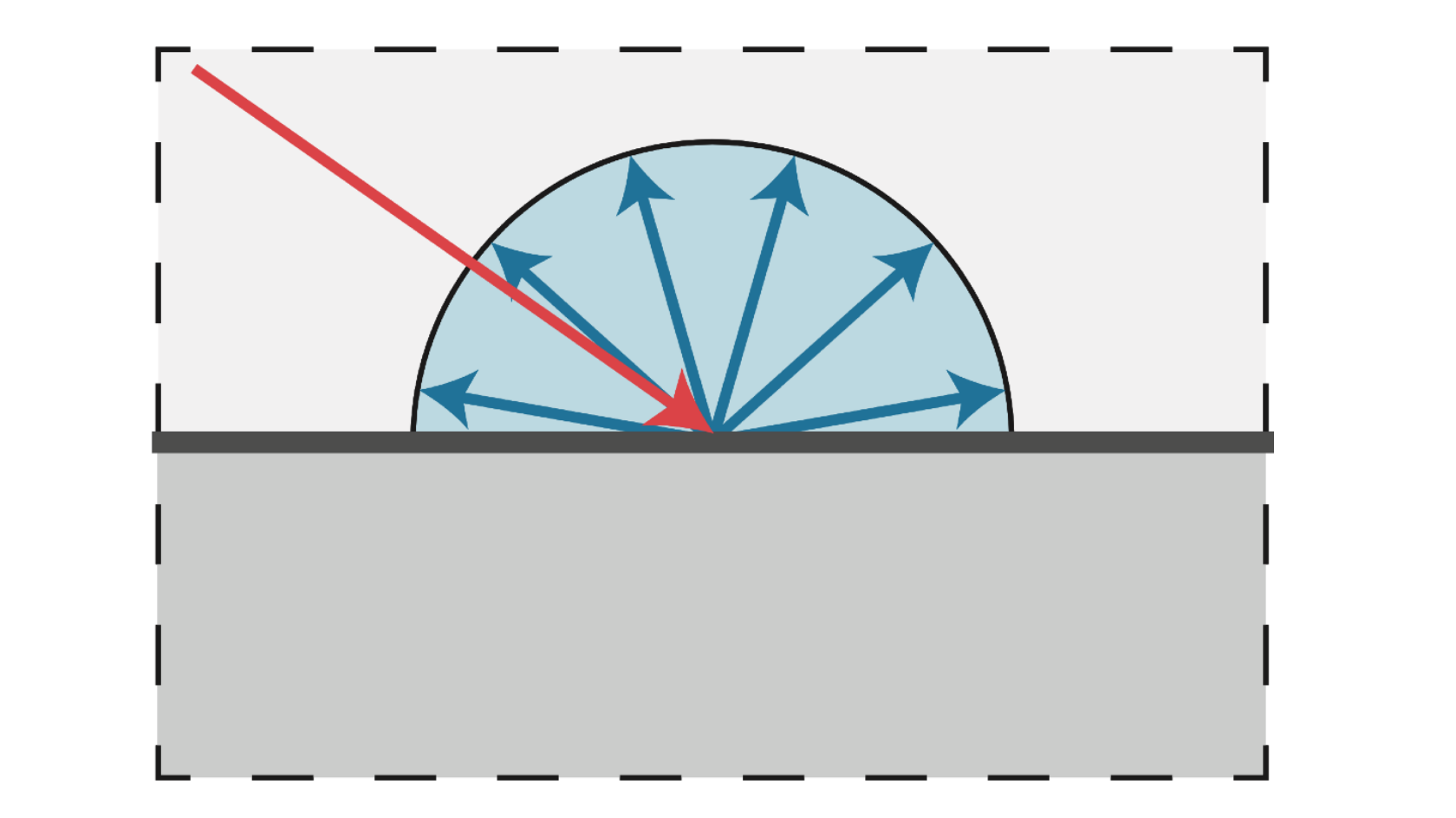
那么反射光的强度呢？也就是这个点的明暗又是怎么决定的呢？

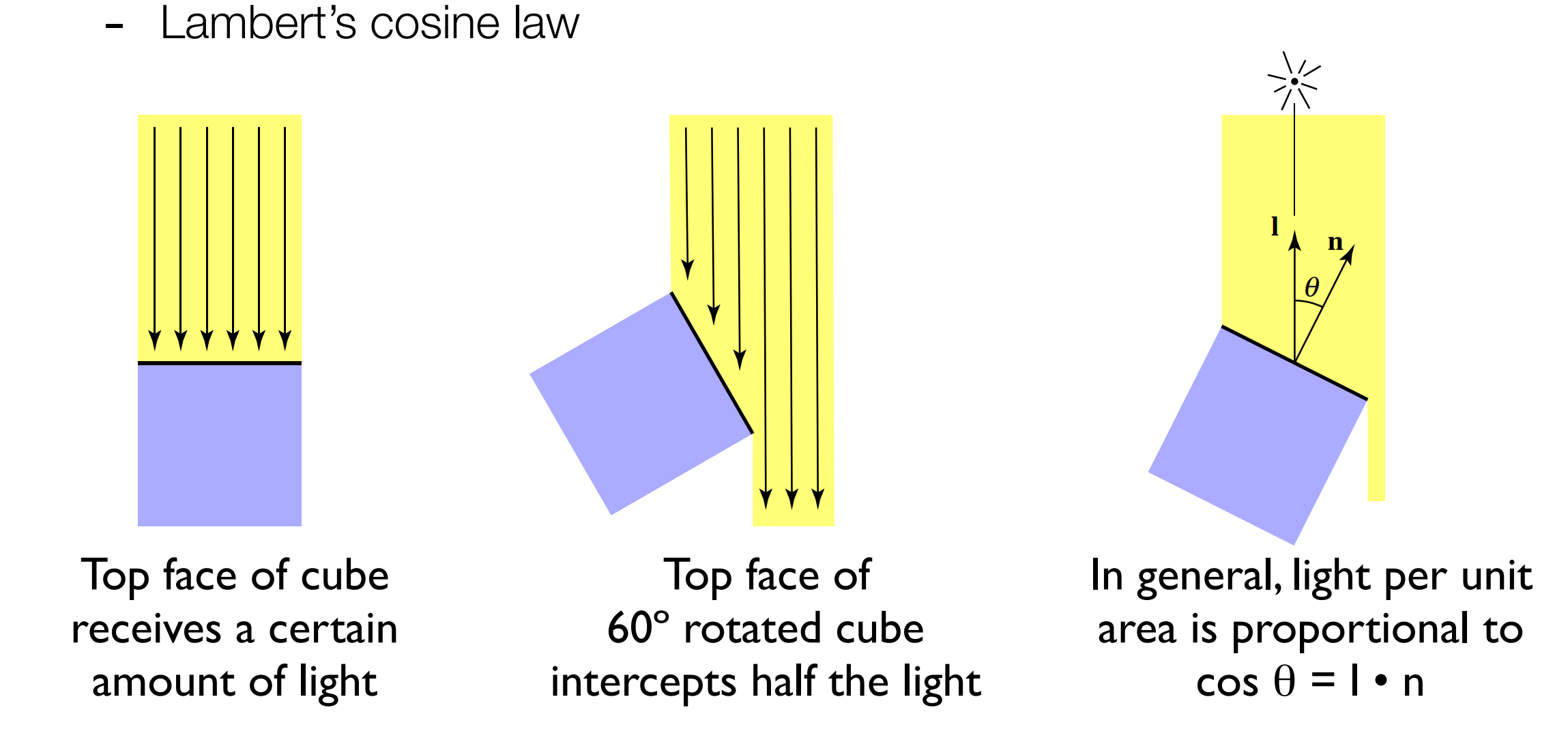
我们采取的模型是假设光照是一系列均匀密度的光线的集合，当你的平面不是和光线垂直的时候，就会有一部分光没有被反射，我们通过法线方向和入射光线的方向之间的夹角余弦来计算反射光在反射点损失了多少强度。

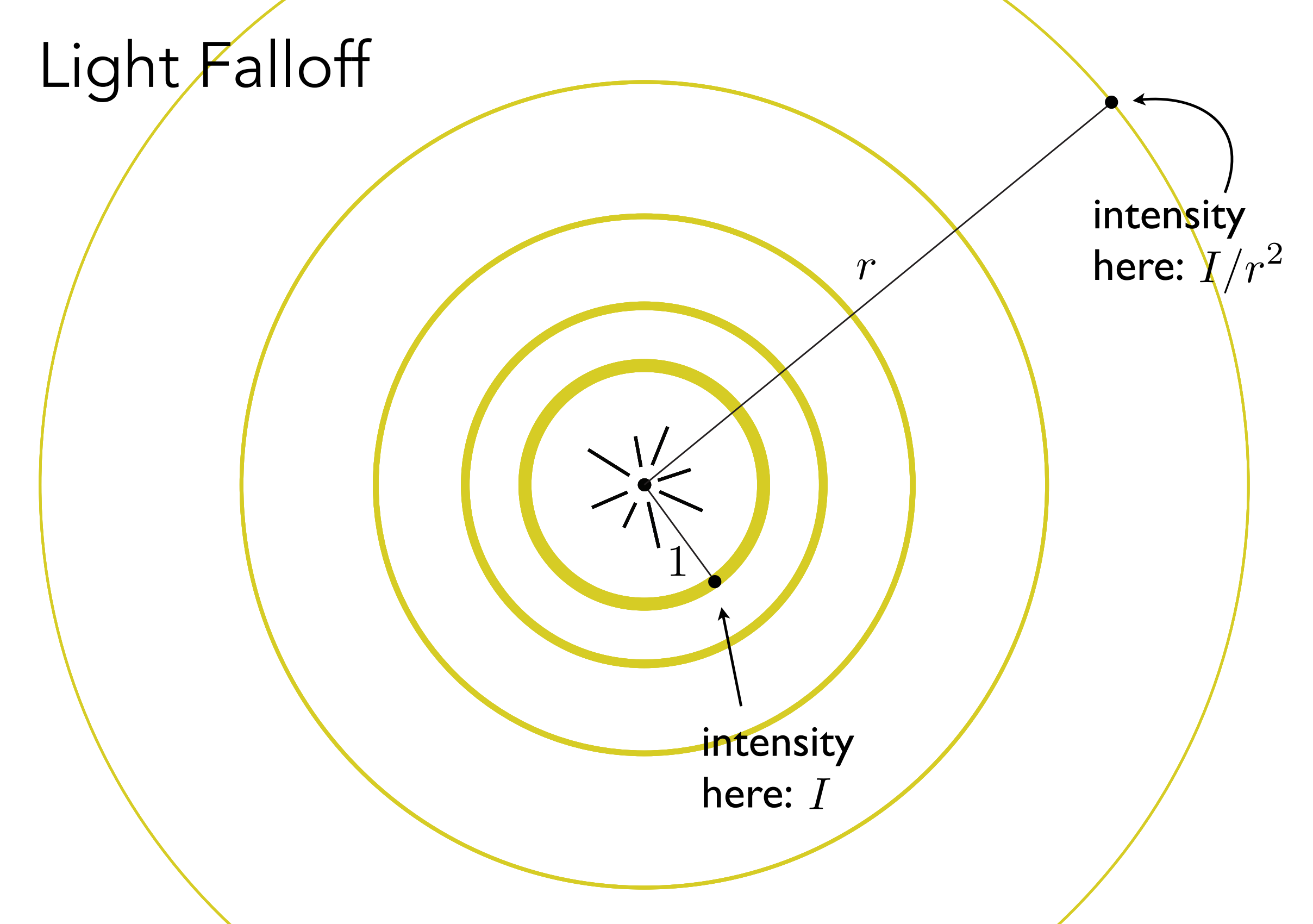
还有一个问题就是，随着距离的拉远，光照的能量也会逐渐衰减，我们也简单采用如下模型来计算，传播过程中的能量衰减

再加上这个点颜色值，我们就得到了这个点光照效果（这个颜色是怎么来的我们后面再说）

下面公式中的 $K_d$ 是漫反射系数，可以不止是这个点的颜色

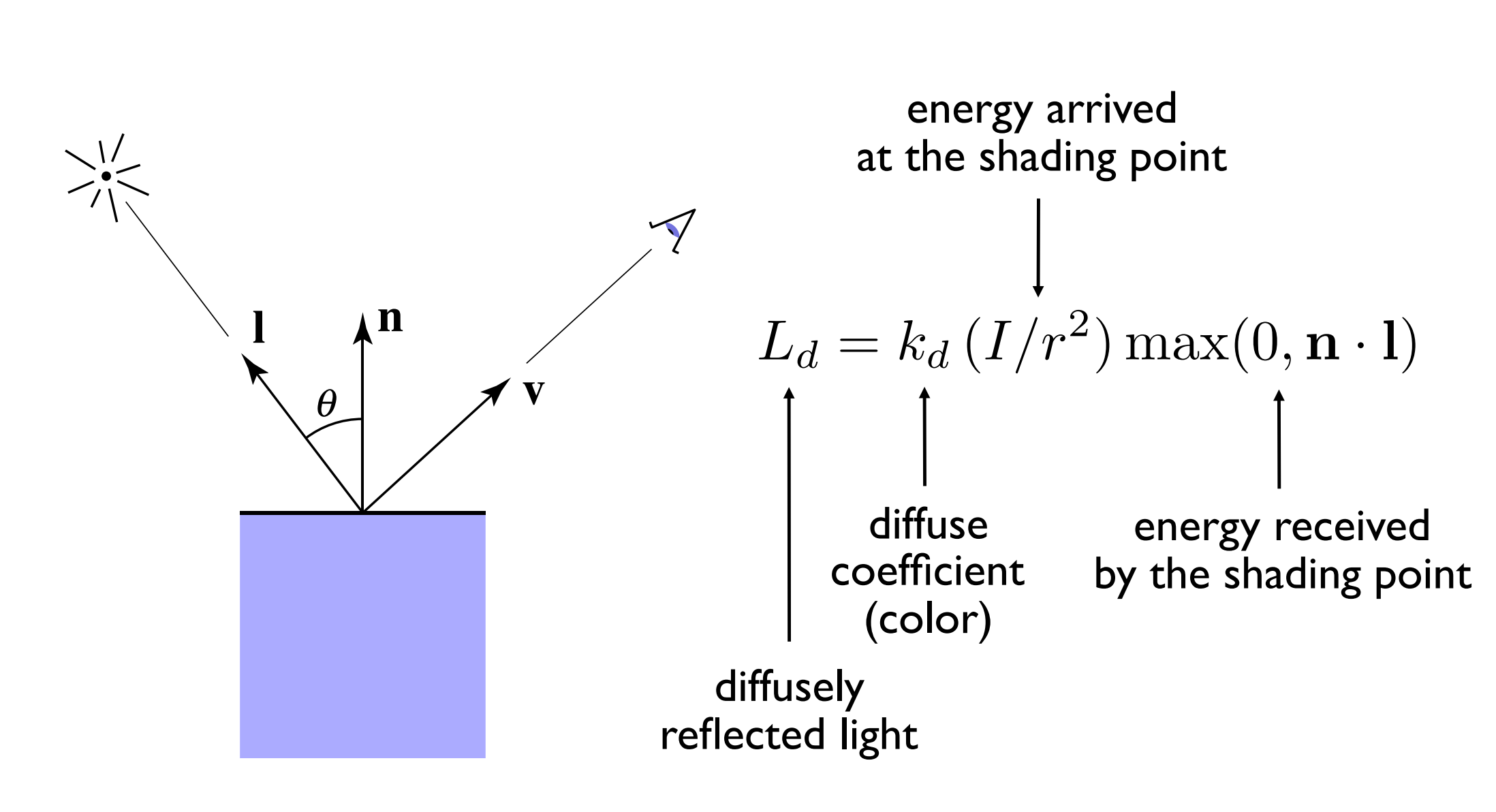
注意，真实的物理光照模型比这个复杂的多，但是模拟真实的物理光照一来理论上做不到有一个模型可以完美还原物理世界，其次就算可以，计算量过大。

高光反射

对于镜面反射来说，入射光方向与出射光方向关于法线对称，而出射光方向和观察方向约接近，高光反射鲜果愈明显

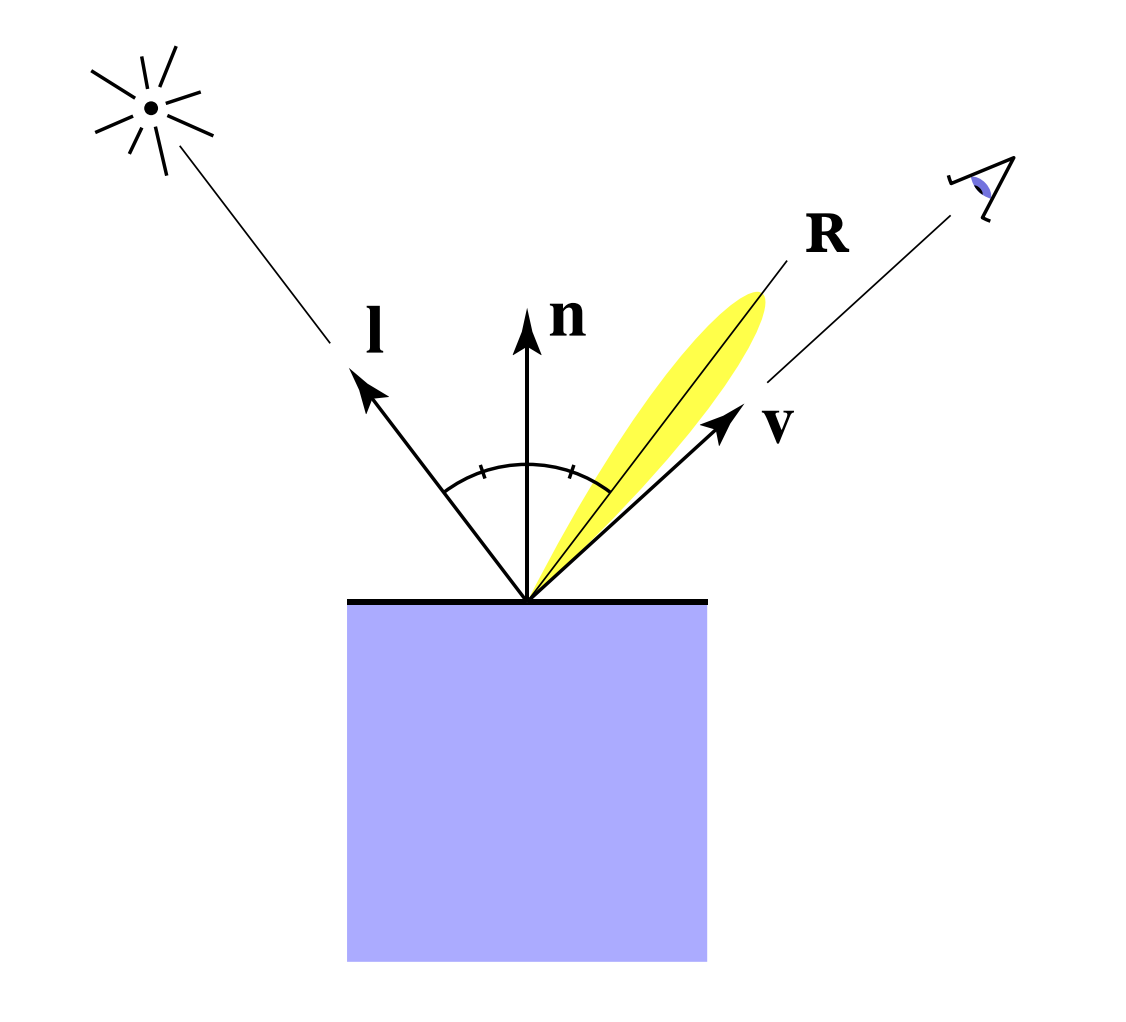
也就是说，R和V约接近，高光越明显

不过Blinn-Phong模型中采取了一种叫做半程向量的东西来计算R和V的接近程度，如下图所示：

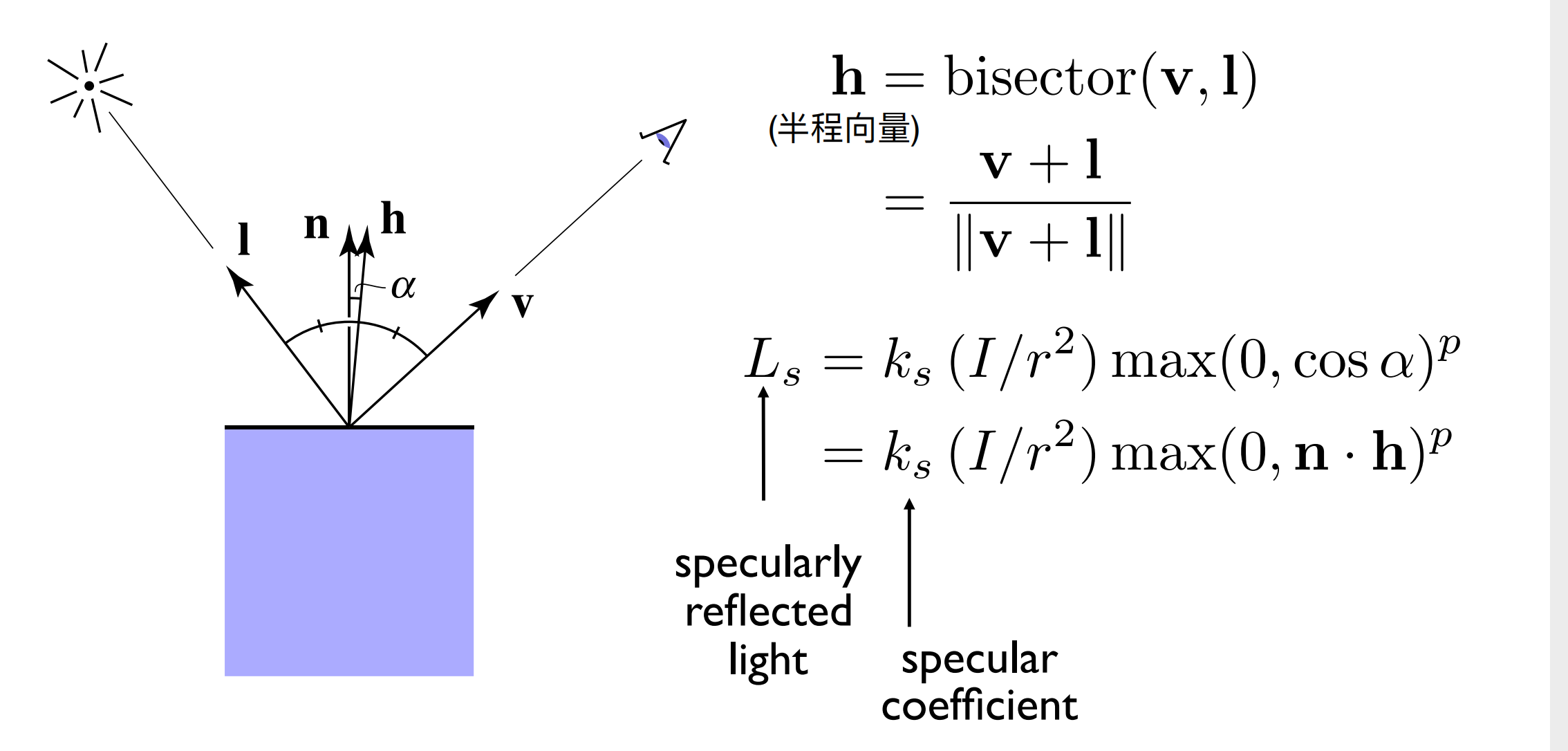
这个公式中的 $K_s$ 是高光系数，可以是这个点的颜色

我们注意到这个公式中，有个p，这个p最后会影响高光的范围：

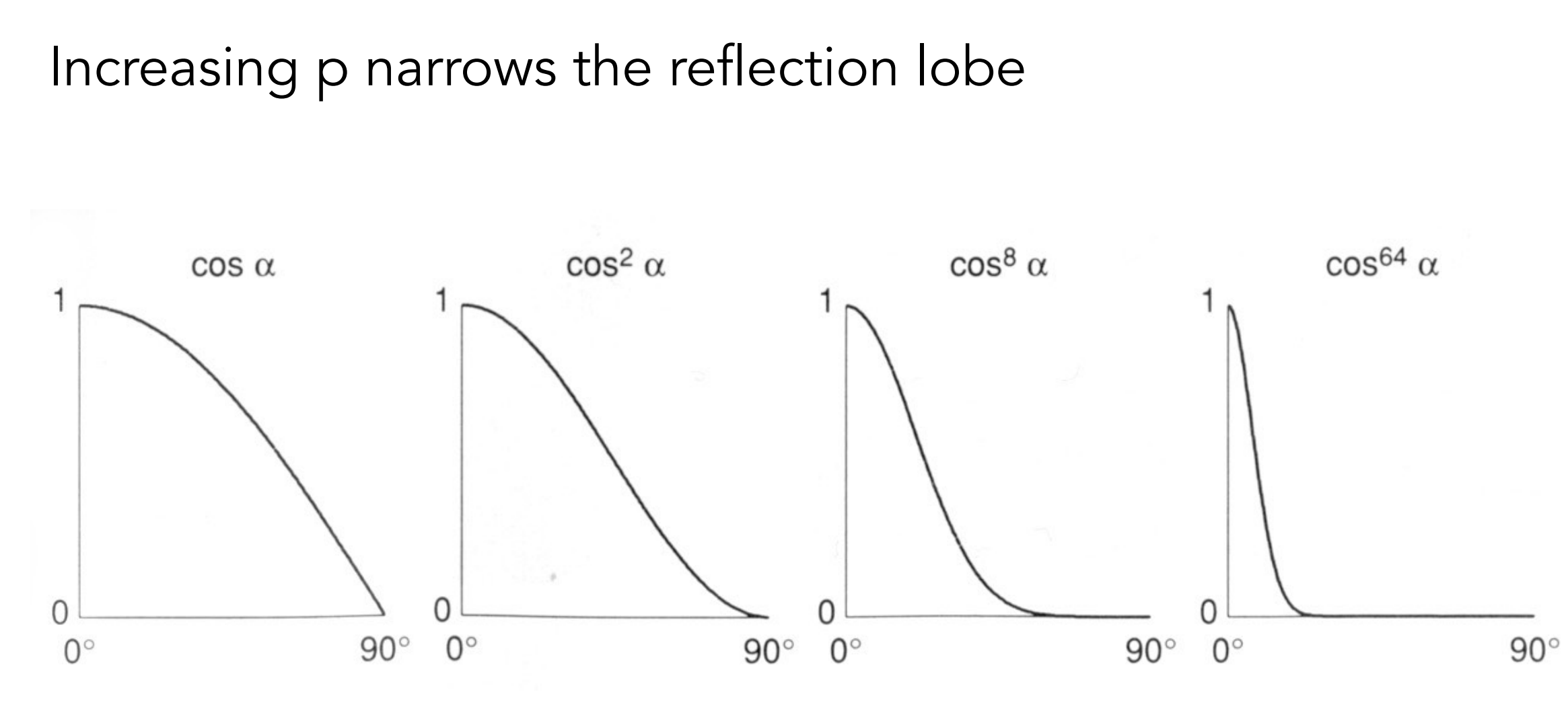
环境光

环境光我们就简单假设，每个点都还有一个固定的光就好，同样，环境光系数可以只是这点的颜色

如何叠加一个点上不同光的效果

对于Blinn-Phong模型来说，很简单，相加就好

如何根据三个点得到三角形面的光照效果

我们也有几种不同的方式计算某个面上不同像素点的效果：

Flat Shading：第一种比较简单，这个面上所有点的法向量都一样，可以通过三个点的坐标直接计算出来
Gouraud shading：利用三个点的颜色进行插值，三个点都有自己的法向量
Phong Shading：也是进行插值，不过是Phong shading是在每个像素点处计算颜色值，而不是在顶点处进行计算

Gouraud shading的插值过程是在三角形的顶点处预先计算出各个顶点的颜色值，然后在三角形内部进行插值，得到更平滑的颜色渐变效果。具体的插值过程如下：
对于每一个三角形的顶点，计算该顶点的颜色值，这可以通过给每个顶点指定颜色或者使用纹理贴图来实现。
对于三角形内部的每个像素点，计算其对应的重心坐标。重心坐标是指在三角形内部，以每个顶点为端点的三条线段的长度与该点到三条线段的距离之比。
根据每个像素点的重心坐标，计算出该像素点的颜色值。这个颜色值是通过在三个顶点的颜色值之间进行插值得到的。具体来说，对于每个像素点，我们可以用重心坐标来计算出三个顶点的权重，然后将三个顶点的颜色值按照权重进行加权平均即可得到该像素点的颜色值。
通过这样的插值过程，我们可以得到一个平滑的颜色渐变效果，使得三角形表面的颜色变化更加自然。
Gouraud shading是在三角形的顶点处计算颜色值，然后在三角形内进行插值得到平滑的颜色渐变效果。这种方法的优点是计算速度快，适合实时渲染，但缺点是在插值过程中可能出现颜色不连续的情况，而且不能完全准确地呈现物体表面的光照效果。
Phong shading是在每个像素点处计算颜色值，而不是在顶点处进行计算。这个方法通过在每个像素点处计算出法向量来模拟光照效果。然后使用法向量和光照方向之间的夹角来计算每个像素点的颜色值。这种方法的优点是可以准确地模拟物体表面的光照效果，但缺点是计算量大，速度较慢，不适合实时渲染。

下图展示的是随着面数增多，三种不同方式下的效果

关于每个点的法向量是怎么来的，也有不同的方式，比如对于一个球体，法线方向就是球心和球面上某个点的连线的方向。而对于普通的几何体，我们可以计算某个点在哪几个不同的面上，分别计算出每个面的法向量之后去个平均即可。方式有很多，选择合适的就好

Texture

目前为止我们已经讲了MVP矩阵，三角形化，光栅化，光照计算等。我们还差最后一个环节，即之前我们说的都是计算过程，这个过程的输入来源我们还没有讲。

不过在讲这个之前，我们先把之前的知识串起来，然后看一下我们在何时获取并使用这些输入。

把这些知识串联起来的内容就叫做渲染管线，其实我之前的博客有讲过，这里就不细说了，可以看我之前的博客Unity渲染流水线（一）从模型上的点到屏幕上的点：

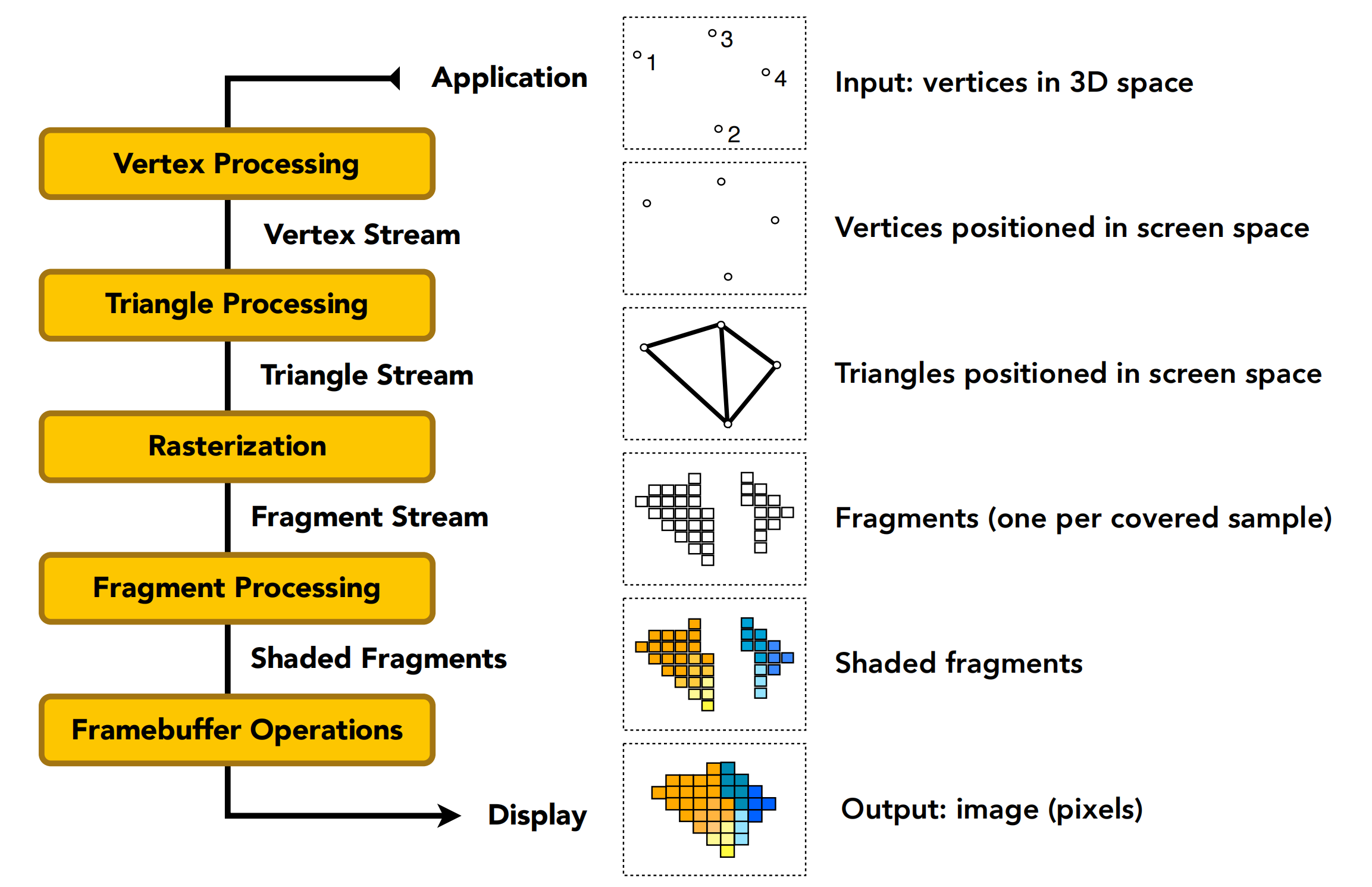
在这个渲染管线中，我们能够进行自定义编程的是，第一步和第四步，分别对应的是顶点着色器和片元着色器。像是三角形化和光栅化，虽然我们之前费过一些时间去理解它的原理，会遇到什么问题，如何优化，但是其实这个过程是Hardcode在GPU当中的。

在这个计算过程中，最终的点会变成不同的颜色，是由输入决定的，我们可以为每个点设置自己的属性，包括这个点的颜色，法线方向等等，而输入的方式就是通过Texture，即贴图不仅仅可以用来控制每个点的颜色，也可以用来控制任意一种点的属性。

具体的应用方式就是，模型的每个点出了自身的位置坐标外还可以有几套UV坐标，这是一个二维坐标，表明的是这个点的某个属性在贴图上的坐标对应的属性。举个例子，某个点的颜色的UV坐标是（0.5，0.5）,那么这个点的颜色就是对应贴图上（0.5，0.5）点的颜色。

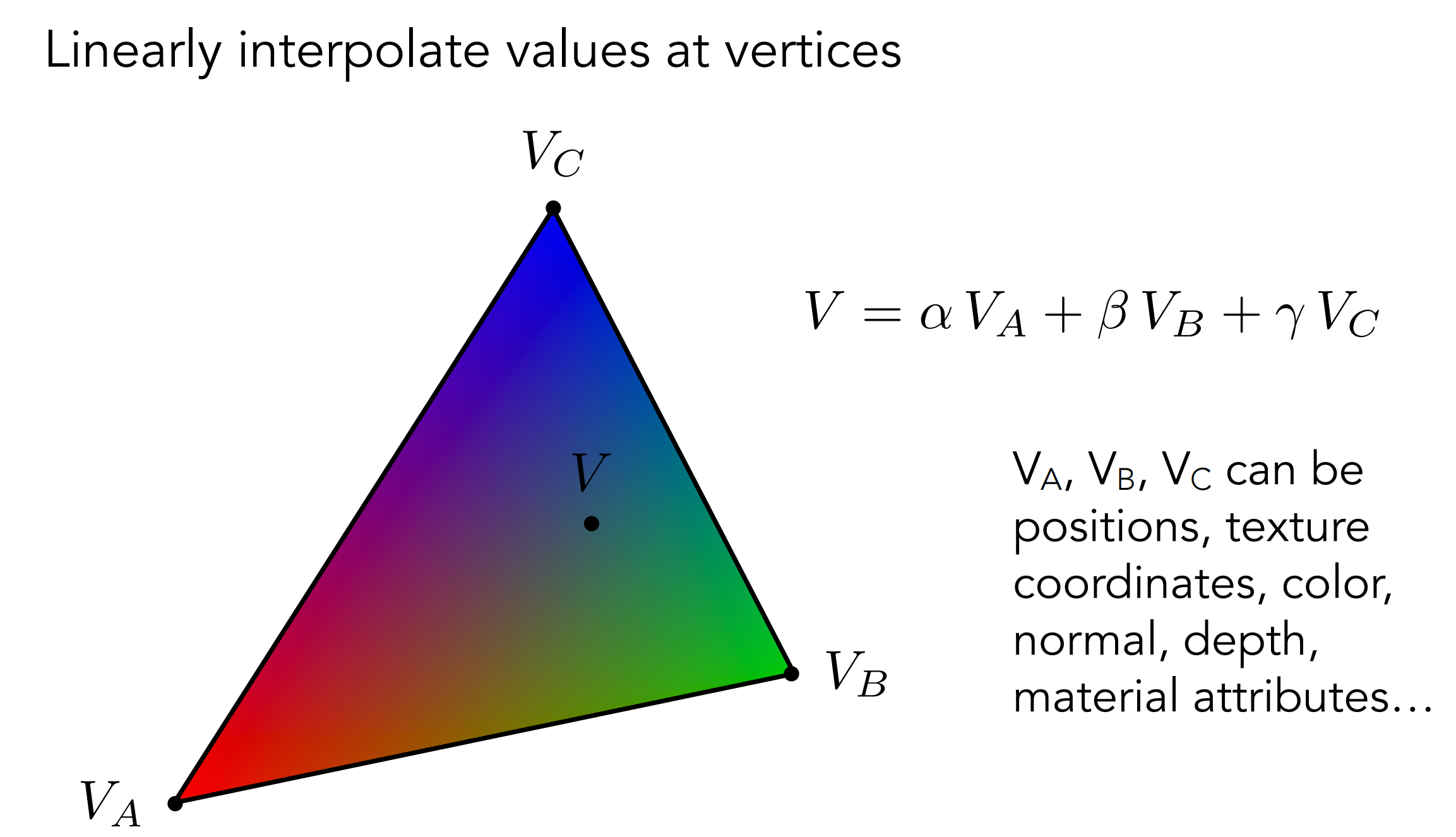
但现在的问题是，我们只能针对某个点设置属性，对于一个三角面片，我们如何计算其中某个点的属性值呢？我们以Gouraud Shading来说明，这里牵扯到一个东西叫做重心坐标。

所谓的重心坐标就是一套三角形内部的坐标系，对于一个确定的三角形，其内部的任意一个点都可以用这个坐标系来表示

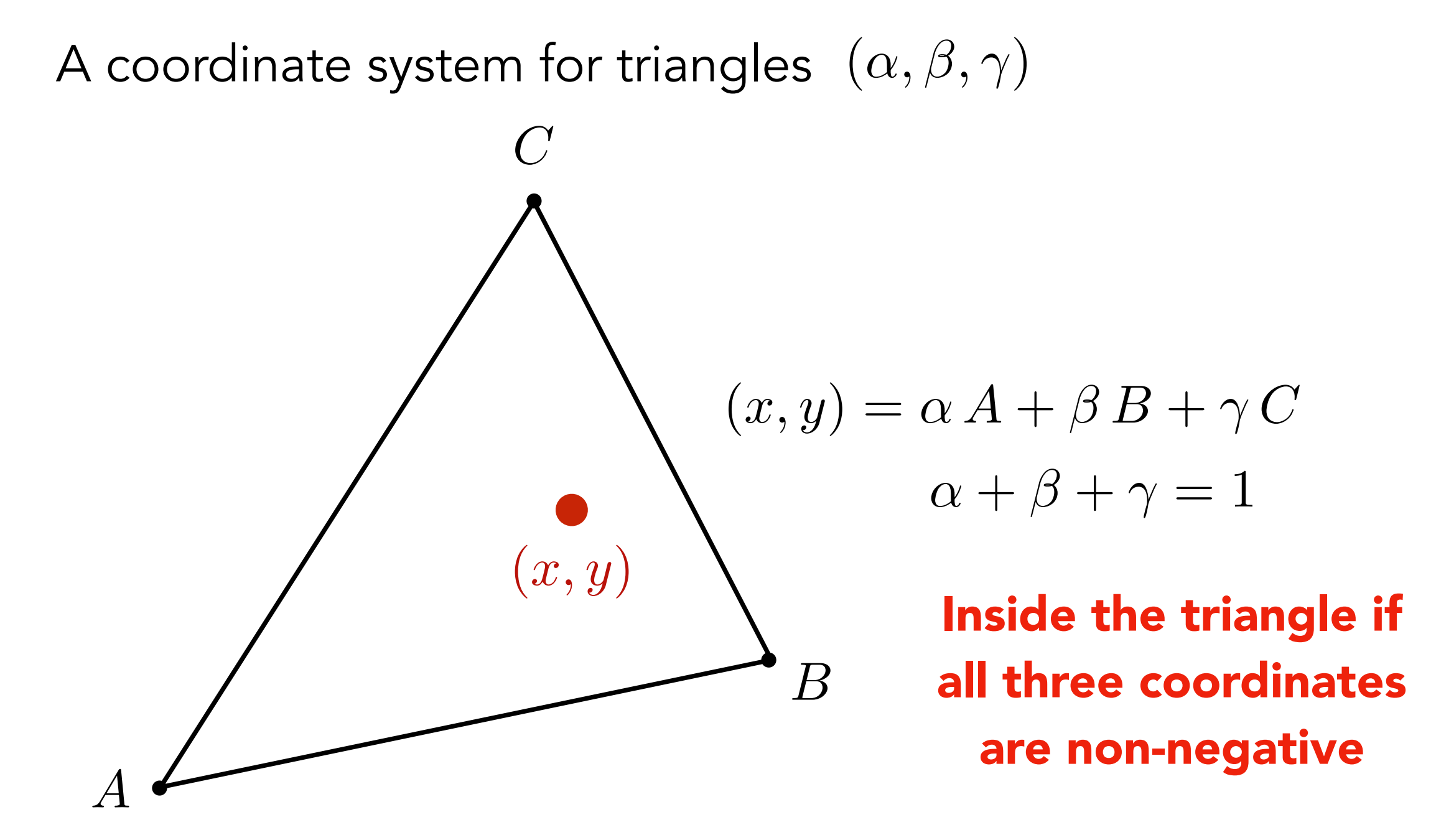
那么这套坐标系有什么用呢？如下所示：

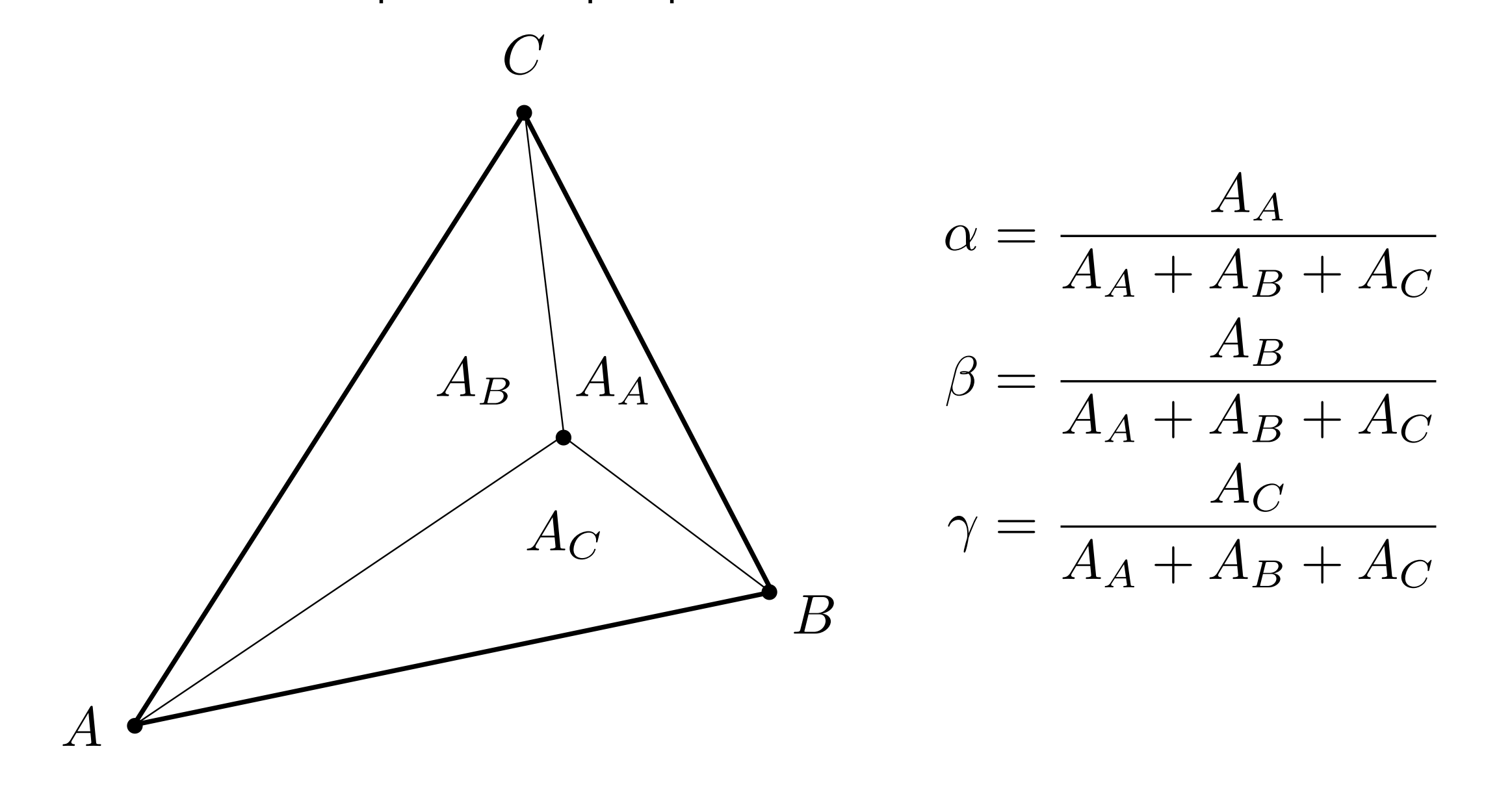
它能表示内部分成的三个三角形的面积比，这样我们就可以利用重心坐标计算任意一个点的插值过程中，三个顶点对于当前点的影响了：