卡特兰数的等价问题

发表于 更新于 分类于 Waline：

之前的一篇关于机器智能的本质就是分类和组合的博客，我们提到过，很多应用科学将实际问题变成了信息处理的分类，组织，查找和重组，而计算机的算法再把这些信息处理问题变为计算问题。显然，这里有两个桥梁，通过第一个桥梁，很多问题其实到了算法这一步都是等价的，这次我们就用卡特兰数来说明这个问题。

几个具体的问题

下面我们列举几个问题，大家可以先思考一下他们是怎么解决，当然我们放在这里。说明他们其实都是卡特兰数的问题，在这个基础上，大家试试能不能看出来如何解决。

进出栈序列

这是一道最经典的入门级卡特兰数题目，如果能把这题看懂，相信后面的题目也能迎刃而解。

题目描述：

n 个元素进栈序列为：1，2，3，4，…，n，则有多少种出栈序列

括号序列

题目描述：

n 对括号，则有多少种 “括号匹配” 的括号序列

满二叉树

题目描述

n + 1 个叶子节点能够构成多少种形状不同的（国际）满二叉树

（国际）满二叉树定义：如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是满二叉树。

电影购票

题目描述

电影票一张 50 coin，且售票厅没有 coin。m 个人各自持有 50 coin，n 个人各自持有 100 coin。

则有多少种排队方式，可以让每个人都买到电影票。

走格子

在一个w×h的网格上，你最开始在(0,0)上，你每个单位时间可以向上走一格，或者向右走一格，在任意一个时刻，你往右走的次数都不能少于往上走的次数，问走到(n,n),0≤n有多少种不同的合法路径。

什么是卡特兰数

介绍

学卡特兰数我觉得可能比组合数要难一点，因为组合数可以很明确的告诉你那个公式是在干什么，而卡特兰数却像是在用大量例子来解释什么时卡特兰数

这里，我对卡特兰数做一点自己的理解

卡特兰数是一个在组合数学里经常出现的一个数列，它并没有一个具体的意义，却是一个十分常见的数学规律

对卡特兰数的初步理解：有一些操作，这些操作有着一定的限制，如一种操作数不能超过另外一种操作数，或者两种操作不能有交集等，这些操作的合法操作顺序的数量

为了区分组合数，这里用fn表示卡特兰数的第n项

从零开始，卡特兰数的前几项为1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,35357670,129644790…

定义

递归定义

fn=f0∗fn−1+f1∗fn−2+…+fn−1f0，其中n≥2f_n=f_0∗f_{n−1}+f_1∗f_{n−2}+…+f_{n−1}f_0，其中n≥2

递推关系

fn=4n−2n+1fn−1fn=\frac{4n - 2}{n + 1}f_{n−1}

通项公式

fn=1n+1C2nn+1fn=\frac{1}{n + 1}C_{2n}^{n+1}

经化简后可得

fn=C2nn−C2nn+1=C2nn−C2nn−1fn=C_{2n}^n - C_{2n}^{n+1} = C_{2n}^n - C_{2n}^{n-1}

只要我们在解决问题时得到了上面的一个关系，那么你就已经解决了这个问题，因为他们都是卡特兰数列

建立具体问题于卡特兰数之间的桥梁

走格子

我们先以最后一个问题为例子来讲

直接求不好，考虑求有多少种不合法路径
路径总数为在2n次移动中选n次向上移动，即C2nnC_{2n}^n

画一下图，我们把y=x+1这条线画出来，发现所有的合法路径都是不能碰到这条线的，碰到即说明是一条不合法路径

先随便画一条碰到这条线的不合法路径，所有的不合法路径都会与这条线有至少一个交点，我们把第一个交点设为(a,a+1)

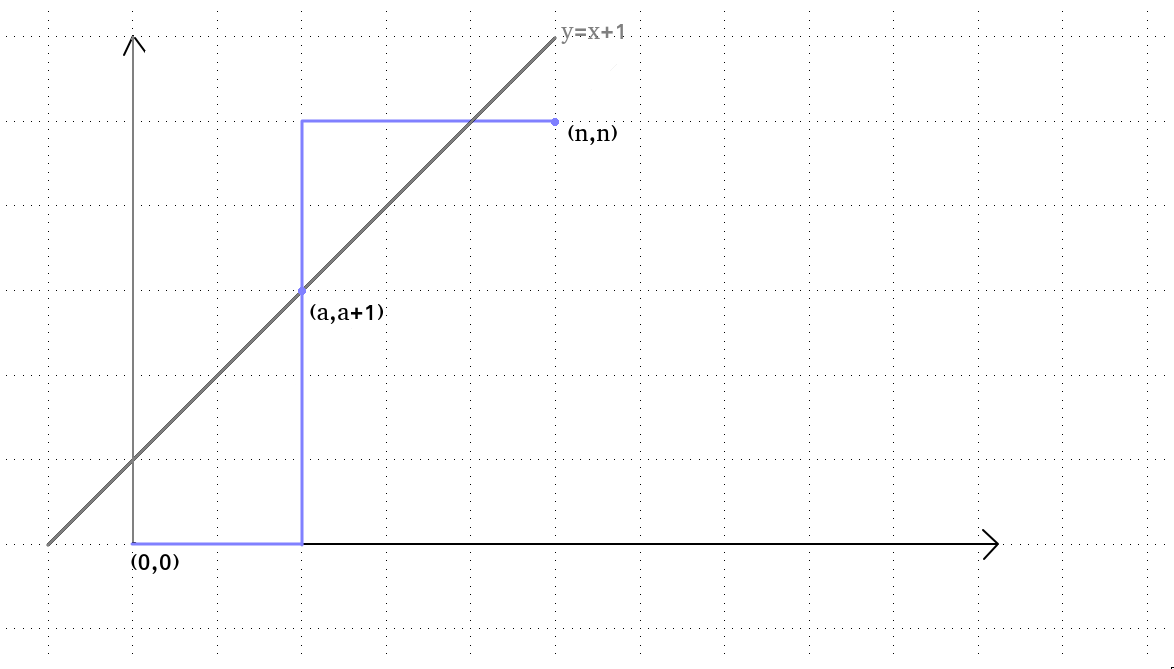
我们把(a,a+1)之后的路径全部按照y=x+1这条线对称过去这样，最后的终点就会变成(n−1,n+1)

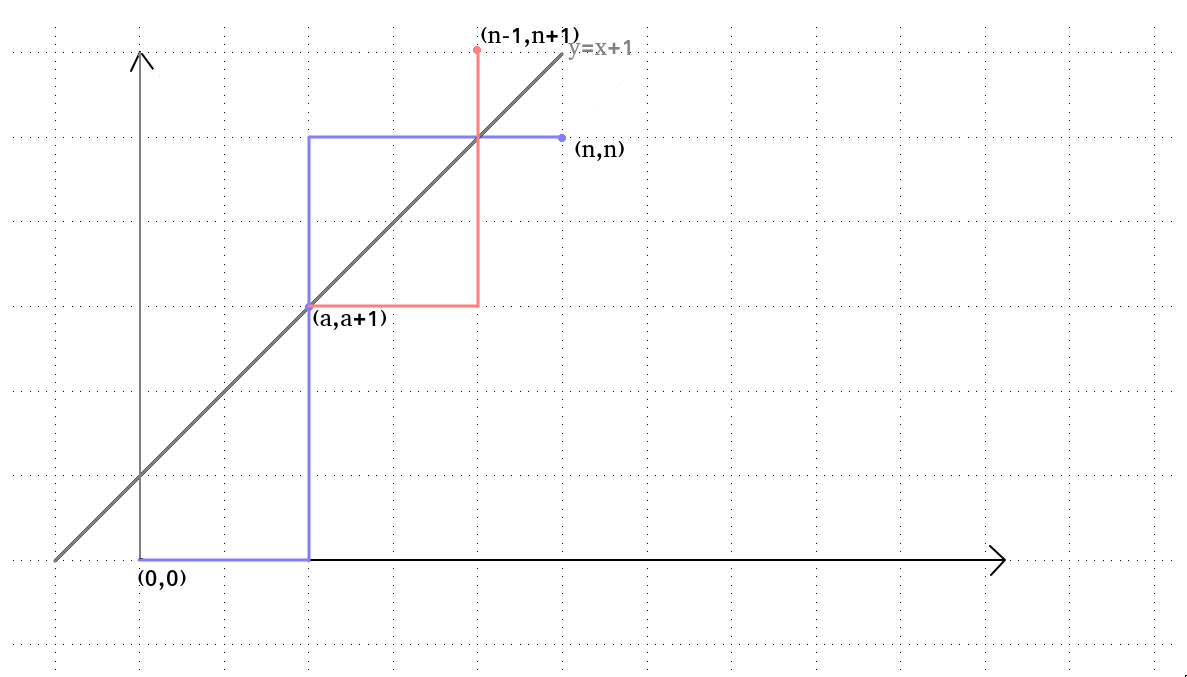
由于所有的不合法路径一定会与y=x+1有这么一个交点

我们可以得出，所有不合法路径对称后都唯一对应着一条到(n−1,n+1)的路径且所有到(n−1,n+1)的一条路径都唯一对应着一条不合法路径（只需将其对称回去即可）

所以不合法路径总数是C2nn−1C^{n−1}_{2n}

那么合法的路径总数为C2nn−C2nn−1C^n_{2n}−C^{n−1}_{2n}

这是一个非常好用且重要的一个方法，其它的问题也可以用该方法解决

即找到不合法路径唯一对应的到另一个点的路径

此时我们再回头看一开始我们提出的几个问题：

括号序列

你有n个左括号，n个右括号，问有多少个长度为2n的括号序列使得所有的括号都是合法的

合法的序列个数为卡特兰数

要使所有的括号合法，实际上就是在每一个前缀中左括号的数量都不少于右括号的数量将左括号看做1，右括号看做0，这题又和上面那题一模一样了

进出栈序列

有一个栈，我们有2n次操作，n次进栈，n次出栈，问有多少中合法的进出栈序列

合法的序列个数为卡特兰数

要使序列合法，在任何一个前缀中进栈次数都不能少于出栈次数…

后面就不用我说了吧，和上面的问题又是一模一样的了

满二叉树

使用深度优先搜索这个满二叉树，向左扩展时标记为 +1，向右扩展时标记为 -1。

由于每个非叶子节点都有两个左右子节点，所有它必然会先向左扩展，再向右扩展。总体下来，左右扩展将会形成匹配，即变成进出栈的题型。n + 1 个叶子结点会有 2n 次扩展，构成 卡特兰数 种形状不同的满二叉树。

总结

基本上所有的卡特兰数问题经过一定的转换都可以还原成进出栈问题。因此，只要我们能够学会进出栈问题的解法，无论问题再怎么变化，本质还是不变的。

卡特兰数问题中都会存在一种匹配关系，如进出栈匹配，括号匹配等，一旦计数问题中存在这种关系，那我们就需要去考虑这是否是卡特兰数问题。此外，我们还可以记住序列前四项：1, 1, 2, 5，这些将有利于我们联想到卡特兰数。