最短路径算法

发表于 更新于 分类于 Waline：

上周的博客中我们讨论并实现了图的拓扑排序，这周我们继续学习图的另外一种基础的算法，最短路径算法Dijkstra算法，以及如何将其改造成我们平时导航或者游戏中经常使用中用到的寻路算法。

优先级队列（堆）

由于Dijkstra算法中需要用到优先级队列，所以我们先模仿实现一个，采用堆的形式.

首先解释下堆是什么：

  • 堆是一个完全二叉树；

  • 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

如何实现一个堆

要实现一个堆，我们先要知道，堆都支持哪些操作以及如何存储一个堆。

我们都知道，完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点，这一点也是我们要用堆来实现优先级队列的一点原因。

如何插入元素

往堆中插入一个元素后，我们需要继续满足堆的两个特性。

如果我们把新插入的元素放到堆的最后，你可以看我画的这个图，是不是不符合堆的特性了？于是，我们就需要进行调整，让其重新满足堆的特性，这个过程我们起了一个名字，就叫做堆化（heapify）。

堆化实际上有两种，从下往上和从上往下。这里我先讲从下往上的堆化方法。

我们可以让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系，我们就互换两个节点。一直重复这个过程，直到父子节点之间满足刚说的那种大小关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Heap {
    constructor(capacity) {
        this.n = capacity;
        this.a = new Array(capacity);
        this.count = 0;
    }

    swap(i, j) {
        const temp = this.a[i];
        this.a[i] = this.a[j];
        this.a[j] = temp;
    }

    add(data) {
        if (this.count >= this.n) {
            return;
        }
        this.count++;
        this.a[this.count] = data;
        let i = this.count;
        while(Math.floor(i / 2) > 0 && this.a[i] < this.a[Math.floor(i / 2)]) {
            this.swap(i, Math.floor(i / 2));
            i = Math.floor(i / 2);
        }
    }
}

删除堆顶元素

从堆的定义的第二条中，任何节点的值都大于等于（或小于等于）子树节点的值，我们可以发现，堆顶元素存储的就是堆中数据的最大值或者最小值。假设我们构造的是大顶堆，堆顶元素就是最大的元素。

当我们删除堆顶元素之后，就需要把第二大的元素放到堆顶，那第二大元素肯定会出现在左右子节点中。然后我们再迭代地删除第二大节点，以此类推，直到叶子节点被删除。

但是上述方法容易破坏掉堆的结构

实际上，我们稍微改变一下思路，就可以解决这个问题。你看我画的下面这幅图。我们把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Heap {
    constructor(capacity) {
        this.n = capacity;
        this.a = new Array(capacity);
        this.count = 0;
    }

    swap(i, j) {
        const temp = this.a[i];
        this.a[i] = this.a[j];
        this.a[j] = temp;
    }

    add(data) {
        if (this.count >= this.n) {
            return;
        }
        this.count++;
        this.a[this.count] = data;
        let i = this.count;
        while(Math.floor(i / 2) > 0 && this.a[i] < this.a[Math.floor(i / 2)]) {
            this.swap(i, Math.floor(i / 2));
            i = Math.floor(i / 2)
        }
    }

    update(data) {
        for(let i = 0; i < this.count; i++) {
            if (this.a[i].key === data.key) {
                this.a[i] = data;
                break;
            }
        }
    }

    poll() {
        if(this.count === 0) {
            return -1;
        }
        this.a[0] = this.a[this.count];
        this.count--;
        this.heapify();
    }

    heapify() {
        let i = 0;
        while(true) {
            let maxPos = i;
            if (i * 2 <= this.count && this.a[i] > this.a[i * 2]) {
                maxPos = i * 2;
            }
            if (i * 2 + 1 <= this.count && this.a[i] > this.a[i * 2 + 1]) {
                maxPos = i * 2 + 1;
            }
            if (maxPos === i) {
                break;
            }
            this.swap(i, maxPos);
            i = maxPos;
        }
    }
}

Dijkstra算法

首先来一张算法的步骤图

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Graph {
    constructor(v) {
        this.v = v;
        this.adj = new Array(v).fill([]);
    }

    addEdge(s, t, w) {
        this.adj[s].push(new Edge(s, t, w));
    }

    dijkstra(s, t) {
        let predecessor = new Array(this.v);
        let vertexes = new Array(this.v);
        for(let i = 0; i < this.v; i++) {
            vertexes[i] = new Vertex(i, Number.MAX_SAFE_INTEGER);
        }
        let queue = new Heap(this.v);
        let inqueue = new Array(this.v).fill(false);
        vertexes[s].dist = 0;
        queue.add(vertexes[s]);
        inqueue[s] = true;
        while(!queue.isEmpty()) {
            const minVertex = queue.poll();
            if (minVertex.id === t) {
                break;
            }
            for(let i = 0; i < this.adj[minVertex.id].length; i++) {
                const edge = this.adj[minVertex.id][i];
                const nexeVertex = vertexes[edge.tid];
                if (minVertex.dist + edge.w < nexeVertex.dist) {
                    nexeVertex.dist = minVertex.dist + edge.w;
                    predecessor[nexeVertex.id] = minVertex.id;
                    if (inqueue[nexeVertex.id]) {
                        queue.update(nexeVertex);
                    } else {
                        queue.add(nexeVertex);
                        inqueue[nexeVertex.id] = true;
                    }
                }
            }
        }
        console.log(s);
        print(s, t, predecessor);

    }

    print(s, t, predecessor) {
        if (s === t) {
            return;
        }
        print(s, predecessor[t], predecessor);
        console.log(`->${t}`);
    }
}
class Edge {
    constructor(sid, tid, weight) {
        this.sid = sid;
        this.tid = tid;
        this.w = weight;
    }
}

class Vertex {
    constructor(id, dist) {
        this.id = id;
        this.dist = dist;
    }
}

dijkstra算法的思路有点像BFS，从起始顶点开始遍历它所能到的所有顶点，然后依次更新到这些顶点的最短路径，更新完之后加入到优先级队列中，接下来从优先级队列中拿出当前dist最小的顶点，然后计算出它所能到的所有顶点，依次更新，然后不断重复上述过程。

但其实也不是完全的BFS，因为优先级队列与普通队列不同，它会在每次插入数据时调整数据的位置，保证头部的数据是队列中的最小值，并不是先进先出。

A*算法（简化Dijkstra算法）

魔兽世界、仙剑奇侠传这类 MMRPG 游戏，不知道你有没有玩过？在这些游戏中，有一个非常重要的功能，那就是人物角色自动寻路。当人物处于游戏地图中的某个位置的时候，我们用鼠标点击另外一个相对较远的位置，人物就会自动地绕过障碍物走过去。玩过这么多游戏，不知你是否思考过，这个功能是怎么实现的呢？

算法解析实际上，这是一个非常典型的搜索问题。人物的起点就是他当下所在的位置，终点就是鼠标点击的位置。我们需要在地图中，找一条从起点到终点的路径。这条路径要绕过地图中所有障碍物，并且看起来要是一种非常聪明的走法。所谓“聪明”，笼统地解释就是，走的路不能太绕。理论上讲，最短路径显然是最聪明的走法，是这个问题的最优解。

不过，如果图非常大，那 Dijkstra 最短路径算法的执行耗时会很多。在真实的软件开发中，我们面对的是超级大的地图和海量的寻路请求，算法的执行效率太低，这显然是无法接受的。

实际上，像出行路线规划、游戏寻路，这些真实软件开发中的问题，一般情况下，我们都不需要非得求最优解（也就是最短路径）。在权衡路线规划质量和执行效率的情况下，我们只需要寻求一个次优解就足够了。那如何快速找出一条接近于最短路线的次优路线呢？

这个快速的路径规划算法，就是我们今天要学习的 A* 算法。实际上，A* 算法是对 Dijkstra 算法的优化和改造。

Dijkstra 算法有点儿类似 BFS 算法，它每次找到跟起点最近的顶点，往外扩展。这种往外扩展的思路，其实有些盲目。为什么这么说呢？我举一个例子来给你解释一下。下面这个图对应一个真实的地图，每个顶点在地图中的位置，我们用一个二维坐标（x，y）来表示，其中，x 表示横坐标，y 表示纵坐标。

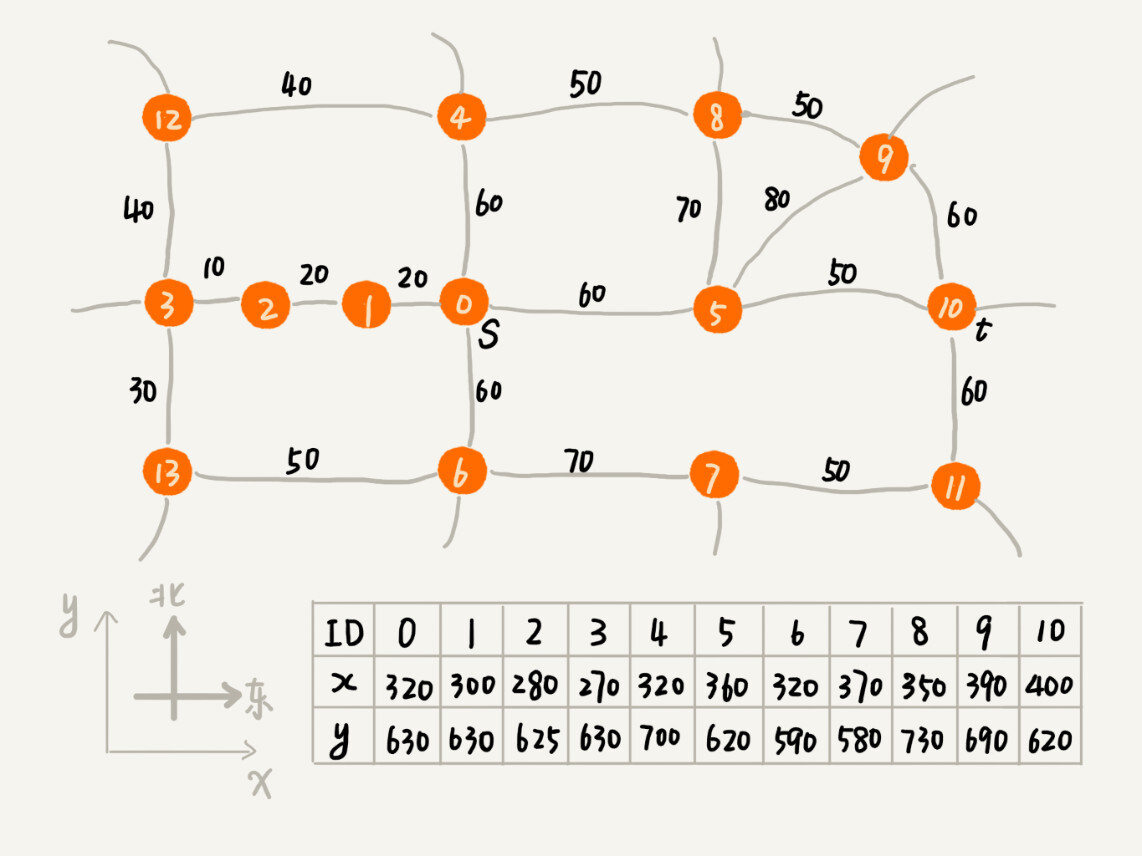
在 Dijkstra 算法的实现思路中，我们用一个优先级队列，来记录已经遍历到的顶点以及这个顶点与起点的路径长度。顶点与起点路径长度越小，就越先被从优先级队列中取出来扩展，从图中举的例子可以看出，尽管我们找的是从 s 到 t 的路线，但是最先被搜索到的顶点依次是 1，2，3。通过肉眼来观察，这个搜索方向跟我们期望的路线方向（s 到 t 是从西向东）是反着的，路线搜索的方向明显“跑偏”了。

之所以会“跑偏”，那是因为我们是按照顶点与起点的路径长度的大小，来安排出队列顺序的。与起点越近的顶点，就会越早出队列。我们并没有考虑到这个顶点到终点的距离，所以，在地图中，尽管 1，2，3 三个顶点离起始顶点最近，但离终点却越来越远。

如果我们综合更多的因素，把这个顶点到终点可能还要走多远，也考虑进去，综合来判断哪个顶点该先出队列，那是不是就可以避免“跑偏”呢？当我们遍历到某个顶点的时候，从起点走到这个顶点的路径长度是确定的，我们记作 g(i)（i 表示顶点编号）。但是，从这个顶点到终点的路径长度，我们是未知的。虽然确切的值无法提前知道，但是我们可以用其他估计值来代替。

这里我们可以通过这个顶点跟终点之间的直线距离，也就是欧几里得距离，来近似地估计这个顶点跟终点的路径长度（注意：路径长度跟直线距离是两个概念）。我们把这个距离记作 h(i)（i 表示这个顶点的编号），专业的叫法是启发函数（heuristic function）。因为欧几里得距离的计算公式，会涉及比较耗时的开根号计算，所以，我们一般通过另外一个更加简单的距离计算公式，那就是曼哈顿距离（Manhattan distance）。曼哈顿距离是两点之间横纵坐标的距离之和。计算的过程只涉及加减法、符号位反转，所以比欧几里得距离更加高效。

原来只是单纯地通过顶点与起点之间的路径长度 g(i)，来判断谁先出队列，现在有了顶点到终点的路径长度估计值，我们通过两者之和 f(i)=g(i)+h(i)，来判断哪个顶点该最先出队列。综合两部分，我们就能有效避免刚刚讲的“跑偏”。这里 f(i) 的专业叫法是估价函数（evaluation function）。从刚刚的描述，我们可以发现，A* 算法就是对 Dijkstra 算法的简单改造。实际上，代码实现方面，我们也只需要稍微改动几行代码，就能把 Dijkstra 算法的代码实现，改成 A* 算法的代码实现。

在 A* 算法的代码实现中，顶点 Vertex 类的定义，跟 Dijkstra 算法中的定义，稍微有点儿区别，多了 x，y 坐标，以及刚刚提到的 f(i) 值。

A* 算法的代码实现的主要逻辑是下面这段代码。它跟 Dijkstra 算法的代码实现，主要有 3 点区别：

  • 优先级队列构建的方式不同。A* 算法是根据 f 值（也就是刚刚讲到的 f(i)=g(i)+h(i)）来构建优先级队列，而 Dijkstra 算法是根据 dist 值（也就是刚刚讲到的 g(i)）来构建优先级队列；
  • A* 算法在更新顶点 dist 值的时候，会同步更新 f 值；循环结束的条件也不一样。
  • Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。

注：

本文中的所有图均来自于极客时间《数据结构与算法之美》一课