树状数组及其应用

简介

树状数组（Binary Indexed Tree，简称BIT），有时也被称作Fenwick树，是一种用于高效处理前缀和、区间求和、以及相应更新等问题的数据结构。它提供了比普通数组更好的方法来实现这些操作，特别是在需要频繁更新元素和查询前缀和的场景中。树状数组在时间复杂度和空间复杂度上都很优秀，实现也相对简单。

普通树状数组维护的信息及运算要满足 结合律 且 可差分，如加法（和）、乘法（积）、异或等。

• 结合律：$(x \circ y) \circ z = x \circ (y \circ z)$，其中$\circ$ 是一个二元运算符。

• 可差分：具有逆运算的运算，即已知$x \circ y$ 和 x 可以求出 y。

事实上，树状数组能解决的问题是线段树能解决的问题的子集：树状数组能做的，线段树一定能做；线段树能做的，树状数组不一定可以。然而，树状数组的代码要远比线段树短，时间效率常数也更小，因此仍有学习价值。

有时，在差分数组和辅助数组的帮助下，树状数组还可解决更强的 区间加单点值 和 区间加区间和 问题。

使用场景举例

先来举个例子：我们想知道$a[1 \ldots 7]$ 的前缀和，怎么做？

一种做法是：$a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7$，需要求 7 个数的和。

但是如果已知三个数 A，B，C，$A = a[1 \ldots 4]$ 的和，$B = a[5 \ldots 6]$ 的总和，$C = a[7 \ldots 7]$ 的总和（其实就是 a[7] 自己）。你会怎么算？你一定会回答：A + B + C，只需要求 3 个数的和。

这就是树状数组能快速求解信息的原因：我们总能将一段前缀 [1, n] 拆成 不多于$\boldsymbol{\log n}$ 段区间，使得这$\log n$ 段区间的信息是 已知的。

于是，我们只需合并这$\log n$ 段区间的信息，就可以得到答案。相比于原来直接合并 n 个信息，效率有了很大的提高。

不难发现信息必须满足结合律，否则就不能像上面这样合并了。

基本原理

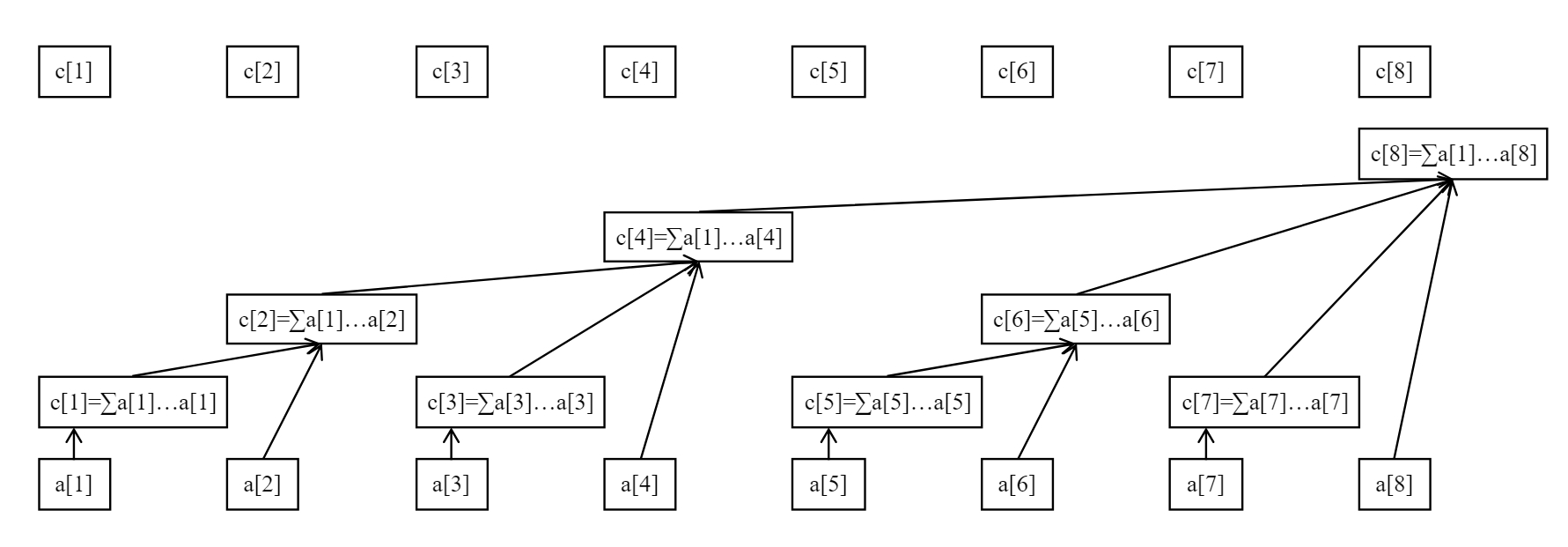
下面这张图展示了树状数组的工作原理：

最下面的八个方块代表原始数据数组 a。上面参差不齐的方块（与最上面的八个方块是同一个数组）代表数组 a 的上级——c 数组。

c 数组就是用来储存原始数组 a 某段区间的和的，也就是说，这些区间的信息是已知的，我们的目标就是把查询前缀拆成这些小区间。

例如，从图中可以看出：

$c_2 管辖的是 a[1 \ldots 2]$；

$c_4 管辖的是 a[1 \ldots 4]；$

$c_6 管辖的是 a[5 \ldots 6]；$

$c_8 管辖的是 a[1 \ldots 8]；$

剩下的 c[x] 管辖的都是 a[x] 自己（可以看做$a[x \ldots x]$ 的长度为 1 的小区间）。
不难发现，c[x] 管辖的一定是一段右边界是 x 的区间总信息。我们先不关心左边界，先来感受一下树状数组是如何查询的。

初步感受

举例：计算$a[1 \ldots 7]$ 的和。

过程：从$c_7$ 开始往前跳，发现$c_7$ 只管辖$a_7$ 这个元素；然后找$c_6$，发现$c_6$ 管辖的是$a[5 \ldots 6]$，然后跳到$c_{4}$，发现$c_4$ 管辖的是$a[1 \ldots 4]$ 这些元素，然后再试图跳到$c_0$，但事实上$c_0$ 不存在，不跳了。

我们刚刚找到的 c 是$c_7, c_6, c_4$，事实上这就是$a[1 \ldots 7]$ 拆分出的三个小区间，合并得到答案是$c_7 + c_6 + c_4$。

举例：计算$a[4 \ldots 7]$ 的和。

我们还是从$c_7$ 开始跳，跳到$c_6$ 再跳到$c_4$。此时我们发现它管理了$a[1 \ldots 4]$ 的和，但是我们不想要$a[1 \ldots 3]$ 这一部分，怎么办呢？很简单，减去$a[1 \ldots 3]$ 的和就行了。

那不妨考虑最开始，就将查询$a[4 \ldots 7]$ 的和转化为查询$a[1 \ldots 7]$ 的和，以及查询$a[1 \ldots 3]$ 的和，最终将两个结果作差。

管辖区间

那么问题来了，c[x]$(x \ge 1)$ 管辖的区间到底往左延伸多少？也就是说，区间长度是多少？

树状数组中，规定 c[x] 管辖的区间长度为$2^{k}$，其中：

设二进制最低位为第 0 位，则 k 恰好为 x 二进制表示中，最低位的 1 所在的二进制位数；
$2^k$（c[x] 的管辖区间长度）恰好为 x 二进制表示中，最低位的 1 以及后面所有 0 组成的数。
举个例子，$c_{88}$ 管辖的是哪个区间？

因为$88_{(10)}=01011000_{(2)}$，其二进制最低位的 1 以及后面的 0 组成的二进制是 1000，即 8，所以$c_{88}$ 管辖 8 个 a 数组中的元素。

因此，$c_{88}$ 代表$a[81 \ldots 88]$ 的区间信息。

我们记 x 二进制最低位 1 以及后面的 0 组成的数为$\operatorname{lowbit}(x)$，那么 c[x] 管辖的区间就是$[x-\operatorname{lowbit}(x)+1, x]$。

索引的二进制表示

树状数组的核心原理基于索引的二进制表示。二进制的每个索引都可以写作若干个2的幂的和。例如，索引11的二进制表示为1011（即2^3 + 2^1 + 2^0），每个位置上的1表示相应的幂次被选中。

最低有效位 LSB

在树状数组中，最低有效位（Least Significant Bit，LSB）定义为从右向左第一个非零位。在计算机中，我们可以用x & (-x)的方式来获取一个数的LSB，这是因为负数在计算机中通常使用补码形式表示，即将正数的二进制表示取反后加一。

例如:

x (正)    = 101100  (二进制，36 的二进制表示)
-x (负)   = 010100  (二进制，-36 的二进制补码表示)
x & (-x)  = 000100  (二进制，LSB)

查询（Query）

接下来我们来看树状数组具体的操作实现，先来看区间查询。

回顾查询$a[4 \ldots 7]$ 的过程，我们是将它转化为两个子过程：查询$a[1 \ldots 7]$ 和查询$a[1 \ldots 3]$ 的和，最终作差。

其实任何一个区间查询都可以这么做：查询$a[l \ldots r]$ 的和，就是$a[1 \ldots r]$ 的和减去$a[1 \ldots l - 1]$ 的和，从而把区间问题转化为前缀问题，更方便处理。

事实上，将有关$l \ldots r$ 的区间询问转化为$1 \ldots r$ 和$1 \ldots l - 1$ 的前缀询问再差分，在竞赛中是一个非常常用的技巧。

那前缀查询怎么做呢？回顾下查询$a[1 \ldots 7]$ 的过程：

从$c_{7}$ 往前跳，发现$c_{7}$ 只管辖$a_{7}$ 这个元素；然后找$c_{6}$，发现$c_{6}$ 管辖的是$a[5 \ldots 6]$，然后跳到$c_{4}$，发现$c_{4}$ 管辖的是$a[1 \ldots 4]$ 这些元素，然后再试图跳到$c_0$，但事实上$c_0$ 不存在，不跳了。

我们刚刚找到的 c 是$c_7, c_6, c_4$，事实上这就是$a[1 \ldots 7]$ 拆分出的三个小区间，合并一下，答案是$c_7 + c_6 + c_4$。

观察上面的过程，每次往前跳，一定是跳到现区间的左端点的左一位，作为新区间的右端点，这样才能将前缀不重不漏地拆分。比如现在$c_6$ 管的是$a[5 \ldots 6]$，下一次就跳到 5 - 1 = 4，即访问$c_4$。

我们可以写出查询$a[1 \ldots x]$ 的过程：

1. 从 c[x] 开始往前跳，有 c[x] 管辖$a[x-\operatorname{lowbit}(x)+1 \ldots x]$；

2. 令$x \gets x - \operatorname{lowbit}(x)$，如果 x = 0 说明已经跳到尽头了，终止循环；否则回到第一步。

3. 将跳到的 c 合并。

树状数组与其树形态的性质

在讲解单点修改之前，先讲解树状数组的一些基本性质，以及其树形态来源，这有助于更好理解树状数组的单点修改。

我们约定：

1. $l(x) = x - \operatorname{lowbit}(x) + 1$。即，l(x) 是 c[x] 管辖范围的左端点。

2. 对于任意正整数 x，总能将 x 表示成$s \times 2^{k + 1} + 2^k$ 的形式，其中$\operatorname{lowbit}(x) = 2^k$。

3. 下面「c[x] 和 c[y] 不交」指 c[x] 的管辖范围和 c[y] 的管辖范围不相交，即 [l(x), x] 和 [l(y), y] 不相交。「c[x] 包含于 c[y]」等表述同理。

性质1：对于$\boldsymbol{x \le y}$，要么有$\boldsymbol{c[x]}$ 和$\boldsymbol{c[y]}$ 不交，要么有$\boldsymbol{c[x]}$ 包含于$\boldsymbol{c[y]}$。

性质2：在$\boldsymbol{c[x]}$ 真包含于$\boldsymbol{c[x + \operatorname{lowbit}(x)]}$。

性质3：对于任意$\boldsymbol{x < y < x + \operatorname{lowbit}(x)}$，有$\boldsymbol{c[x]}$ 和$\boldsymbol{c[y]}$ 不交。

有了这三条性质的铺垫，我们接下来看树状数组的树形态（请忽略 a 向 c 的连边）。

事实上，树状数组的树形态是 x 向$x + \operatorname{lowbit}(x)$ 连边得到的图，其中$x + \operatorname{lowbit}(x)$ 是 x 的父亲。

注意，在考虑树状数组的树形态时，我们不考虑树状数组大小的影响，即我们认为这是一棵无限大的树，方便分析。实际实现时，我们只需用到$x \le n$ 的 c[x]，其中 n 是原数组长度。

更新（Update）

我们通过将LSB加到索引上，从某个节点向上遍历，更新所有包含该节点的区间和。例如，如果我们想要在索引3（二进制011）处加上一个数，那么我们首先将其加到3，然后索引加LSB变为4（二进制100），接着变为8（二进制1000），直到索引超出数组长度为止。

代码实现

class FenwickTree {
  constructor(size) {
    this.size = size;
    this.tree = new Array(size + 1).fill(0);
  }

  // LSB计算
  LSB(i) {
    return i & (-i);
  }

  // 在i位置增加值val
  update(i, val) {
    while (i <= this.size) {
      this.tree[i] += val;
      i += this.LSB(i);
    }
  }

  // 查询前缀和
  query(i) {
    let sum = 0;
    while (i > 0) {
      sum += this.tree[i];
      i -= this.LSB(i);
    }
    return sum;
  }

  // 查询区间[l, r]的和
  queryRange(l, r) {
    return this.query(r) - this.query(l - 1);
  }
}

实战举例

https://leetcode.cn/problems/distribute-elements-into-two-arrays-ii/description/?envType=daily-question&envId=2024-06-05

class BinaryIndexedTree {
  constructor(n) {
    this.tree = new Array(n + 1).fill(0);
  }

  add(i) {
    while (i < this.tree.length) {
      this.tree[i]++;
      i += i & -i;
    }
  }

  get(i) {
    let sum = 0;
    while (i > 0) {
      sum += this.tree[i];
      i -= i & -i;
    }
    return sum;
  }
}

var resultArray = function(nums) {
  const n = nums.length;
  const sortedNums = [...nums].sort((a, b) => a - b);
  const index = {};
  // index中存储的是key对应的值在nums数组中排第几
  for (let i = 0; i < n; i++) {
    index[sortedNums[i]] = i + 1;
  }

  const arr1 = [nums[0]];
  const arr2 = [nums[1]];
  const tree1 = new BinaryIndexedTree(n);
  const tree2 = new BinaryIndexedTree(n);
  tree1.add(index[nums[0]]);
  tree2.add(index[nums[1]]);

  for (let i = 2; i < n; i++) {
    // index[nums[i]]表示的是nums[i]在nums数组中排第几
    // tree1.get(index[nums[i]])获取的是，arr1数组中，比nums[i]小的有几个
    // count1就是arr1数组中，比nums[i]严格大的有几个
    const count1 = arr1.length - tree1.get(index[nums[i]]);
    const count2 = arr2.length - tree2.get(index[nums[i]]);
    if (count1 > count2 || (count1 === count2 && arr1.length <= arr2.length)) {
      arr1.push(nums[i]);
      tree1.add(index[nums[i]]);
    } else {
      arr2.push(nums[i]);
      tree2.add(index[nums[i]]);
    }
  }

  return arr1.concat(arr2);
};

作者：力扣官方题解
链接：https://leetcode.cn/problems/distribute-elements-into-two-arrays-ii/solutions/2796537/jiang-yuan-su-fen-pei-dao-liang-ge-shu-z-d5mh/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。