系统结构的矩阵表达
邻接矩阵
邻接矩阵A是表达系统间要素基本二元关系或直接联系情况的方阵。若A=(aij)n×n,则其定义式为:
aij={1,SiRSj(Si对Sj有某种二元关系)0,SiRˉSj(Si对Sj没有某种二元关系)
假设有如下邻接矩阵
A=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0000000100000000010000000110000000000010000100000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
在邻接矩阵中,若有一列(如第j列)元素全为0,则第j个元素是系统的输入元素;若有一行(如第i行)元素全为0,则第i个元素是输出元素。
可达矩阵
若在要素Si和Sj 之间存在某种传递性二元关系,则称Si是可以到达Sj的。
所谓可达矩阵M,就是表明系统要素之间任意次传递性二元关系或有向图上两个节点之间通过任意长的路径可以到达情况的方阵。
若M=(mij)n×n,且在无回路条件下的最大路长或传递次数为r,即0≤t≤r,则可达矩阵的定义式为:
mij={1,SiRtSj,(存在从i至j的路长最大为r的通路),0,SiRˉtSj,(不存在从i至j的通路)
当t=1时,表示基本的二元关系,M即为A,当t=0时,表示Si 自身到达,也称反射性的二元关系,当t≥2 时,表示传递性二元关系。
矩阵A和M的元素均为1或0,是n×n 阶的0-1矩阵,且符合布尔代数的运算规则,即0+0=0,0+1=1,1+0=1,1+1=1,0×0=0,0×1=0,1×0=0,1×1=1
通过对邻接矩阵A的运算,可求出系统要素的可达矩阵M,其计算公式为:
M=(A+I)r
其中I为与A同阶的单位矩阵(其主对角线元素全为1,其他都为0,反应要素自身零步到达自身);r为最大传递次数。
以刚才的邻接矩阵为例,
A+I=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1000000110000000110000001110000010000010100100001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
在此基础上,我们继续计算通过两步的到达情况
(A+I)2=A2+A+I=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡100000011000000011①①0000101100001000001①10①100001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
其中①表示要素间通过两步到达的情况,其中展开平方公式时利用了I2=I(矩阵运算结果),A+A=A (布尔代数) ,其实这里也可以直接先求出M再直接用矩阵乘法的计算法则,只是注意求mij 的时候要用布尔代数。
进一步计算发现(A+I)3=(A+I)2,那么说明r=2,即最大传递次数为2时,就找到了所有的可达关系,因此
M=(A+I)2=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1000000110000000111100001011000010000011101100001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
其他矩阵
缩减矩阵
根据强连接要素的可替换性,在已有的可达矩阵M中,将具有强连接关系的一组要素看作一个要素,保留其中的某个代表,删除其余要素及其在M中的行和列,即可得到该可达矩阵M的缩减矩阵M’,具体什么是强连接元素,后续简化过程中会提到
骨架矩阵
对于给定系统,A的可达矩阵M是唯一的,但实现某一可达矩阵M的的邻接矩阵A可以有多个。把实现某一可达矩阵M,具有最小二元关系个数(1的个数)的邻接矩阵叫做M的最小二元关系矩阵,或叫做骨架矩阵,记作A’
如何简化:建立递阶结构模型的规范方法
建立反应系统问题要素见层次关系的递阶结构模型,可在可达矩阵M的基础上进行,一般要经过四个步骤:区域划分,级位划分,骨架矩阵提取,多级递阶有向图绘制。
区域划分
区域划分是将系统的构成要素集合S分成关于给定二元关系R的相互独立的区域的过程。
为此,需要首先以可达矩阵M为基础,划分与要素相关联的系统要素的类型,并找出在整个系统中有明显特征的要素,有关要素集合的定义如下:
(1)可达集R(Si),系统要素Si 的可达集是在可达矩阵中由Si 可到达的诸要素所构成的集合,其定义式为
R(Si)={Sj∣Sj⊂S,mij=1,j=1,2,…,n}
在给出的可达矩阵中有
R(S1)={S1}R(S2)={S1,S2}R(S3)={S3,S4,S5,S6}R(S4)=R(S6)={S4,S5,S6}R(S5)={S5}R(S7)={S1,S2,S7}
(2)先行集A(Si)。系统要素Si 的先行集是在可达矩阵中可达到Si 的诸要素的集合,其定义式为:
A(Si)={Sj∣Sj⊂S,mji=1,j=1,2,…,n}
在给出的可达矩阵中有
A(S1)={S1,S2,S7}A(S2)={S2,S7}A(S3)={S3}A(S4)=A(S6)={S3,S4,S6}A(S5)={S3,S4,S5,S6}A(S7)={S7}
(3)共同集C(Si),系统要素Si 的共同集是Si 的可达集和先行集的交集,其定义式为:
C(Si)={Sj∣Sj⊂S,mij=1,mji=1,j=1,2,…,n}
在给出的可达矩阵中有
C(S1)={S1}C(S2)={S2}C(S3)={S3}C(S4)=C(S6)={S4,S6}C(S5)={S5}C(S7)={S7}
(4)起始集B(S)和终止集E(S)。系统要素集合S的起始集实在S中只影响(到达)其他要素而不受其他要素影响的要素构成的集合。系统要素集合S的终止集是在S中,只受其他要素影响而不影响其他要素的要素的集合。
起始集的定义式如下:
B(S)={Si∣Si⊂S,C(Si)=A(Si),i=1,2,…,n}
这个定义的意思是,如果Si 是起始集中的元素,则其先行集是可达集的子集,也就是说任何可达Si 的元素,都可以由Si 到达
之前的可达矩阵的起始集B={S3,S7}
终止集的定义式如下:
E(S)={Si∣Si⊂S,C(Si)=R(Si),i=1,2,…,n}
这个定义的意思是,如果Si 是终止集中的元素,则其可达集是先行集集的子集,也就是说任何Si 可达的元素,都可以到达Si
这样,要区分系统要素集合S是否可分割,只要研究系统起始集B中的要素及其可达集元素能否分割,或者研究终止集及其先行集要素是否可分割
利用起始集B判断区域是否可以划分的规则如下:
在B中任取两个元素bu,bv:
- 如果R(bu)∩R(bv)=∅,则bu,bv以及R(bu),R(bv) 中的要素属于同一区域,若对所有u,v都有此结果,则区域不可分
- 如果R(bu)∩R(bv)=∅,则bu,bv 以及R(bu),R(bv) 中的要素不属于同一区域,若对所有u,v都有此结果,则S至少可以被划分为两个区域
区域划分的结果可记为:II(S)=P1,P2,…Pm,经过区域划分后的可达矩阵是一个块对角矩阵(记作M(P))
因为B={S3,S7},且有R(S3)∩R(S7)=∅,所以S3,S4,S5,S6 和S1,S2,S7 分属两个相对独立的区域,即有II(S)=P1,P2={S3,S4,S5,S6},{S1,S2,S7}
此时的可达矩阵M变为如下块对角矩阵M(P)
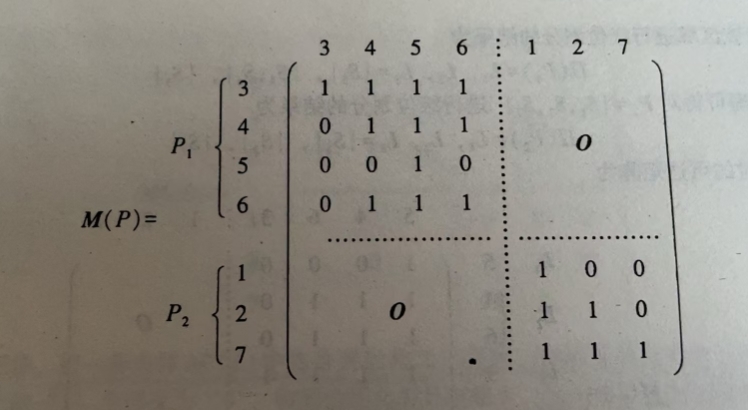
级位划分
区域内的级位划分,即确定某区域内各要素所处的层次地位,这是建立多级递阶结构模型的关键。
设P是有区域划分得到的某区域的要素集合,若用L1,L2,…,Ll 表示从高到低的各级要素集合,则级位划分结果可记为II(P)=L1,L2,…,Ll
某系统要素集合的最高级要素即该系统的终止集要素。级位划分的基本做法为,找出整个系统要素集合的最高级要素(终止集要素)后,可将他们去掉,再求剩余要素集合的最高级要素,以此类推,直到求道最低一级要素集合(即Ll)
为此,令L0=∅,最高级要素为L1,没有零级元素,则有:
L1={Si∣Si⊂P−L0,C0(Si)=R0Si,i=1,2,…n}L2={Si∣Si⊂P−L0−L1,C1(Si)=R1Si,i≤n}...Lk={Si∣Si⊂P−L0−L1−…−Lk−1,Ck−1(Si)=Rk−1Si,i≤n}
对P1={S3,S4,S5,S6} 进行级位划分的过程如下所示
| 要素合集 | Si | R(Si) | A(Si) | C(Si) | C(Si)=R(Si) | II(P1) |
|---|
| P1−L0 | 3456 | 3,4,5,64,5,654,5,6 | 33,4,63,4,5,63,4,6 | 34,654,6 | falsefalsetruefalse | L1={S5} |
| P1−L0−L1 | 346 | 3,4,64,64,6 | 33,4,63,4,6 | 34,64,6 | falsetruetrue | L2={S4,S6} |
| P1−L0−L1−L2 | 3 | 3 | 3 | 3 | true | L3={S3} |
同理可对P2 进行级位划分,划分后的可达矩阵为:
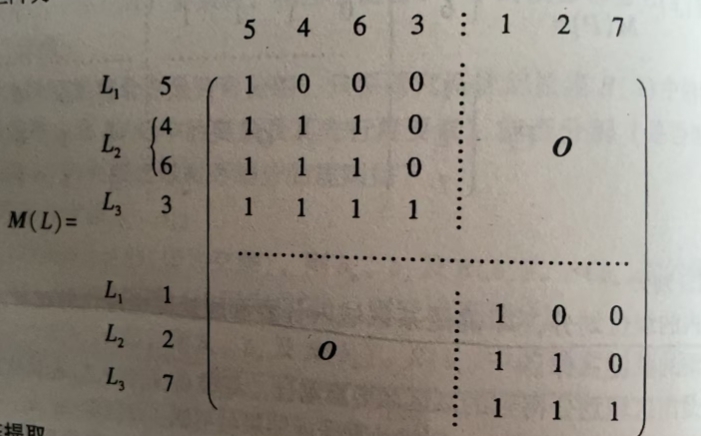
骨架矩阵提取
对可达矩阵M(L)的缩约和检出,建立起M(L)的最小实现矩阵,即骨架矩阵A’。这里的股价矩阵,也就是M的最小实现多级递阶结构矩阵
主要步骤有以下三步:
第一步,检查各层次中的强连接要素,建立可达矩阵M(L)的缩减矩阵M’(L),对例子中的强连接要素集合{S4,S6}做缩减处理,这里以S4为代表

第二步,去掉M’(L)中已具有邻接二元关系的要素间的越级二元关系,得到进一步简化后的新矩阵M’'(L)
在例子中,以后第二级要素(S4,S2) 到第一级元素(S5,S1),和第三级要素(S3,S7) 到第二集元素的邻接二元关系,所以可以去掉第三级元素到第一集元素的越级二元关系
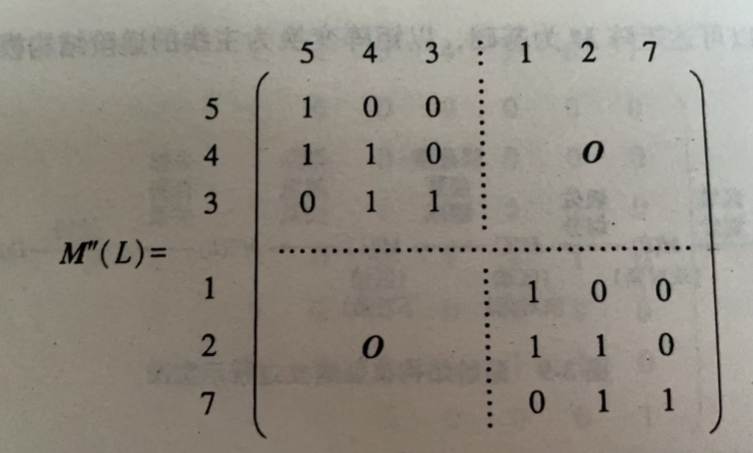
第三步:去掉M’‘(L)中的自身到达的二元关系,即减去单位矩阵,得到经过简化后具有最小二元关系个数的骨架矩阵A’
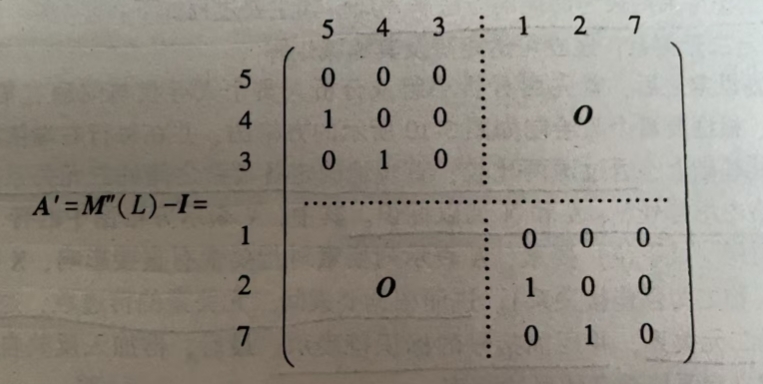
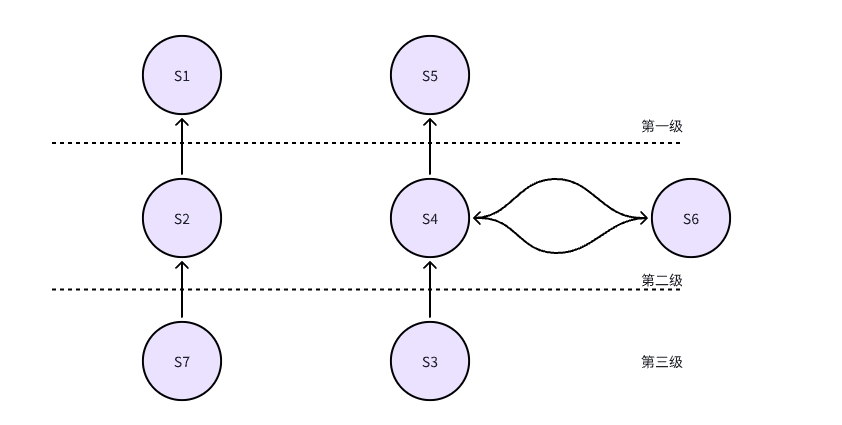
多级递阶有向图绘制
根据骨架矩阵A’,绘制多级递阶有向图D的步骤一般有三步:
第一步:分区域从上到下逐级排列系统构成要素
第二步:同级加入被删除的要素,如例子中和S4强相关的S6
第三步:按A’所示的邻接二元关系,用有向弧绘制